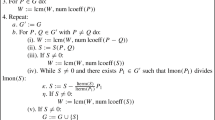Algebraic independence of elementary functions and its application to Masser's vanishing theorem

Summary

Here is an improvement on Masser's Refined Identity (D. W. Masser:A vanishing theorem for power series. Invent. Math.67 (1982), 275–296). The present method depends on a result from differential algebra andp-adic analysis. The investigation from the viewpoint ofp-adic analysis makes the proof clearer and, in particular, it is possible to exclude the concept of “density” which is necessary in Masser's treatment. That is to say, the theorem will be stated as follows: Let Ω = (ω _ij ) be a nonsingular matrix inM _n (ℤ) with no roots of unity as eigenvalue. LetP(z) be a nonzero polynomial inC[z],z = (z ₁,⋯,z _n ). Letx = (x ₁,⋯,x _n ) be an element ofC ⁿ withx _i ≠ 0 for eachi. Define

$$\Omega x = \left( {\prod\limits_{i = 1}^n {x_i^{\omega 1_i } ,...,} \prod\limits_{i = 1}^n {x_i^{\omega _{ni} } } } \right)$$

. IfP(Ω^k x) = 0 for infinitely many positive integersk, thenx ₁,⋯,x _n are multiplicatively dependent.

To prove this, the following fact on elementary functions will be needed: LetK be an ordinary differential field andC be its field of constants. LetR be a differential field extension ofK andu ₁,⋯,u _m be elements ofR such that the field of constants ofR is the same asC and for eachi the field extensionK _i =K(u ₁,⋯,u _i ) ofK is a differential one such thatu′ _i =t′ _i−1 u _i for somet _i−1∈K _i−1 oru _i is algebraic overK _i−1. Letf ₁,⋯,f _n ∈R be distinct elements moduloC and suppose that for eachi there is a nonzeroe _i ∈R withe′ _i =f′ _i e _i . Thene ₁,⋯,e _n are linearly independent overK.