Abstract
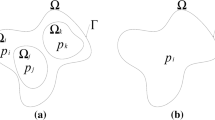
In this paper we consider the stationary problem for a reaction-diffusion system of activator-inhibitor type, which models biological pattern formation, in an axially symmetric domain. It is shown that the system has multi-peak stationary solutions such that the activator is localized around some boundary points if the activator diffuses very slowly and the inhibitor diffuses rapidly enough.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
H. Berestycki, T. Gallouët and O. Kavian, Equations de champs scalaires euclidiens nonlinéaires dans le plan. C. R. Acad. Sci. Paris, Série I Math.,297 (1983), 307–310.
C.-C. Chen and C.-S. Lin, Uniqueness of the ground state solution of δu+f(u)=0 in ℝn,n≥3. Comm. Partial Differential Equations,16 (1991), 1549–1572.
B. Gidas, W.-M. Ni and L. Nirenberg, Symmetry of positive solutions of nonlinear elliptic equations inR n Adv. Math. Suppl. Stud.,7A (1981), 369–402.
A. Gierer and H. Meinhardt, A theory of biological pattern formation. Kybernetik (Berlin),12 (1972), 30–39.
D. Gilbarg and N. S. Trudinger, Elliptic Partial Differential Equations of Second Order. Second Edition. Springer-Verlag, Berlin-Heidelberg-New York-Tokyo, 1983.
J. P. Keener, Activators and inhibitors in pattern formation. Stud. Appl. Math.,59 (1978), 1–23.
M. K. Kwong, Uniqueness of positive solutions of °u−u+u p=0 in ℝn. Arch. Rational Mech. Anal.,105 (1991), 243–266.
M. K. Kwong and L. Zhang, Uniqueness of the positive solutions of °u+f(u)=0 in an annulus. Differential Integral Equations,4 (1991), 583–599.
C.-S. Lin, W.-M. Ni and I. Takagi, Large amplitude stationary solutions to a chemotaxis system. J. Differential Equations,72 (1988), 1–27.
K. McLeod, Uniqueness of positive radial solutions of °u+f(u)=0 inR n, II. Preprint.
Y. Mimura, M. Tabata and Y. Hosono, Multiple solutions of two-point boundary value problems of Neumann type with a small parameter. SIAM J. Math. Anal.,11 (1981), 613–631.
W.-M. Ni and I. Takagi, On the Neumann problem for some semilinear elliptic equations and systems of activator-inhibitor type. Trans. Amer. Math. Soc.,297 (1986), 351–368.
W.-M. Ni and I. Takagi, On the shape of least-energy solutions to a semilinear Neumann problem. Comm. Pure Appl. Math.,44 (1991), 819–851.
W.-M. Ni and I. Takagi, Locating the peaks of least-energy solutions to a semilinear Neumann problem. Duke Math. J.,70 (1993), 247–281.
Y. Nishiura, Global structure of bifurcating solutions of some reaction-diffusion systems. SIAM J. Math. Anal.,13 (1982), 555–593.
Y. Nishiura and H. Fujii, Stability of singularly perturbed solutions to systems of reaction-diffusion equations. SIAM J. Math. Anal.,18 (1987), 1726–1770.
K. Sakamoto, Construction and stability analysis of transition layer solutions in reaction-diffusion systems. Tôhoku Math. J.,42 (1990), 17–44.
W. A. Strauss, Existence of solitary waves in higher dimensions. Comm. Math. Phys.,55 (1977), 149–162.
I. Takagi, Point-condensation for a reaction-diffusion system. J. Differential Equations,61 (1986), 208–249.
Author information
Authors and Affiliations
About this article
Cite this article
Ni, WM., Takagi, I. Point condensation generated by a reaction-diffusion system in axially symmetric domains. Japan J. Indust. Appl. Math. 12, 327–365 (1995). https://doi.org/10.1007/BF03167294
Received:
Issue Date:
DOI: https://doi.org/10.1007/BF03167294