Skip to main content
SpringerLink
Log in

Bifurcation From Stability to Instability for a Free Boundary Problem Arising in a Tumor Model

  • Published:
Archive for Rational Mechanics and Analysis Aims and scope Submit manuscript

Abstract

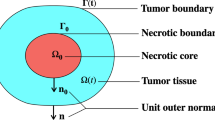
We consider a time-dependent free boundary problem with radially symmetric initial data: σ t − Δσ + σ = 0 if and σ(r,0)=σ0(r) in {r < R(0)} where R(0) is given. This is a model for tumor growth, with nutrient concentration (or tumor cells density) σ(r,t) and proliferation rate then there exists a unique stationary solution (σ S (r), R S ), where R S depends only on the number . We prove that there exists a number μ *, such that if μ < μ * . . . then the stationary solution is stable with respect to non-radially symmetric perturbations, whereas if μ > μ * then the stationary solution is unstable.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Abramowitz, M., Stedgun, I.A.: Handbook of mathematical functions with formulas, graphs, and mathematical tables. Wiley-Interscience Publication, New York, 1972

  2. Adam, J.A.: General aspect of modeling tumor growth and immune response. A Survey of Models for Tumor-Immune System Dynamics. Adam, J.A., Bellomo, N. (ed.), Birkhäuser, Boston, pp. 14–87, 1996

  3. Adam, J.A., Maggelakis, S.A.: Diffusion regulated growth characteristics of a spherical prevascular carcinoma. Bull. Math. Biol. 52, 549–582 (1990)

    Article  MATH  Google Scholar 

  4. Bazaliy, B.V., Friedman, A.: A free boundary problem for elliptic-parabolic system: application to a model of tumor growth. Comm. Partial Differential Equations. 28, 517-560, (2003)

    Article  MATH  MathSciNet  Google Scholar 

  5. Bazaliy, B.V., Friedman, A.: Global existence and asymptotic stability for an elliptic-parabolic free boundary problem: an application to a model of tumor growth. Indiana Univ. Math. J. 52, 1265–1304, (2003)

    Article  MATH  MathSciNet  Google Scholar 

  6. Britton, N., Chaplain, M.A.J.: A qualitative analysis of some models of tissue growth. Math. Biosci. 113, 77–89 (1993)

    Article  MATH  Google Scholar 

  7. Byrne, H.M.: The importance of intercellular adhesion in the development of carcinomas. IMA J. Math. Appl. Med. Biol. 14, 305–323 (1997)

    MATH  Google Scholar 

  8. Byrne, H.M.: A weakly nonlinear analysis of a model of avascular solid tumor growth. J. Math. Biol. 39, 59–89, (1999)

    Article  MATH  MathSciNet  Google Scholar 

  9. Byrne, H.M., Chaplain, M.A.J.: Growth of nonnecrotic tumors in the presence and absence of inhibitors. Math. Biosci. 130, 151–181, (1995)

    Article  MATH  Google Scholar 

  10. Byrne, H.M., Chaplain, M.A.J.: Modelling the role of cell-cell adhesion in the growth and development of carcinomas. Math. Comput. Modelling. 24, 35–55, (1996)

    Article  ADS  MathSciNet  Google Scholar 

  11. Byrne, H.M., Chaplain, M.A.J.: Growth of nonnecrotic tumors in the presence and absence of inhibitors. Math. Biosci. 135, 187–216, (1996)

    Article  ADS  MATH  Google Scholar 

  12. Chaplain, M.A.J.: The development of a spatial pattern in a model for cancer growth. Experimental and Theoretical Advances in Biological Pattern Formation. Othmer, H.G., Maini, P.K., Murray, J.D. (ed.), Plenum Press, 45–60, 1993

  13. Chen, A., Friedman, A.: A free boundary problem for elliptic-hyperbolic system: an application to tumor growth. SIAM J. Math. Anal. 35, 974–986 (2003)

    Article  MATH  MathSciNet  Google Scholar 

  14. Erdelyi, A., Magnus, W., Oberhettinger, F., Tricomi, F.: Higher transcendental functions. Bateman Manuscript, Volume 2, McGraw-Hill, New York, 1953

  15. Fontelos, M., Friedman, A.: Symmetry-breaking bifurcations of free boundary problems in three dimensions. Asymptot. Anal. 35, 187–206, (2003)

    MATH  MathSciNet  Google Scholar 

  16. Fontelos, M., Friedman, A.: Symmetry-breaking bifurcations of chagred drops. Arch. Ration. Mech. Anal. 172, 267–294, (2004)

    Article  MATH  MathSciNet  Google Scholar 

  17. Friedman, A., Reitich, F.: Analysis of a mathematical model for growth of tumor. J. Math. Biol. 38, 262–284, (1999)

    Article  MATH  MathSciNet  Google Scholar 

  18. Friedman, A., Reitich, F.: Symmetry-breaking bifurcation of analytic solutions to free boundary problems: an application to a model of tumor growth. Trans. Amer. Math. Soc. 353, 1587–1634, (2000)

    Article  Google Scholar 

  19. Friedman, A., Reitich, F.: Nonlinear stability of a quasi-static Stefan problem with surface tension: a continuation approach. Ann. Sc. Norm. Super. Pisa Cl. Sci. 30, 341–403, (2001)

    MATH  Google Scholar 

  20. Greenspan, H.P.: Models for the growth of a solid tumor by diffusion. Stud. Appl. Math. 52, 317–340, (1972)

    Google Scholar 

  21. Greenspan, H.P.: On the growth of cell culture and solid tumors. J. Theoret. Biol. 56, 229–242, (1976)

    MathSciNet  Google Scholar 

  22. Maggelakis, S.A., Adam, J.A.: Mathematical model for prevasculat growth of a spherical carcinoma. Math. Comp. Modelling. 13, 23–38, (1990)

    Article  MATH  Google Scholar 

  23. McEwain, D.L.S., Morris, L.E.: Apoptosis as a volume loss mechanism in mathematical models of solid tumor growth. Math. Biosci. 39, 147–157, (1978)

    Article  Google Scholar 

  24. Watson, G.N.: A treatise on the theory of Bessel functions, 2nd edition. Cambridge University Press, Cambridge, 1944

  25. Weinberger, H.F.: The stability of solutions bifurcating from steady or periodic solutions. Dynamical systems (Proc. Internat. Sympos., Univ. Florida, Gainesville, Fla., 1976). Academic Press, New York, 349–366, 1977

Download references

Author information

Authors and Affiliations

  1. Department of Mathematics, The Ohio State University, 231 West 18th Avenue, Columbus, Ohio, 43210, USA

    Avner Friedman

  2. Department of Mathematics, University of Notre Dame, 255 Hurley Hall, Notre Dame, Indiana, 46556

    Bei Hu

Authors
  1. Avner Friedman
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Bei Hu
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Avner Friedman.

Additional information

Communicated by P.H.Rabinowitz

Rights and permissions

Reprints and permissions

About this article

Cite this article

Friedman, A., Hu, B. Bifurcation From Stability to Instability for a Free Boundary Problem Arising in a Tumor Model. Arch. Rational Mech. Anal. 180, 293–330 (2006). https://doi.org/10.1007/s00205-005-0408-z

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00205-005-0408-z

Keywords

Search

Navigation