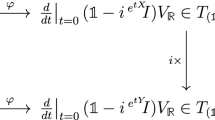Skip to main content
SpringerLink
Log in

The spectral curve of a quaternionic holomorphic line bundle over a 2-torus

  • Published:
manuscripta mathematica Aims and scope Submit manuscript

Abstract

A conformal immersion of a 2-torus into the 4-sphere is characterized by an auxiliary Riemann surface, its spectral curve. This complex curve encodes the monodromies of a certain Dirac type operator on a quaternionic line bundle associated to the immersion. The paper provides a detailed description of the geometry and asymptotic behavior of the spectral curve. If this curve has finite genus the Dirichlet energy of a map from a 2-torus to the 2-sphere or the Willmore energy of an immersion from a 2-torus into the 4-sphere is given by the residue of a specific meromorphic differential on the curve. Also, the kernel bundle of the Dirac type operator evaluated over points on the 2-torus linearizes in the Jacobian of the spectral curve. Those results are presented in a geometric and self contained manner.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Bobenko A.: All constant mean curvature tori in R 3, S 3, H 3 in terms of theta functions. Math. Ann. 290, 209–245 (1991)

    Article  MATH  MathSciNet  Google Scholar 

  2. Bohle, C.: Constrained Willmore tori in the 4-sphere. http://arxiv.org/abs/0803.0633

  3. Bohle, C., Leschke, K., Pedit, F., Pinkall, U.: Conformal maps from a 2-torus to the 4-sphere. http://arxiv.org/abs/0712.2311

  4. Burstall, F., Ferus, D., Leschke, K., Pedit, F., Pinkall, U.: Conformal geometry of surfaces in S 4 and quaternions. Lecture Notes in Mathematics, vol. 1772. Springer, Berlin (2002)

  5. Burstall, F., Pedit, F., Pinkall, U.: Schwarzian derivatives and flows of surfaces. In: Guest, M.A., Miyaoka, R., Ohnita, Y. (eds.) Differential Geometry and Integrable Systems. Contemp. Math., vol. 308, pp. 39–61 (2002)

  6. Dubrovin B.A., Krichever I.M., Novikov S.P.: The Schrödinger equation in a periodic field and Riemann surfaces. Soviet Math. Dokl. 17, 947–952 (1976)

    MATH  Google Scholar 

  7. Feldmann, J., Knörrer, H., Trubowitz, E.: Infinite Genus Riemann Surfaces. AMS (2003)

  8. Ferus D., Leschke K., Pedit F., Pinkall U.: Quaternionic holomorphic geometry: Plücker formula, Dirac eigenvalue estimates and energy estimates of harmonic 2-tori. Invent. Math. 146(3), 507–559 (2001)

    Article  MATH  MathSciNet  Google Scholar 

  9. Grinevich P.G., Schmidt M.U.: Conformal invariant functionals of immersions of tori into R 3. J. Geom. Phys. 26, 51–78 (1998)

    Article  MATH  MathSciNet  Google Scholar 

  10. Hitchin N.: Harmonic maps from a 2-torus to the 3-sphere. J. Differ. Geom. 31(3), 627–710 (1990)

    MATH  MathSciNet  Google Scholar 

  11. Konopelchenko B.G.: Induced surfaces and their integrable dynamics. Stud. Appl. Math. 96, 9–51 (1996)

    MATH  MathSciNet  Google Scholar 

  12. Konopelchenko B.G.: Weierstrass representations for surfaces in 4D spaces and their integrable deformations via DS hierarchy. Ann. Glob. Anal. Geom. 18, 61–74 (2000)

    Article  MATH  MathSciNet  Google Scholar 

  13. Krichever I.: Spectral theory of two-dimensional periodic operators and its applications. Russian Math. Surv. 44, 145–225 (1989)

    Article  MATH  MathSciNet  Google Scholar 

  14. Kuchment P.: Floquet Theory for Partial Differential Equations. Birkhäuser, Basel (1993)

    MATH  Google Scholar 

  15. McIntosh, I.: The quaternionic KP hierarchy and conformally immersed 2-tori in the 4-sphere. http://arxiv.org/abs/0902.3598

  16. Novikov S.P.: Two-dimensional Schrödinger operators in periodic fields. J. Soviet Math. 28, 1–20 (1985)

    Article  MATH  Google Scholar 

  17. Pedit, F., Pinkall, U.: Quaternionic analysis on Riemann surfaces and differential geometry. Doc. Math. J. DMV, Extra Volume ICM Berlin, vol. II, pp. 389–400 (1998)

  18. Pinkall U., Sterling I.: On the classification of constant mean curvature tori. Ann. Math. 130, 407–451 (1989)

    Article  MathSciNet  Google Scholar 

  19. Reed M., Simon B.: Methods of Modern Mathematical Physics, vol. IV. Analysis of Operators. Academic Press, New York (1978)

    Google Scholar 

  20. Schmidt, M.U.: A proof of the Willmore conjecture. http://arxiv.org/abs/math/0203224

  21. Taimanov I.A.: Modified Novikov–Veselov equation and differential geometry of surfaces. Am. Math. Soc. Transl. 179, 133–151 (1997)

    MathSciNet  Google Scholar 

  22. Taimanov I.A.: The Weierstrass representation of closed surfaces in \({\mathbb{R}^3}\). Funct. Anal. Appl. 32, 49–62 (1998)

    Article  MathSciNet  Google Scholar 

  23. Taimanov I.A.: Two-dimensional Dirac operator and surface theory. Russian Math. Surv. 61, 79–159 (2006)

    Article  MATH  MathSciNet  Google Scholar 

  24. Warner F.: Foundations of differentiable manifolds and Lie groups. Scott, Foresman and Co., Glenview, Ill.-London (1971)

    MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Institut für Mathematik, Technische Universität Berlin, Strasse des 17. Juni 136, 10623, Berlin, Germany

    Christoph Bohle & Ulrich Pinkall

  2. Mathematisches Institut der Universität Tübingen, Auf der Morgenstelle 10, 72076, Tübingen, Germany

    Franz Pedit

  3. Department of Mathematics, University of Massachusetts, Amherst, MA, 01003, USA

    Franz Pedit

Authors
  1. Christoph Bohle
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Franz Pedit
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Ulrich Pinkall
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Christoph Bohle.

Additional information

All authors supported by DFG SPP 1154 “Global Differential Geometry”. F. Pedit additionally supported by Alexander von Humboldt foundation.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Bohle, C., Pedit, F. & Pinkall, U. The spectral curve of a quaternionic holomorphic line bundle over a 2-torus. manuscripta math. 130, 311–352 (2009). https://doi.org/10.1007/s00229-009-0288-x

Download citation

  • Received:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00229-009-0288-x

Mathematics Subject Classification (2000)

Search

Navigation