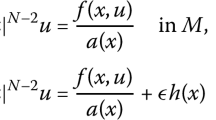Abstract
Let \({\cal M}\) be a connected compact smooth Riemannian manifold of dimension \(n \ge 3\) with or without smooth boundary \(\partial {\cal M}.\) We consider the following singularly perturbed nonlinear elliptic problem on \({\cal M}\)
where \(\Delta_{{\cal M}}\) is the Laplace-Beltrami operator on \({\cal M} \), \(\nu\) is an exterior normal to \(\partial {\cal M}\) and a nonlinearity \(f\) of subcritical growth. For certain \(f,\) there exists a mountain pass solution \(u_\varepsilon\) of above problem which exhibits a spike layer. We are interested in the asymptotic behaviour of the spike layer. Without any non-degeneracy condition and monotonicity of \(f(t)/t,\) we show that if \(\partial {\cal M} =\emptyset(\partial {\cal M} \ne \emptyset),\) the peak point \(x_\varepsilon\) of the solution \(u_\varepsilon\) converges to a maximum point of the scalar curvature \(S\) on \({\cal M}\)(the mean curvature \(H\) on \(\partial {\cal M})\) as \(\varepsilon \to 0,\)respectively.
Similar content being viewed by others
References
Ambrosetti, A., Rabinowitz, P.H.: Dual variational methods in critical point theory and applications. J. Funct. Anal. 14, 349–381 (1973).
Berestycki, H., Lions, P.-L.: Nonlinear scalar field equations. I. Existence of a ground state. Arch. Rational Mech. Anal. 82, 313–345 (1983).
Byeon, J.: Existence of large positive solutions of some nonlinear elliptic equations on singularly perturbed domains. Comm. in P. D. E. 22, 1731–1769 (1997).
Chavel, I.: Eigenvalues in Riemannian Geometry. Academic Press (1984).
Del Pino, M., Felmer, P.L.: Spike-layered solutions of singularly perturbed elliptic problems in a degenerate setting. Indiana Univ. Math. J. 48, 883–898 (1999).
Escobar, F.: Conformal deformation of a Riemannian metric to a scalar flat metric with constant mean curvature on the boundary. Annal. Math. 136, 1–50 (1992).
Gidas, B., Ni, W.N., Nirenberg, L.: Symmetry and related properties via teh maximum principle. Comm. Math. Phys. 68, 209–243 (1979).
Gilbarg, D., Trudinger, N.S.: Elliptic Partial Differential Equations of Second Order; second edition. Grundlehren 224, Springer, Berlin, Heidelberg, New York and Tokyo (1983).
Jeanjean, L., Tanaka, K.: A remark on least energy solutions in R N. Proc. Amer. Math. Soc. 131, 2399–2408 (2003).
Kwong, K.M.: Uniqueness of positive solutions of Δ u−u+u p = 0 in R n. Arch. Rat. Mech. Anal. 105, 243–266 (1989).
Li, Y.Y., Nirenberg, L.: The Dirichlet problem for singularly perturbed elliptic equations. Comm. Pure Appl. Math. 51, 1445–1490 (1998).
Lin, C.S., Ni, W.M., Takagi, I.: Large amplitude stationary solutions to a chemotaxis system. J. Differential Equations 72, 1–27 (1988).
Ni, W.M., Takagi, I.: On the shape of least-energy solutions to a semilinear Neumann problem. Comm. Pure Appl. Math. 44, 819–851 (1991).
Ni, W.M., Takagi, I.: Locating the peaks of least-energy solutions to a semilinear Neumann problem. Duke Math. J. 70, 247–281 (1993).
Ni, W.M., Takagi, I., Yanagida, E.: Stability of least energy patterns of the shadow system for an activator-inhibitor model. Japan J. Indust. Appl. Math. 18, 259–272 (2001).
Ni, W.M., Wei, J.: On the location and profile of spike-layer solutions to singularly perturbed semilinear Dirichlet problems. Comm. Pure Appl. Math. 48, 731–768 (1995).
Protter, M.H., Weinberger, H.F.: Maximum Principles in Differential Equations. Springer-Verlag, New York, Berlin, Heidelberg and Tokyo (1984).
Struwe, M.: Variational Methods; Application to Nonlinear Partial Differential Equations and Hamiltonian Systems. Springer-Verlag (1990).
Wei, J., Winter, M.: Higher-order energy expansions and spike locations. Calculus of Variations and PDE 20, 403–430 (2004).
Author information
Authors and Affiliations
Corresponding author
Additional information
The research of the first author was supported in part by KRF-2002-070-C000005 of Korea Research Foundation.
Rights and permissions
About this article
Cite this article
Byeon, J., Park, J. Singularly perturbed nonlinear elliptic problems on manifolds. Calc. Var. 24, 459–477 (2005). https://doi.org/10.1007/s00526-005-0339-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00526-005-0339-4