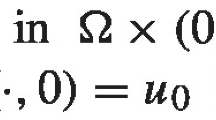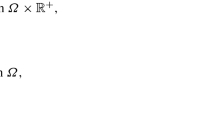Abstract
In this paper, we study the nonlocal ∞-Laplacian type diffusion equation obtained as the limit as p → ∞ to the nonlocal analogous to the p-Laplacian evolution,
We prove exist ence and uniqueness of a limit solution that verifies an equation governed by the subdifferential of a convex energy functional associated to the indicator function of the set \({K = \{ u \in L^2(\mathbb{R}^N) \, : \, | u(x) - u(y)| \le 1, \mbox{ when } x-y \in {\rm supp} (J)\}}\) . We also find some explicit examples of solutions to the limit equation. If the kernel J is rescaled in an appropriate way, we show that the solutions to the corresponding nonlocal problems converge strongly in L ∞(0, T; L 2 (Ω)) to the limit solution of the local evolutions of the p-Laplacian, v t = Δ p v. This last limit problem has been proposed as a model to describe the formation of a sandpile. Moreover, we also analyze the collapse of the initial condition when it does not belong to K by means of a suitable rescale of the solution that describes the initial layer that appears for p large. Finally, we give an interpretation of the limit problem in terms of Monge–Kantorovich mass transport theory.
Similar content being viewed by others
References
Andreu F., Mazón J.M., Rossi J.D., Toledo J.: The Neumann problem for nonlocal nonlinear diffusion equations. J. Evol. Equ. 8, 189–215 (2008)
Andreu F., Mazón J.M., Rossi J.D., Toledo J.: A nonlocal p-Laplacian evolution equation with Neumann boundary conditions. J. Math. Pures Appl. 90(2), 201–227 (2008)
Aronsson G., Evans L.C., Wu Y.: Fast/slow diffusion and growing sandpiles. J. Differ. Equ. 131, 304–335 (1996)
Attouch H.: Familles d’opérateurs maximaux monotones et mesurabilité. Ann. Mat. Pura Appl. 120, 35–111 (1979)
Bates P., Chmaj A.: An integrodifferential model for phase transitions: stationary solutions in higher dimensions. J. Stat. Phys. 95, 1119–1139 (1999)
Bates P., Chmaj A.: A discrete convolution model for phase transitions. Arch. Rat. Mech. Anal. 150, 281–305 (1999)
Bates P., Fife P., Ren X., Wang X.: Travelling waves in a convolution model for phase transitions. Arch. Rat. Mech. Anal. 138, 105–136 (1997)
Benilan, Ph., Crandall, M.G.: Completely accretive operators. In: Clement, Ph., et al. (eds.) Semigroups theory and evolution equations. Marcel Dekker, New York, pp. 41–76 (1991)
Bénilan, Ph., Crandall, M.G., Pazy, A.: Evolution equations governed by accretive operators (2008, in press)
Bénilan Ph., Evans L.C., Gariepy R.F.: On some singular limits of homogeneous semigroups. J. Evol. Equ. 3, 203–214 (2003)
Bourgain, J., Brezis, H., Mironescu, P.: Another look at Sobolev spaces. In: Menaldi, J.L., et al. (eds.) Optimal Control and Partial Differential Equations: A Volume in Honour of A. Bensoussan’s 60th Birthday, pp. 439–455. IOS Press, Amsterdam (2001)
Brezis H.: Équations et inéquations non linéaires dans les espaces vectoriels en dualité. Ann. Inst. Fourier 18, 115–175 (1968)
Brezis H.: Opérateur Maximaux Monotones et Semi-groupes de Contractions dans les Espaces de Hilbert. North-Holland, Amsterdam (1973)
Brezis H., Pazy A.: Convergence and approximation of semigroups of nonlinear operators in Banach spaces. J. Funct. Anal. 9, 63–74 (1972)
Ekeland H.I., Temam R.: Convex Analysis and Variational Problems. North-Holland, Amsterdam (1972)
Carrillo C., Fife P.: Spatial effects in discrete generation population models. J. Math. Biol. 50(2), 161–188 (2005)
Chasseigne E., Chaves M., Rossi J.D.: Asymptotic behaviour for nonlocal diffusion equations. J. Math. Pures Appl. 86, 271–291 (2006)
Chen X.: Existence, uniqueness and asymptotic stability of travelling waves in nonlocal evolution equations. Adv. Differ. Equ. 2, 125–160 (1997)
Cortazar C., Elgueta M., Rossi J.D.: A non-local diffusion equation whose solutions develop a free boundary. Ann. Henri Poincaré 6(2), 269–281 (2005)
Cortazar C., Elgueta M., Rossi J.D., Wolanski N.: Boundary fluxes for non-local diffusion. J. Differ. Equ. 234, 360–390 (2007)
Cortazar C., Elgueta M., Rossi J.D., Wolanski N.: How to approximate the heat equation with Neumann boundary conditions by nonlocal diffusion problems. Arch. Ration. Mech. Anal. 187, 137–156 (2008)
Crandall, M.G.: An introduction to evolution governed by accretive operators. In: Dynamical Systems (Proceedings of the Internatinal Symposium Brown University, Providence, RI, 1974), vol. I, pp. 131–165. Academic Press, New York (1976)
Crandall, M.G.: Nonlinear semigroups and evolution governed by accretive operators. In: Browder, F. (ed.) Proceedings of Symposium in Pure Mathematics, Part I, vol. 45, pp. 305–338. American Mathematical Society, Providence (1986)
Evans, L.C.: Partial differential equations and Monge–Kantorovich mass transfer. Current Developments in Mathematics, 1997 (Cambridge, MA), pp. 65–126. International Press, Boston (1999)
Evans L.C., Feldman M., Gariepy R.F.: Fast/slow diffusion and collapsing sandpiles. J. Differ. Equ. 137, 166–209 (1997)
Evans, L.C., Gangbo, W.: Differential equations methods for the Monge–Kantorovich mass transfer problem. Memories of American Mathematical Society, vol. 137, no. 653 (1999)
Evans L.C., Rezakhanlou Fr.: A stochastic model for growing sandpiles and its continuum limit. Commun. Math. Phys. 197, 325–345 (1998)
Feldman, M.: Growth of a sandpile around an obstacle, Monge Ampère equation: applications to geometry and optimization, (Deerfield Beach, FL, 1997), pp. 55–78, Contemp. Math., vol. 226. American Mathematical Society, Providence (1999)
Fife P.: Some Nonclassical Trends in Parabolic and Parabolic-like Evolutions. Trends in Nonlinear Analysis, pp. 153–191. Springer, Berlin (2003)
Fife P., Wang X.: A convolution model for interfacial motion: the generation and propagation of internal layers in higher space dimensions. Adv. Differ. Equ. 3(1), 85–110 (1998)
Ignat L.I., Rossi J.D.: A nonlocal convection–diffusion equation. J. Funct. Anal. 251, 399–437 (2007)
Mosco U.: Convergence of convex sets and solutions of variational inequalities. Adv. Math. 3, 510–585 (1969)
Villani C.: Topics in optimal transportation. Grad. Stud. Math. 58, 370 (2003)
Author information
Authors and Affiliations
Corresponding author
Additional information
F. Andreu, J. M. Mazón and J. Toledo were supported by the Spanish MEC and FEDER, project MTM2005-00620, and by the project ACOMP2007/112 from Generalitat Valenciana. J. D. Rossi was partially supported by Generalitat Valenciana under AINV2007/03 and ANPCyT PICT 5009, UBA X066 and CONICET (Argentina).
Rights and permissions
About this article
Cite this article
Andreu, F., Mazón, J.M., Rossi, J.D. et al. The limit as p → ∞ in a nonlocal p-Laplacian evolution equation: a nonlocal approximation of a model for sandpiles. Calc. Var. 35, 279–316 (2009). https://doi.org/10.1007/s00526-008-0205-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00526-008-0205-2