Apollonian circle packings: Number theory II. Spherical and hyperbolic packings

Abstract

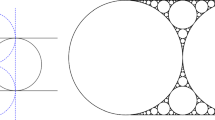
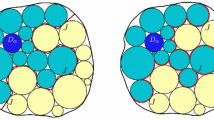
Apollonian circle packings arise by repeatedly filling the interstices between mutually tangent circles with further tangent circles. In Euclidean space it is possible for every circle in such a packing to have integer radius of curvature, and we call such a packing an integral Apollonian circle packing. There are infinitely many different integral packings; these were studied in Part I (J. Number Theory 100, 1–45, 2003). Integral circle packings also exist in spherical and hyperbolic space, provided a suitable definition of curvature is used and again there are an infinite number of different integral packings. This paper studies number-theoretic properties of such packings. This amounts to studying the orbits of a particular subgroup ${\mathcal{A}}$ of the group of integral automorphs of the indefinite quaternary quadratic form $Q_{{\mathcal{D}}}(w,x,y,z)=2(w^{2}+x^{2}+y^{2}+z^{2})-(w+x+y+z)^{2}$ . This subgroup, called the Apollonian group, acts on integer solutions $Q_{{\mathcal{D}}}(w,x,y,z)=k$ . This paper gives a reduction theory for orbits of ${\mathcal{A}}$ acting on integer solutions to $Q_{{\mathcal{D}}}(w,x,y,z)=k$ valid for all integer k. It also classifies orbits for all k≡0 (mod 4) in terms of an extra parameter n and an auxiliary class group (depending on n and k), and studies congruence conditions on integers in a given orbit.