Skip to main content

Advertisement

SpringerLink
Log in

Global stability of an epidemic model for vector-borne disease

  • Published:
Journal of Systems Science and Complexity Aims and scope Submit manuscript

Abstract

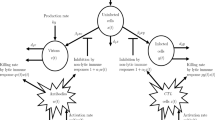
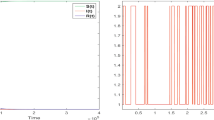
This paper considers an epidemic model of a vector-borne disease which has the vectormediated transmission only. The incidence term is of the bilinear mass-action form. It is shown that the global dynamics is completely determined by the basic reproduction number R 0. If R 0 ≤ 1, the diseasefree equilibrium is globally stable and the disease dies out. If R 0 > 1, a unique endemic equilibrium is globally stable in the interior of the feasible region and the disease persists at the endemic equilibrium. Numerical simulations are presented to illustrate the results.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. WHO, Malaria, 10 fact on Malaria, Available from: http://www.who.int/features/factfiles/malaria/en/index.html, 2009.

  2. CDC, Available from: CDC Dengue Fever homepage, http://www.cdc.gov/ncidod/dvbid/index.htm, 2003.

  3. CDC, West Nile virus update, current case count, Available form: http://www.cdc.gov/ncidod/dvbib/westnile/surv&controlCaseCount03.htm, 2003.

  4. West Nile Virus, Available form: http://www.sfcdcp.org/index.cfm?id=90.

  5. D. J. Rogers, The dynamics of vectors-transmitted diseases in human communities, Phil. Trans. R. Soc. London B, 1998, 321: 513–528.

    Article  Google Scholar 

  6. F. E. Mckenzie, Why model malaria? Parasitol Today, 2000, 16: 511–516.

    Article  Google Scholar 

  7. H. Inaba and H. Sekine, A mathematical model for Chagas disease with infection-age-dependent infectivity, Math. Biosci., 2004, 190: 39–69.

    Article  MathSciNet  MATH  Google Scholar 

  8. Z. Feng, D. L. Smith, F. E. McKenzie, S. A. Levin, Coupling ecology and evolution: Malaria and the S-gene across time scales, Math. Biosci., 2004, 189: 1–19.

    Article  MathSciNet  MATH  Google Scholar 

  9. G. Cruz-Pacheco, L. Esteva, and J. A. Montaño-Hirose, C. Vargas, Modelling the dynamics of West Nile Virus, Bull. Math. Biol., 2005, 67: 1157–1173.

    Article  MathSciNet  Google Scholar 

  10. C. Bowman, A. B. Gumel, P. van den Driessche, J. Wu, and H. Zhu, A mathematical model for assessing control strategies against West Nile virus, Bull. Math. Biol., 2005, 67: 1107–1121.

    Article  MathSciNet  Google Scholar 

  11. E. A. Newton and P. Reiter, A model of the transmission of dengue fever with an evaluation of the impact of ultra-low volume (ULV) insecticide applications on dengue epidemics, Am. J. Trop. Med. Hyg., 1992, 47: 709–720.

    Google Scholar 

  12. L. Esteva and C. Vargas, Analysis of a dengue disease transmission model, Math. Biosci., 1998, 150: 131–151.

    Article  MATH  Google Scholar 

  13. Z. Feng and J. X. Velasco-Hernandez, Competitive exclusion in a vector-host model for the dengue virus, J. Math. Biol., 1997, 35: 523–544.

    Article  MathSciNet  MATH  Google Scholar 

  14. L. Esteva and C. Vargas, A model for dengue disease with variable human population, J. Math. Biol., 1999, 38: 220–236.

    Article  MathSciNet  MATH  Google Scholar 

  15. R. M. Aderson and R. M. May, Population biology of infectious diseases: Part 1, Nature, 1979, 280: 361–368.

    Article  Google Scholar 

  16. H. W. Hethcote, Qualitative analysis of communicable disease models, Math. Biosci., 1976, 28: 335–356.

    Article  MathSciNet  MATH  Google Scholar 

  17. M. Y. Li and J. S. Muldowney, A geometric approach to global-stability problems, SIAM J. Math. Anal., 1996, 27: 1070–1083.

    Article  MathSciNet  MATH  Google Scholar 

  18. J. P. LaSalle, The Stability of Dynamical Systems, SIAM, Philadelphia, PA, 1976.

    MATH  Google Scholar 

  19. G. J. Butler and P. Waltman, Persistence in dynamical systems, J. Differential Equations, 1986, 63: 225–263.

    Article  MathSciNet  Google Scholar 

  20. P. Waltman, A brief survey of persistence, in: S. Busenberg, M. Martelli (Eds.), Delay Differential Equations and Dynamical Systems, Springer, New York, 1991, 31–45.

    Chapter  Google Scholar 

  21. H. I. Freedman, M. X. Tang, and S. G. Ruan, Uniform persistence and flows near a closed positively invariant set, J. Dynam. Diff. Equ., 1994, 6: 583–601.

    Article  MathSciNet  MATH  Google Scholar 

  22. M. Y. Li, J. R. Graef, L. Wang, and J. Karsai, Global dynamics of an SEIR model with a varying total population size, Math. Biosci., 1999, 160: 191–213.

    Article  MathSciNet  MATH  Google Scholar 

  23. R. A. Smith, Some applications of Hausdorff dimension inequalities for orinary differential equations, Proc. R. Soc. Edinburgh A, 1986, 104: 235–251.

    MATH  Google Scholar 

  24. M. Y. Li and J. S. Muldowney, On R. A. Smith’s autonomous convergence theorem, Rocky Mount. J. Math., 1995, 25: 365–379.

    Article  MathSciNet  MATH  Google Scholar 

  25. M. Y. Li and J. S. Muldowney, On Bendixson’s criterion, J. Different. Equ., 1994, 106: 27–39.

    Article  MathSciNet  Google Scholar 

  26. M. W. Hirsch, Systems of differential equations that are competitive or coopertitive. VI: A local C’closing lemma for 3-dimensional systems, Ergod. Theor. Dynam. Sys., 1991, 11: 443–454.

    MathSciNet  MATH  Google Scholar 

  27. C. C. Pugh, Am improved closing lemma and a general density theorem, Am. J. Math., 1967, 89: 1010–1021.

    Article  MathSciNet  MATH  Google Scholar 

  28. C. C. Pugh and C. Robinson, The C 1 closing lemma including Hamiltonians, Ergod. Theor. Dynam. Sys., 1981, 3: 261–313.

    MathSciNet  Google Scholar 

  29. W. A. Coppel, Stability and Asymptotic Behavior of Differential Equations, Heath, Boston, 1965.

  30. R. H. Martin Jr., Logarithmic norms and projections applied to linear differential systems, J. Math. Anal. Appl., 1974, 45: 392–410.

    Article  Google Scholar 

  31. M. Fiedler, Additive compound matrices and inequality for eigenvalues of stochastic matrices, Czech Math. J., 1974, 99: 392–402.

    MathSciNet  Google Scholar 

  32. J. S. Muldowney, Compound matrices and ordinary differential equations, Rocky Mount. J. Math., 1990, 20: 857–872.

    Article  MathSciNet  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Faculty of Science, Xi’an Jiaotong University, Xi’an, 710049, China

    Hongzhi Yang

  2. State Key Laboratory of Multiphase Flow in Power Engineering, Xian Jiaotong University, Xi’an, 710049, China

    Huiming Wei

  3. Department of Mathematics, Xinyang Normal University, Xinyang, 464000, China

    Huiming Wei & Xuezhi Li

Authors
  1. Hongzhi Yang
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Huiming Wei
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Xuezhi Li
    View author publications

    You can also search for this author in PubMed Google Scholar

Additional information

This research is supported by the Natural Science Foundation of China under Grant Nos. 10371105 and 10671166 and the Natural Science Foundation of Henan Province under Grant No. 0312002000.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Yang, H., Wei, H. & Li, X. Global stability of an epidemic model for vector-borne disease. J Syst Sci Complex 23, 279–292 (2010). https://doi.org/10.1007/s11424-010-8436-7

Download citation

  • Received:

  • Revised:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11424-010-8436-7

Key words

Search

Navigation