Skip to main content
SpringerLink
Log in

Survival Analysis of Stochastic Competitive Models in a Polluted Environment and Stochastic Competitive Exclusion Principle

  • Original Article
  • Published:
Bulletin of Mathematical Biology Aims and scope Submit manuscript

Abstract

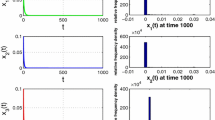
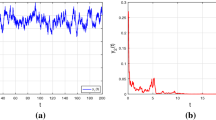
Stochastic competitive models with pollution and without pollution are proposed and studied. For the first system with pollution, sufficient criteria for extinction, nonpersistence in the mean, weak persistence in the mean, strong persistence in the mean, and stochastic permanence are established. The threshold between weak persistence in the mean and extinction for each population is obtained. It is found that stochastic disturbance is favorable for the survival of one species and is unfavorable for the survival of the other species. For the second system with pollution, sufficient conditions for extinction and weak persistence are obtained. For the model without pollution, a partial stochastic competitive exclusion principle is derived.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  • Alonso, D., Pascual, M., & McKane, J. A. (2007). Stochastic Amplification in Epidemics. J. R. Soc. Interface, 4, 575–582.

    Article  Google Scholar 

  • Arnold, L. (1974). Stochastic differential equations: theory and applications. Wiley: New York.

    MATH  Google Scholar 

  • Bahar, A., & Mao, X. (2004). Stochastic delay Lotka–Volterra model. J. Math. Anal. Appl., 292, 364–380.

    Article  MathSciNet  MATH  Google Scholar 

  • Bandyopadhyay, M., & Chattopadhyay, J. (2005). Ratio-dependent predator-prey model: effect of environmental fluctuation and stability. Nonlinearity, 18, 913–936.

    Article  MathSciNet  MATH  Google Scholar 

  • Beddington, J. R., & May, R. M. (1977). Harvesting natural populations in a randomly fluctuating environment. Science, 197, 463–465.

    Article  Google Scholar 

  • Braumann, C. A. (2002). Variable effort harvesting models in random environments: generalization to density-dependent noise intensities. Math. Biosci., 177& 178, 229–245.

    Article  MathSciNet  Google Scholar 

  • Braumann, C. A. (2007). Itô versus Stratonovich calculus in random population growth. Math. Biosci., 206, 81–107.

    Article  MathSciNet  MATH  Google Scholar 

  • Braumann, C. A. (2008). Growth and extinction of populations in randomly varying environments. Comput. Math. Appl., 56, 631–644.

    Article  MathSciNet  MATH  Google Scholar 

  • Cattiaux, P. Méléard, S. (2009). Competitive or weak cooperative stochastic Lotka–Volterra systems conditioned on non-extinction. J. Math. Biol., doi: 10.1007/s00285-009-0285-4.

    Google Scholar 

  • Chattopadhyay, J. (1996). Effect of toxic substances on a two species competitive system. Ecol. Model., 84, 287–289.

    Article  Google Scholar 

  • Du, N. H., & Sam, V. H. (2006). Dynamics of a stochastic Lotka–Volterra model perturbed by white noise. J. Math. Anal. Appl., 324, 82–97.

    Article  MathSciNet  MATH  Google Scholar 

  • Freedman, H. I., & Shukla, J. B. (1991). Models for the effect of toxicant in single-species and predator-prey systems. J. Math. Biol., 30, 15–30.

    Article  MathSciNet  MATH  Google Scholar 

  • Gard, T. C. (1984). Persistence in stochastic food web models. Bull. Math. Biol., 46, 357–370.

    MathSciNet  MATH  Google Scholar 

  • Gard, T. C. (1986). Stability for multispecies population models in random environments. Nonlinear Anal., 10, 1411–1419.

    Article  MathSciNet  MATH  Google Scholar 

  • Gard, T. C. (1988). Introductions to stochastic differential equations. New York.

  • Gard, T. C. (1992). Stochastic models for toxicant-stressed populations. Bull. Math. Biol., 54, 827–837.

    MATH  Google Scholar 

  • Gillespiea, D. T. (2000). The chemical Langevin equation. J. Chem. Phys., 113, 297–306.

    Article  Google Scholar 

  • Hallam, T. G., Clark, C. E., & Lassider, R. R. (1983a). Effects of toxicant on population: a qualitative approach I. Equilibrium environmental exposure. Ecol. Model., 8, 291–304.

    Article  Google Scholar 

  • Hallam, T. G., Clark, C. E., & Jordan, G. S. (1983b). Effects of toxicant on population: a qualitative approach II. First Order Kinetics. J. Math. Biol., 18, 25–37.

    Article  MATH  Google Scholar 

  • Hallam, T. G., & Deluna, J. L. (1984). Effects of toxicant on populations: a qualitative approach III. Environmental and food chain pathways. J. Theor. Biol., 109, 411–429.

    Article  Google Scholar 

  • Hallam, T. G., & Ma, Z. (1986). Persistence in population models with demographic fluctuations. J. Math. Biol., 24, 327–339.

    Article  MathSciNet  MATH  Google Scholar 

  • Hallam, T. G., & Ma, Z. (1987). On density and extinction in continuous population model. J. Math. Biol., 25, 191–201.

    Article  MathSciNet  MATH  Google Scholar 

  • Hardin, G. (1960). The competitive exclusion principle. Science, 131, 1292–1297.

    Article  Google Scholar 

  • He, J., & Wang, K. (2007). The survival analysis for a single-species population model in a polluted environment. Appl. Math. Model., 31, 2227–2238.

    Article  MATH  Google Scholar 

  • He, J., & Wang, K. (2009). The survival analysis for a population in a polluted environment. Nonlinear Anal. Real World Appl., 10, 1555–1571.

    Article  MathSciNet  MATH  Google Scholar 

  • Higham, D. J. (2001). An algorithmic introduction to numerical simulation of stochastic differential equations. SIAM Rev., 43, 525–546.

    Article  MathSciNet  MATH  Google Scholar 

  • Hsu, S. B., Luo, T. K., & Waltman, P. (1995). Competition between plasmid-bearing and plasmid-free organisms in a chemostat with an inhibitorm. J. Math. Biol., 34, 225–238.

    Article  MathSciNet  MATH  Google Scholar 

  • Ikeda, N., & Watanabe, S. (1977). A comparison theorem for solutions of stochastic differential equations and its applications. Osaka J. Math. 619–633.

  • Jensen, A. L., & Marshall, J. S. (1982). Application of a surplus production model to assess environmental impacts on exploited populations of Daphnia pluex in the laboratory. Environ. Pollut., 28, 273–280.

    Article  Google Scholar 

  • Li, X., & Mao, X. (2009). Population dynamical behavior of non-autonomous Lotka–Volterra competitive system with random perturbation. Discrete Contin. Dyn. Syst., 24, 523–545.

    Article  MathSciNet  MATH  Google Scholar 

  • Liu, H., & Ma, Z. (1991). The threshold of survival for system of two species in a polluted environment. J. Math. Biol., 30, 49–51.

    Article  MathSciNet  MATH  Google Scholar 

  • Liu, M., & Wang, K. (2009). Survival analysis of stochastic single-species population models in polluted environments. Ecol. Model., 220, 1347–1357.

    Article  Google Scholar 

  • Liu, M., & Wang, K. (2010). Persistence and extinction of a stochastic single-specie model under regime switching in a polluted environment. J. Theor. Biol., 264, 934–944.

    Article  Google Scholar 

  • Ludwig, D. (1975). Persistence of dynamical systems under random perturbations. SIAM. Rev., 17, 605–640.

    Article  MathSciNet  MATH  Google Scholar 

  • Luna, J. T., & Hallam, T. G. (1987). Effects of toxicants on population: a qualitative approach IV. Resources-consumer-toxicant models. Ecol. Model., 35, 249–273.

    Article  Google Scholar 

  • Luo, Q., & Mao, X. (2007). Stochastic population dynamics under regime switching. J. Math. Anal. Appl., 334, 69–84.

    Article  MathSciNet  MATH  Google Scholar 

  • Ma, Z., Song, B., & Hallam, T. G. (1989). The threshold of survival for systems in a fluctuating environment. Bull. Math. Biol., 51, 311–323.

    MATH  Google Scholar 

  • Mao, X., Marion, G., & Renshaw, E. (2002). Environmental Brownian noise suppresses explosions in populations dynamics. Stoch. Process. Appl., 97, 95–110.

    Article  MathSciNet  MATH  Google Scholar 

  • Mao, X., Sabanis, S., & Renshaw, E. (2003). Asymptotic behaviour of the stochastic Lotka–Volterra model. J. Math. Anal. Appl., 287, 141–156.

    Article  MathSciNet  MATH  Google Scholar 

  • Mao, X. (2005). Delay population dynamics and environmental noise. Stoch. Dyn., 5, 149–162.

    Article  MathSciNet  MATH  Google Scholar 

  • Mao, X., & Yuan, C. (2006). Stochastic differential equations with Markovian switching. London: Imperial College Press.

    MATH  Google Scholar 

  • May, R. M. (2001). Stability and complexity in model ecosystems. Princeton University Press: Princeton.

    MATH  Google Scholar 

  • McKane, A. J., & Newman, T. J. (2005). Predator-prey cycles from resonant amplification of demographic stochasticity. Phys. Rev. Lett., 94, 218102.

    Article  Google Scholar 

  • Nelson, S. A. (1970). The problem of oil pollution of the sea. In Advances in marine biology (pp. 215–306). London: Academic Press.

    Google Scholar 

  • Øsendal, B. (1998). Stochastic differential equations: an introduction with applications (5th ed.). Berlin: Springer.

    Google Scholar 

  • Pang, S., Deng, F., & Mao, X. (2008). Asymptotic properties of stochastic population dynamics, Dynamics of Continuous. Dyn. Contin. Discrete Impuls. Syst. Ser. A Math. Anal., 15, 603–620.

    MathSciNet  MATH  Google Scholar 

  • Rudnicki, R., & Pichor, K. (2007). Influence of stochastic perturbation on prey-predator systems. Math. Biosci., 206, 108–119.

    Article  MathSciNet  MATH  Google Scholar 

  • Samanta, G. P., & Maiti, A. (2004). Dynamical model of a single-species system in a polluted environment. J. Appl. Math. Comput., 16, 231–242.

    Article  MathSciNet  MATH  Google Scholar 

  • Shukla, J. B., & Dubey, B. (1996). Simultaneous effect of two toxicants on biological species: a mathematical model. J. Biol. Syst., 4, 109–130.

    Article  Google Scholar 

  • Shukla, J. B., Freedman, H. I., Pal, V. N., Misra, O. P., Agarwal, M., & Shukla, A. (1989). Degradation and subsequent regeneration of a forestry resource: a mathematical model. Ecol. Model., 44, 219–229.

    Article  Google Scholar 

  • Thomas, D. M., Snell, T. W., & Joffer, S. M. (1996). A control problem in a polluted environment. Math. Biosci., 133, 139–163.

    Article  MATH  Google Scholar 

  • Turelli, M. (1977). Random environments and stochastic calculus. Theor. Pop. Biol., 12, 140–178.

    Article  MathSciNet  MATH  Google Scholar 

  • Zhu, C., & Yin, G. (2009). On competitive Lotka–Volterra model in random environments. J. Math. Anal. Appl., 357, 154–170.

    Article  MathSciNet  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mathematics, Harbin Institute of Technology, Weihai, 264209, P.R. China

    Meng Liu, Ke Wang & Qiong Wu

  2. School of Mathematics and Statistics, Northeast Normal University, Changchun, 130024, P.R. China

    Ke Wang

Authors
  1. Meng Liu
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Ke Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Qiong Wu
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Meng Liu.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Liu, M., Wang, K. & Wu, Q. Survival Analysis of Stochastic Competitive Models in a Polluted Environment and Stochastic Competitive Exclusion Principle. Bull Math Biol 73, 1969–2012 (2011). https://doi.org/10.1007/s11538-010-9569-5

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11538-010-9569-5

Keywords

Search

Navigation