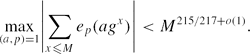Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Garaev, Moubariz Z.
and
Shen, Chun-Yen
2010.
On the size of the set A(A + 1).
Mathematische Zeitschrift,
Vol. 265,
Issue. 1,
p.
125.
Гараев, Мубарис Зафар оглы
and
Garaev, Mubaris Zafar ogly
2010.
Суммы и произведения множеств и оценки рациональных тригонометрических сумм в полях простого порядка.
Успехи математических наук,
Vol. 65,
Issue. 4,
p.
5.
Bourgain, Jean
2010.
Additive Number Theory.
p.
9.
Shparlinski, Igor E.
2010.
On the size of the Gelfond exponent.
Journal of Number Theory,
Vol. 130,
Issue. 4,
p.
1056.
GUTIERREZ, JAIME
and
SHPARLINSKI, IGOR E.
2010.
EXPANSION OF ORBITS OF SOME DYNAMICAL SYSTEMS OVER FINITE FIELDS.
Bulletin of the Australian Mathematical Society,
Vol. 82,
Issue. 2,
p.
232.
SHPARLINSKI, IGOR E.
2010.
ON POINT SETS IN VECTOR SPACES OVER FINITE FIELDS THAT DETERMINE ONLY ACUTE ANGLE TRIANGLES.
Bulletin of the Australian Mathematical Society,
Vol. 81,
Issue. 1,
p.
114.
Ostafe, Alina
and
Shparlinski, Igor E.
2010.
Pseudorandom numbers and hash functions from iterations of multivariate polynomials.
Cryptography and Communications,
Vol. 2,
Issue. 1,
p.
49.
Murty, M. Ram
2010.
Small solutions of polynomial congruences.
Indian Journal of Pure and Applied Mathematics,
Vol. 41,
Issue. 1,
p.
15.
Helfgott, Harald Andrés
and
Rudnev, Misha
2011.
AN EXPLICIT INCIDENCE THEOREM IN.
Mathematika,
Vol. 57,
Issue. 1,
p.
135.
Li, Liangpan
and
Roche-Newton, Oliver
2011.
An improved sum-product estimate for general finite fields.
SIAM Journal on Discrete Mathematics,
Vol. 25,
Issue. 3,
p.
1285.
Bourgain, J.
and
Glibichuk, A.
2011.
Exponential sum estimates over a subgroup in an arbitrary finite field.
Journal d'Analyse Mathématique,
Vol. 115,
Issue. 1,
p.
51.
Bourgain, J.
Konyagin, S. V.
and
Shparlinski, I. E.
2011.
Distribution of Elements of Cosets of Small Subgroups and Applications.
International Mathematics Research Notices,
Cilleruelo, Javier
and
Garaev, Moubariz Z.
2011.
Concentration of Points on Two and Three Dimensional Modular Hyperbolas and Applications.
Geometric and Functional Analysis,
Vol. 21,
Issue. 4,
p.
892.
Bourgain, Jean
Dilworth, Stephen
Ford, Kevin
Konyagin, Sergei
and
Kutzarova, Denka
2011.
Explicit constructions of RIP matrices and related problems.
Duke Mathematical Journal,
Vol. 159,
Issue. 1,
Bourgain, Jean
Dilworth, Stephen J.
Ford, Kevin
Konyagin, Sergei V.
and
Kutzarova, Denka
2011.
Breaking the k
2
barrier for explicit RIP matrices
.
p.
637.
Hart, Derrick
Li, Liangpan
and
Shen, Chun-Yen
2012.
Fourier analysis and expanding phenomena in finite fields.
Proceedings of the American Mathematical Society,
Vol. 141,
Issue. 2,
p.
461.
Kaczorowski, J.
and
Molteni, G.
2012.
Extremal values for the sum ∑r=1τe(a2r/q).
Journal of Number Theory,
Vol. 132,
Issue. 11,
p.
2595.
SHPARLINSKI, IGOR
2012.
SUM–PRODUCT ESTIMATES AND MULTIPLICATIVE ORDERS OFγANDγ+γ−1IN FINITE FIELDS.
Bulletin of the Australian Mathematical Society,
Vol. 85,
Issue. 3,
p.
505.
Hegyvári, Norbert
2012.
Some remarks on multilinear exponential sums with an application.
Journal of Number Theory,
Vol. 132,
Issue. 1,
p.
94.
Rudnev, Misha
2012.
An Improved Sum–Product Inequality in Fields of Prime Order.
International Mathematics Research Notices,
Vol. 2012,
Issue. 16,
p.
3693.
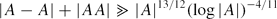 for any subset A ⊂ Fp with 1 < |A| < p12/23. Then we apply our estimate to obtain explicit bounds for some exponential sums in Fp. We show that for any subsets X, Y, Z ⊂ F*p and any complex numbers αx, βy, γz with |αx| ≤ 1, |βy| ≤ 1, |γz| ≤ 1, the following bound holds:
for any subset A ⊂ Fp with 1 < |A| < p12/23. Then we apply our estimate to obtain explicit bounds for some exponential sums in Fp. We show that for any subsets X, Y, Z ⊂ F*p and any complex numbers αx, βy, γz with |αx| ≤ 1, |βy| ≤ 1, |γz| ≤ 1, the following bound holds:
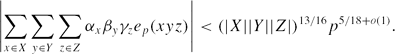 We apply this bound further to show that if H is a subgroup of F*p with |H| > p1/4, then
We apply this bound further to show that if H is a subgroup of F*p with |H| > p1/4, then
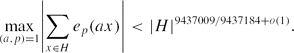 Finally we show that if g is a generator of F*p then for any M < p the number of solutions of the equation
Finally we show that if g is a generator of F*p then for any M < p the number of solutions of the equation
 is less than
is less than 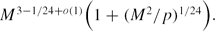 . This implies that if p1/2 < M < p, then
. This implies that if p1/2 < M < p, then