Hostname: page-component-76fb5796d-45l2p Total loading time: 0 Render date: 2024-04-25T07:31:00.173Z Has data issue: false hasContentIssue false
  • English
  • Français

12.—Spectral Theory of Rotating Chains

Published online by Cambridge University Press:  14 February 2012

C. A. Stuart
C. A. Stuart
Affiliation:
Battelle Institute, 7 Route de Drize, Carouge, Geneva
Get access Rights & Permissions [Opens in a new window]

Synopsis

Two eigenvalue problems associated with steady rotations of a chain are considered. To compare the spectra of these two problems, let σK(n) denote the set of all angular velocities with which a chain of unit length with one end fixed and the other free can rotate in a vertical plane so as to have exactly n nodes on thevertical axis (including the fixed end). In a linearised theory σK(n) is a single point, i.e.

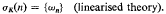
In the full non-linear theory σK(n) is an infinite interval lying to the right of ⍵n. Indeed,

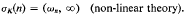
This is established in [1].

Next, let σM(β, n) denote the set of all angular velocities with which a chain, having ends fixed at unit distance apart on the vertical axis, can rotate in a vertical plane so as to have exactly n+l nodes on the vertical axis (including the ends) and so that the tension takes the value β at the lower end. This problem, in which the length of the chain is not prescribed is a model for a spinning process in which the ‘chain’ is continuously created in a rotating configuration. For β>0, we again have in the linearised theory that σM(β, n) is a singleton, i.e.

In the full non-linear theory σM(β, n) lies to the left of λn(β). Although unable to determine exactly σM(β, n) for β>0, we have

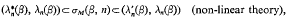
where ⍵n λn(β), 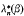and 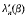are all characterised as the nth zeros of known combinations of Bessel functions.

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 73 , 1975 , pp. 199 - 214
Copyright
Copyright © Royal Society of Edinburgh 1975

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Kolodner, I. I., Heavy rotating string—a non-linear eigenvalue problem. Comm. Pure Appl. Math., 8, 395–408, 1955.Google Scholar
2Crandall, M. G. and Rabinowitz, P. H., Non-linear Sturm-Liouville eigenvalue problems and topological degree. J. Math. Mech., 19, 1083–1102, 1970.Google Scholar
3Rabinowitz, P. H., Non-linear Sturm-Liouville eigenvalue problems for second order differential equations. Comm. Pure Appl. Math., 23, 939–961, 1970.CrossRefGoogle Scholar
4Rabinowitz, P. H., Some global results for non-linear eigenvalue problems. J.Functional Analysis, 8, 487–513, 1971.CrossRefGoogle Scholar
5Rabinowitz, P. H., Some aspects of non-linear eigenvalue problems. Rocky Mountain J. Math.,23, 1973.Google Scholar
6Turner, R. E. L., Non-linear eigenvalue problems with non-local operators. Comm. Pure Appl. Math., 23, 963–972, 1970.CrossRefGoogle Scholar
7Turner, R. E. L., Transversality in non-linear eigenvalue problems. In Non-linear Functional Analysis (Ed. Zarantonello, E. H.). New York: Academic Press, 1971.Google Scholar
8Stuart, C. A., Some bifurcation theory for k-set contractions. Proc. London Math. Soc, 27, 531–550, 1973.Google Scholar
9Stuart, C. A., Global properties of components of solutions of non-linear second order ordinary differential equations on the half-line. Battelle Math. Rep., 75: Ann. Scuola Norm. Sup. Pisa (to appear).Google Scholar
10Krasnoselskii, M. A., Topological Methods in the Theory of Non-linear Integral Equations. London: Pergamon, 1964.Google Scholar
11Jahnke, E. and Emde, F., Tables of Functions (4th edn.). New York: Dover, 1945.Google Scholar
12Courant, R. and Hilbert, D., Methods of Mathematical Physics, I. New York: Interscience, 1953.Google Scholar
13Stuart, C. A., Spectral theory of rotating chains. Battelle Math. Rep., 84, 1974.Google Scholar