Hostname: page-component-8448b6f56d-m8qmq Total loading time: 0 Render date: 2024-04-24T15:53:50.925Z Has data issue: false hasContentIssue false
  • English
  • Français

Restrictions on microstructure

Published online by Cambridge University Press:  14 November 2011

Kaushik Bhattacharya ,
Nikan B. Firoozye ,
Richard D. James  and
Robert V. Kohn
Kaushik Bhattacharya
Affiliation:
Div. of Engrng, Caltech, Pasadena, CA 91125, U.S.A.
Nikan B. Firoozye
Affiliation:
Dept. of Mathematics, Univ. of Illinois, Urbana, IL 61801, U.S.A.
Richard D. James
Affiliation:
Aero. Engrng and Mechanics, University of Minnesota, Minneapolis, MN 55455, U.S.A.
Robert V. Kohn
Affiliation:
Courant Institute, 251 Mercer Street, New York, NY 10012, U.S.A.
Get access Rights & Permissions [Opens in a new window]

Extract

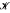We consider the following question: given a set of matrices with no rank-one connections, does it support a nontrivial Young measure limit of gradients? Our main results are these: (a) a Young measure can be supported on four incompatible matrices; (b) in two space dimensions, a Young measure cannot be supported on finitely many incompatible elastic wells; (c) in three or more space dimensions, a Young measure can be supported on three incompatible elastic wells; and (d) if 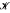supports a nontrivial Young measure with mean value 0, then the linear span of 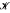must contain a matrix of rank one.

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 124 , Issue 5 , 1994 , pp. 843 - 878
Copyright
Copyright © Royal Society of Edinburgh 1994

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Adams, J. F.. On the non-existence of elements of Hopf invariant one. Ann. Math. 72 (1960), 20–104.CrossRefGoogle Scholar
2Adams, J. F. and Atiyah, M. F.. K-theory and the Hopf invariant. Quart. J. Math. Oxford (2) 17 (1966), 31–38.CrossRefGoogle Scholar
3Adem, J.. On nonsingular bilinear maps. In The Steenrod Algebra and its Applications, ed. Peterson, F. P., Lecture Notes in Mathematics 168, 11–24 (Berlin: Springer, 1970).Google Scholar
4Adem, J.. On nonsingular bilinear maps II. Bol. Soc. Mat. Mexicana 16 (1971), 64–70.Google Scholar
5Allaire, G. and Kohn, R. V.. Optimal lower bounds on the elastic energy of a composite made from two non well-ordered isotropic materials. Quart. Appl. Math, (to appear).Google Scholar
6Ball, J.M.. On the paper ‘Basic calculus of variations’. Pacific J. Math. 116 (1985), 7–10.CrossRefGoogle Scholar
7Ball, J. M.. A version of the fundamental theorem for Young measures. In Lecture Notes in Physics 344, eds. Rascle, M. et al. , 207–215 (Berlin: Springer, 1989).Google Scholar
8Ball, J. M.. Sets of gradients with no rank-one connections. J. Math. Pures Appl. 69 (1990), 241–259.Google Scholar
9Ball, J. M. and James, R. D.. Fine phase mixtures as minimizers of energy. Arch. Rational Mech. Anal. 100(1987), 13–52.CrossRefGoogle Scholar
10Ball, J. M. and James, R. D.. Proposed experimental tests of a theory of fine microstructure and the two-well problem. Philos. Trans. R. Soc. London Ser. A 338 (1992), 389–450.CrossRefGoogle Scholar
11Bhattacharya, K.. Wedge-like microstructure in martensite. Ada Metall. Mater. 39 (1991), 2431–2444.CrossRefGoogle Scholar
12Bhattacharya, K.. Comparison of the geometrically nonlinear and linear theories of martensitic transformation. Contin. Mech. Thermodyn. 5 (1993), 205–243.CrossRefGoogle Scholar
13Chipot, M. and Kinderlehrer, D.. Equilibrium configurations of crystals. Arch. Rational Mech. Anal. 103 (1988), 237–277.CrossRefGoogle Scholar
14Dacorogna, B.. Direct Methods in the Calculus of Variations (Berlin: Springer, 1989).CrossRefGoogle Scholar
15DiPerna, R. J.. Compensated compactness and general systems of conservation laws. Trans. Amer. Math. Soc. 292 (1985), 383–420.CrossRefGoogle Scholar
16Firoozye, N. B.. Optimal use of the translation method and relaxation of variational problems. Comm. Pure Appl. Math. 44 (1991), 643–678.CrossRefGoogle Scholar
17Firoozye, N. B. and Kohn, R. V. et al. . Geometric parameters and the relaxation of multiwell energies. In Microstructure and Phase Transition, eds. Kinderlehrer, D., 85–110 (Berlin: Springer, 1993).CrossRefGoogle Scholar
18Francfort, G. A. and Milton, G. W.. Sets of conductivity and elasticity tensors stable under lamination. Comm. Pure Appl. Math, (to appear).Google Scholar
19Hombogen, E.. The fractal nature of martensite/austenite microstructures. Materials Sci. Forum 56–58 (1990), 131–138.CrossRefGoogle Scholar
20James, R. D. and Kinderlehrer, D.. Theory of diffusionless phase transformations. In Lecture Notes in Physics 344, eds. Rascle, M. et al. , 51–84 (Berlin: Springer, 1989).Google Scholar
21Jodeit, M. and Olver, P. J.. On the equation grad f = M grad g. Proc. Roy. Soc. Edinburgh Sect. A 116 (1990), 341–358.CrossRefGoogle Scholar
22John, F.. Bounds for deformations in terms of average strains. In Inequalities III, ed. Shisha, O., 129–144 (New York: Academic Press, 1972).Google Scholar
23Khachaturyan, A. G.. Theory of Structural Transformations in Solids (Chichester: John Wiley, 1983).Google Scholar
24Kinderlehrer, D.. Remarks about equilibrium configurations of crystals. In Material Instabilities in Continuum Mechanics, ed. Ball, J. M., 217–241 (Oxford: Oxford University Press, 1988).Google Scholar
25Kinderlehrer, D. and Pedregal, P.. Characterizations of gradient Young measures. Arch. Rational Mech. Anal. 115 (1991), 329–365.CrossRefGoogle Scholar
26Kohn, R. V.. The relaxation of a double-well energy. Contin. Mech. Thermodyn. 3 (1991), 981–1000.CrossRefGoogle Scholar
27Kohn, R. V. and Muller, S.. Surface energy and microstructure in coherent phase transitions. Comm. Pure Appl. Math, (to appear).Google Scholar
28Kohn, R. V. and Strang, G.. Optimal design and relaxation of variational problems I, II, III. Comm. Pure Appl. Math. 39 (1986) 113–137; 139–182; 353–377.CrossRefGoogle Scholar
29Lam, K. Y.. Construction of nonsingular bilinear maps. Topology 6 (1967), 423–426.CrossRefGoogle Scholar
30Lam, K. Y.. Some interesting examples of nonsingular bilinear maps. Topology 16 (1977), 185–188.CrossRefGoogle Scholar
31Matos, J. P.. Young measures and the absence of fine microstructures in a class of phase transitions. European J. Appl. Math. 3 (1992), 31–54.CrossRefGoogle Scholar
32Milton, G. W.. On characterizing the set of possible effective tensors of composites: the variational method and the translation method. Comm. Pure Appl. Math. 42 (1990), 63–125.CrossRefGoogle Scholar
33Milton, G. W.. A link between sets of tensors stable under lamination and quasiconvexity. Comm. Pure Appl. Math, (to appear).Google Scholar
34Milton, G. W. and Nesi, V.. Polycrystalline configurations that maximize electrical resistivity. J. Mech. Phys. Solids 39 (1991), 525–542.Google Scholar
35Murat, F.. A survey on compensated compactness. In Contributions to the Modern Calculus of Variations, ed. Cesari, L., 145–183 (London: Pitman, 1987).Google Scholar
36Pedregal, P.. The concept of a laminate. In Microstructure and Phase Transition, eds. Kinderlehrer, D. et al. , 129–142 (Berlin: Springer, 1993).CrossRefGoogle Scholar
37Pedregal, P.. Laminates and microstructure. European J. Appl. Math. 4 (1993), 121–149.CrossRefGoogle Scholar
38Reshetnyak, Yu. G.. Liouville's theorem on conformal mappings with minimal regularity assumptions. Siberian Math. J. 8 (1967), 631–653.CrossRefGoogle Scholar
39Roitburd, A. L.. Martensitic transformation as a typical phase transformation in solids. Solid State Physics 33 (1978), 317–390.CrossRefGoogle Scholar
40Serre, D.. Formes quadratiques et calcul des variations. J. Math. Pures Appl. 62 (1983), 177–196.Google Scholar
41Šverak, V.. On the problem of two wells. In Microstructure and Phase Transition, eds. Kinderlehrer, D. et al. , 183–190 (Berlin: Springer, 1993).CrossRefGoogle Scholar
42Šverák, V.. Rank-one convexity does not imply quasiconvexity. Proc. Roy. Soc. Edinburgh Sect. A 120(1992), 185–189.CrossRefGoogle Scholar
43Šverák, V.. New examples of quasiconvex functions. Arch. Rational Mech. Anal. 119 (1992), 293–300.CrossRefGoogle Scholar
44Šverák, V.. On Tartar's conjecture. Ann. Inst. H. Poincaré, Anal. Non Linéaire 10 (1993), 405–412.CrossRefGoogle Scholar
45Šverák, V.. On regularity for the Monge-Ampère equation (preprint).Google Scholar
46Tartar, L.. Compensated compactness and applications to partial differential equations. In Nonlinear Analysis and Mechanics, ed. Knops, R., Pitman Research Notes in Mathematics 39, 136–212 (London: Pitman, 1978).Google Scholar
47Tartar, L.. The compensated compactness method applied to systems of conservation laws. In Systems of Nonlinear Partial Differential Equations, ed. Ball, J. M., 263–285 (Dordrecht: D. Reidel, 1983).CrossRefGoogle Scholar
48Tartar, L.. Some remarks on separately convex functions. In Microstructure and Phase Transition, eds. Kinderlehrer, D. et al. , 191–204 (Berlin: Springer, 1993).CrossRefGoogle Scholar
49Terpstra, F. J.. Die darstellung biquadratischer formen als summen von quadraten mit anwendung auf die variationsrechnung. Math. Ann. 116(1938), 166–180.CrossRefGoogle Scholar
50Zhang, K.. A construction of quasiconvex functions with linear growth at infinity. Ann. Scuola Normale Pisa Ser. IV 19 (1992) 313–326.Google Scholar
51Zhang, K.. Rank-one connections and the three well problem. Trans. A.M.S. (to appear).Google Scholar