Abstract
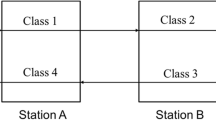
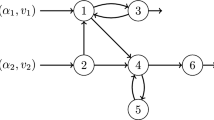
We consider a stochastic queueing network with fixed routes and class priorities. The vector of class sizes forms a homogeneous Markov process of countable state space Z6 +. The network is said “stable” (resp.“unstable”) if this Markov process is ergodic (resp. transient). The parameters are the traffic intensities of the different classes. An unusual condition of stability is obtained thanks to a new argument based on the characterization of the “essential states”. The exact stability conditions are then detected thanks to an associated fluid network: we identify a zone of the parameter space in which diverging, fluid paths appear. In order to show that this is a zone of instability (and that the network is stable outside this zone), we resort to the criteria of ergodicity and transience proved by Malyshev and Menshikov for reflected random walks in Z6 + (Malyshev and Menshikov, 1981). Their approach allows us to neglect some “pathological” fluid paths that perturb the dynamics of the fluid model. The stability conditions thus determined have especially unusual characteristics: they have a quadratic part, the stability domain is not convex, and increasing all the service rates may provoke instability (Theorem 1.1 and section 7).
Similar content being viewed by others
References
D. Bertsimas, D. Gamarnik and J. Tsitsiklis, Stability conditions for multiclass fluid queueing networks, Working paper OR 303–95, Massachusetts Institute of Technology, Cambridge (January, 1995).
D. Botvitch and A. Zamyatin, Ergodicity of conservative communication networks, Rapport de recherche 1772, INRIA (October, 1992).
M. Bramson, Instability of FIFO queueing networks, Annals of Applied Probability 4 (1994) 414–431.
M. Bramson, Convergence to equilibria for fluid models of FIFO queueing networks, Queueing Systems 22 (1996) 5–45.
H. Chen and A. Mandelbaum, Discrete flow networks: bottleneck analysis and fluid approximations, Mathematics of Operations Research 16 (1991) 408–446.
R. Cruz, A calculus for network delay, Part II: Network analysis, IEEE Transactions on Information Theory 37(1) (January, 1991) 132–141.
J. Dai, On positive Harris recurrence of multiclass queueing networks: a unified approach via fluid limit models, Annals of Applied Probability 5(1) (1993) 49–77.
J. Dai, Instability of multiclass queueing networks, Preprint (June, 1995).
J. Dai and G. Weiss, Stability and instability of fluid models for re-entrant lines, to appear in Mathematics of Operations Research.
J.G. Dai and J.H.V. Vate, Virtual stations and the capacity of two-station queueing networks, Preprint (March, 1996).
V. Dumas, Essential faces and stability conditions of multiclass networks with priorities, submitted to Markov Processes and Related Fields.
V. Dumas, Approches fluides pour la stabilité et l'instabilité de réseaux de files d'attente stochastiques à plusieurs classes de clients, Thèse de Doctorat de l'École Polytechnique, École Polytechnique (Décembre, 1995).
V. Dumas, Instability cycles in fluid Bramson networks, submitted to IEEE Transactions on Automatic Control.
W. Feller, An Introduction to Probability Theory and Its Applications, volume I, chapter XV: Markov Chains (Wiley, New York, 1968).
S. Foss and A. Rybko, Stability of multiclass Jackson-type networks, submitted to Advances in Applied Probability.
J. Harrison and V. Nguyen, Brownian models of multiclass queueing networks: current status and open problems, Queueing Systems 13 (1993) 5–40.
C. Humes, Jr., A regulator stabilization technique: Kumar-Seidman revisited, IEEE Transactions on Automatic Control 39(1) (January, 1994) 191–196.
F. Kelly, Reversibility and Stochastic Networks (Wiley, New York, 1979).
P. Kumar and T. Seidman, Dynamic instabilities and stabilization methods in distributed real-time scheduling of manufacturing systems, IEEE Transactions on Automatic Control 35(3) (March, 1990) 289–298.
S. Lu and P. Kumar, Distributed scheduling based on due dates and buffer priorities, IEEE Transactions on Automatic Control 36(12) (December, 1991) 1406–1416.
V. Malyshev, Networks and dynamical systems, Advances in Applied Probability 25 (1993) 140–175.
V. Malyshev and M. Menshikov, Ergodicity, continuity, and analyticity of countable Markov chains, Transactions of the Moscow Mathematical Society 1 (1981) 1–47.
S. Meyn, Transience of multiclass queueing networks via fluid limit models, Annals of Applied Probability 5(4) (November, 1995) 946–957.
A. Rybko and A. Stolyar, Ergodicity of stochastic processes describing the operation of open queueing networks, Problemy Peredachi Informatsii 28(3) (July-September, 1992) 3–26.
Rights and permissions
About this article
Cite this article
Dumas, V. A multiclass network with non-linear, non-convex, non-monotonic stability conditions. Queueing Systems 25, 1–43 (1997). https://doi.org/10.1023/A:1019122115228
Issue Date:
DOI: https://doi.org/10.1023/A:1019122115228