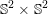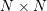Among compact, simply connected, even-dimensional smooth manifolds, the examples known to admit a Riemannian metric with positive sectional curvature form a short list: spheres, complex projective spaces, quaternionic projective spaces, the Cayley plane, the three flag manifolds discovered by Wallach [Reference WallachWal72], and the biquotient
![]() $\text{SU}(2)//T^{2}$
discovered by Eschenburg [Reference EschenburgEsc84].
$\text{SU}(2)//T^{2}$
discovered by Eschenburg [Reference EschenburgEsc84].
In order to find additional examples, it is natural to look among metrics with symmetry. This strategy has recently resulted in a new example in dimension seven (see Dearricott [Reference DearricottDea11] and Grove et al. [Reference Grove, Verdiani and ZillerGVZ11]). To narrow the search, one seeks topological obstructions to positive curvature and symmetry. This broad research program was formulated by Grove and developed by him and many others over the past two decades (see Grove [Reference GroveGro09], Wilking [Reference WilkingWil07], and Ziller [Reference ZillerZil07, Reference ZillerZil14] for surveys).
In this article, we prove further topological restrictions in the presence of torus symmetry. Our first theorem considers the case where the positively curved Riemannian manifold
![]() $M^{2n}$
(
$M^{2n}$
(
![]() $n>2$
) has vanishing fourth Betti number. To motivate this assumption, recall that, if the rank of the isometric torus action exceeds
$n>2$
) has vanishing fourth Betti number. To motivate this assumption, recall that, if the rank of the isometric torus action exceeds
![]() $\log _{4/3}(2n-3)$
, then the Betti numbers of
$\log _{4/3}(2n-3)$
, then the Betti numbers of
![]() $M$
satisfy
$M$
satisfy
![]() $b_{2}(M)\leqslant b_{4}(M)\leqslant 1$
(see § 4).
$b_{2}(M)\leqslant b_{4}(M)\leqslant 1$
(see § 4).
Theorem A. Let
![]() $M^{2n}$
$M^{2n}$
![]() $(n>2)$
be a simply connected, closed manifold with
$(n>2)$
be a simply connected, closed manifold with
![]() $b_{4}(M)=0$
. Assume
$b_{4}(M)=0$
. Assume
![]() $M$
admits a Riemannian metric with positive sectional curvature invariant under the action of a torus
$M$
admits a Riemannian metric with positive sectional curvature invariant under the action of a torus
![]() $T$
with
$T$
with
![]() $\dim (T)>\log _{4/3}(2n-3)$
. The following hold:
$\dim (T)>\log _{4/3}(2n-3)$
. The following hold:
-
(1) the Euler characteristic satisfies
 $\unicode[STIX]{x1D712}(M)=\unicode[STIX]{x1D712}(\mathbb{S}^{2n})=2$
;
$\unicode[STIX]{x1D712}(M)=\unicode[STIX]{x1D712}(\mathbb{S}^{2n})=2$
; -
(2) the signature satisfies
 $\unicode[STIX]{x1D70E}(M)=\unicode[STIX]{x1D70E}(\mathbb{S}^{2n})=0$
;
$\unicode[STIX]{x1D70E}(M)=\unicode[STIX]{x1D70E}(\mathbb{S}^{2n})=0$
; -
(3) the fixed-point set
 $M^{T}$
is an even-dimensional rational sphere;
$M^{T}$
is an even-dimensional rational sphere; -
(4) for
 $g\in T$
,
$g\in T$
,
 $M^{g}$
is non-empty, and the number of components is at most two, with equality only if
$M^{g}$
is non-empty, and the number of components is at most two, with equality only if
 $g$
is an involution.
$g$
is an involution.
As an application of this result, consider an arbitrary closed manifold
![]() $N^{n}$
with
$N^{n}$
with
![]() $n>2$
, and consider its two-fold product
$n>2$
, and consider its two-fold product
![]() $M^{2n}=N\times N$
. Suppose that
$M^{2n}=N\times N$
. Suppose that
![]() $M$
admits a metric with positive curvature and an isometric torus action of rank
$M$
admits a metric with positive curvature and an isometric torus action of rank
![]() $r>\log _{4/3}(2n-3)$
. By Synge’s theorem,
$r>\log _{4/3}(2n-3)$
. By Synge’s theorem,
![]() $M$
is simply connected. As mentioned above, it follows that
$M$
is simply connected. As mentioned above, it follows that
![]() $b_{2}(M)\leqslant b_{4}(M)\leqslant 1$
. By the Künneth formulas,
$b_{2}(M)\leqslant b_{4}(M)\leqslant 1$
. By the Künneth formulas,
![]() $b_{4}(M)=0$
. By Theorem A,
$b_{4}(M)=0$
. By Theorem A,
which is impossible. Hence
![]() $N\times N$
has no such metric. A similar conclusion can be drawn for connected sums. We summarize this corollary as follows.
$N\times N$
has no such metric. A similar conclusion can be drawn for connected sums. We summarize this corollary as follows.
Corollary B. Let
![]() $N^{n}$
be a closed manifold with
$N^{n}$
be a closed manifold with
![]() $n>2$
. The product
$n>2$
. The product
![]() $N\times N$
does not admit a Riemannian metric with positive sectional curvature and an isometric torus action of rank
$N\times N$
does not admit a Riemannian metric with positive sectional curvature and an isometric torus action of rank
![]() $r>\log _{4/3}(2n-3)$
. Similarly, if
$r>\log _{4/3}(2n-3)$
. Similarly, if
![]() $n$
is even and
$n$
is even and
![]() $\unicode[STIX]{x1D712}(N)\neq 2$
, the connected sum
$\unicode[STIX]{x1D712}(N)\neq 2$
, the connected sum
![]() $N\#N$
does not admit a positively curved metric invariant under a torus action of rank
$N\#N$
does not admit a positively curved metric invariant under a torus action of rank
![]() $r>\log _{4/3}(n-3)$
.
$r>\log _{4/3}(n-3)$
.
Hopf conjectured that
![]() $\mathbb{S}^{2}\times \mathbb{S}^{2}$
does not admit a Riemannian metric with positive sectional curvature. Corollary B can be seen as positive evidence for the generalized conjecture that no product
$\mathbb{S}^{2}\times \mathbb{S}^{2}$
does not admit a Riemannian metric with positive sectional curvature. Corollary B can be seen as positive evidence for the generalized conjecture that no product
![]() $N\times N$
admits such a metric.
$N\times N$
admits such a metric.
We also remark that Hsiang and Kleiner proved that
![]() $\mathbb{S}^{2}\times \mathbb{S}^{2}$
does not admit a Riemannian metric with positive sectional curvature and an isometric circle action (see [Reference Hsiang and KleinerHK89, Reference Grove and WilkingGW14]). Hence Corollary B also holds when
$\mathbb{S}^{2}\times \mathbb{S}^{2}$
does not admit a Riemannian metric with positive sectional curvature and an isometric circle action (see [Reference Hsiang and KleinerHK89, Reference Grove and WilkingGW14]). Hence Corollary B also holds when
![]() $n=2$
, and it can be seen as a partial generalization of the Hsiang–Kleiner result.
$n=2$
, and it can be seen as a partial generalization of the Hsiang–Kleiner result.
The conclusion of Theorem A can be improved by imposing additional topological conditions on
![]() $M$
. For example, suppose that
$M$
. For example, suppose that
![]() $M$
is rationally elliptic, as conjectured by Bott, Grove and Halperin (see [Reference GroveGro02, § 5]). Since
$M$
is rationally elliptic, as conjectured by Bott, Grove and Halperin (see [Reference GroveGro02, § 5]). Since
![]() $\unicode[STIX]{x1D712}(M)=2$
, it follows that the odd Betti numbers vanish, hence
$\unicode[STIX]{x1D712}(M)=2$
, it follows that the odd Betti numbers vanish, hence
![]() $M$
is a rational sphere. We summarize similar corollaries here (see § 3 for proofs).
$M$
is a rational sphere. We summarize similar corollaries here (see § 3 for proofs).
Corollary C. Let
![]() $M^{2n}$
be a simply connected, closed Riemannian manifold with
$M^{2n}$
be a simply connected, closed Riemannian manifold with
![]() $b_{4}(M)=0$
. Assume
$b_{4}(M)=0$
. Assume
![]() $M$
admits a metric with positive sectional curvature and an isometric torus action of rank greater than
$M$
admits a metric with positive sectional curvature and an isometric torus action of rank greater than
![]() $\log _{4/3}(2n-3)$
. The following hold:
$\log _{4/3}(2n-3)$
. The following hold:
-
(1) if
 $M$
has vanishing odd-dimensional rational cohomology, e.g., if
$M$
has vanishing odd-dimensional rational cohomology, e.g., if
 $M$
is rationally elliptic, then
$M$
is rationally elliptic, then
 $M$
is a rational
$M$
is a rational
 $\mathbb{S}^{2n}$
;
$\mathbb{S}^{2n}$
; -
(2) if
 $M$
is
$M$
is
 $p$
-elliptic for some prime
$p$
-elliptic for some prime
 $p\geqslant 2n$
, then
$p\geqslant 2n$
, then
 $M$
is a mod
$M$
is a mod
 $p$
homology
$p$
homology
 $\mathbb{S}^{2n}$
;
$\mathbb{S}^{2n}$
; -
(3) if
 $M$
has vanishing homology in odd degrees, then
$M$
has vanishing homology in odd degrees, then
 $M$
is homeomorphic to
$M$
is homeomorphic to
 $\mathbb{S}^{2n}$
;
$\mathbb{S}^{2n}$
; -
(4) if
 $M$
is a biquotient, then
$M$
is a biquotient, then
 $M$
is diffeomorphic to
$M$
is diffeomorphic to
 $\mathbb{S}^{2n}$
;
$\mathbb{S}^{2n}$
; -
(5) if
 $M$
admits a smooth, effective cohomogeneity-one action by a compact, connected Lie group, and if the homology of
$M$
admits a smooth, effective cohomogeneity-one action by a compact, connected Lie group, and if the homology of
 $M$
has no
$M$
has no
 $2$
-torsion, then
$2$
-torsion, then
 $M$
is equivariantly diffeomorphic to
$M$
is equivariantly diffeomorphic to
 $\mathbb{S}^{2n}$
equipped with a linear
$\mathbb{S}^{2n}$
equipped with a linear
 $G$
-action;
$G$
-action; -
(6) if
 $M$
is a symmetric space, then
$M$
is a symmetric space, then
 $M$
is isometric to
$M$
is isometric to
 $\mathbb{S}^{n}$
.
$\mathbb{S}^{n}$
.
We remark that the torus action in this corollary need not respect the biquotient, cohomogeneity-one, or symmetric space structure. We also remark that, whenever
![]() $M$
is spin and homeomorphic to
$M$
is spin and homeomorphic to
![]() $\mathbb{S}^{4k}$
, its elliptic genus vanishes. Corollary C can therefore be seen as further evidence for a conjecture by Dessai (see [Reference DessaiDes05, Reference DessaiDes07] and Weisskopf [Reference WeisskopfWei13]).
$\mathbb{S}^{4k}$
, its elliptic genus vanishes. Corollary C can therefore be seen as further evidence for a conjecture by Dessai (see [Reference DessaiDes05, Reference DessaiDes07] and Weisskopf [Reference WeisskopfWei13]).
Note that, in Corollary C,
![]() $M$
is a rational
$M$
is a rational
![]() $\mathbb{S}^{2n}$
if the torus action is equivariantly formal. Indeed, this assumption together with Theorem A implies that the odd Betti numbers of
$\mathbb{S}^{2n}$
if the torus action is equivariantly formal. Indeed, this assumption together with Theorem A implies that the odd Betti numbers of
![]() $M$
vanish (see § 3).
$M$
vanish (see § 3).
To prove Theorem A, we show that the fixed-point set
![]() $M^{T}$
of the torus action is a rational sphere. Since the Euler characteristic and signature of
$M^{T}$
of the torus action is a rational sphere. Since the Euler characteristic and signature of
![]() $M$
and
$M$
and
![]() $M^{T}$
agree, the first two conclusions immediately follow. In order to prove that
$M^{T}$
agree, the first two conclusions immediately follow. In order to prove that
![]() $M^{T}$
is a rational sphere, we combine two important ideas from previous work. The first involves proving the existence of fixed-point components
$M^{T}$
is a rational sphere, we combine two important ideas from previous work. The first involves proving the existence of fixed-point components
![]() $N_{i}$
of isometries that are rational spheres (see [Reference KennardKen14]). Smith theoretic results then imply restrictions on the components of
$N_{i}$
of isometries that are rational spheres (see [Reference KennardKen14]). Smith theoretic results then imply restrictions on the components of
![]() $M^{T}$
. The second main idea is to control the number of components of
$M^{T}$
. The second main idea is to control the number of components of
![]() $M^{T}$
that these submanifolds
$M^{T}$
that these submanifolds
![]() $N_{i}$
contain (see [Reference Amann and KennardAK14]).
$N_{i}$
contain (see [Reference Amann and KennardAK14]).
We conclude by remarking on the assumption that
![]() $b_{4}(M)=0$
. In the presence of positive curvature and torus symmetry as in Theorem A, the only other possibility is
$b_{4}(M)=0$
. In the presence of positive curvature and torus symmetry as in Theorem A, the only other possibility is
![]() $b_{4}(M)=1$
. Since our results when
$b_{4}(M)=1$
. Since our results when
![]() $b_{4}(M)=0$
suggest that
$b_{4}(M)=0$
suggest that
![]() $M$
might be a rational sphere, one might similarly hope to show that
$M$
might be a rational sphere, one might similarly hope to show that
![]() $b_{4}(M)=1$
implies that
$b_{4}(M)=1$
implies that
![]() $M$
has the rational type of a projective space. In particular, one might hope to calculate the Euler characteristic and signature of such a manifold.
$M$
has the rational type of a projective space. In particular, one might hope to calculate the Euler characteristic and signature of such a manifold.
1 Preliminaries
The main tool for proving Theorem A is the following proposition. This section is devoted to its proof.
Proposition 1.1. Let
![]() $M^{n}$
be a closed, positively curved Riemannian manifold with
$M^{n}$
be a closed, positively curved Riemannian manifold with
![]() $n\geqslant 21$
. Assume
$n\geqslant 21$
. Assume
![]() $T^{s}$
acts effectively by isometries on
$T^{s}$
acts effectively by isometries on
![]() $M$
with
$M$
with
![]() $s\geqslant \log _{4/3}(n-3)$
. If
$s\geqslant \log _{4/3}(n-3)$
. If
![]() $x$
and
$x$
and
![]() $y$
are fixed by
$y$
are fixed by
![]() $T^{s}$
, and if
$T^{s}$
, and if
![]() $M$
is not rationally
$M$
is not rationally
![]() $4$
-periodic, then there exist an involution
$4$
-periodic, then there exist an involution
![]() $\unicode[STIX]{x1D704}\in T^{s}$
and a component
$\unicode[STIX]{x1D704}\in T^{s}$
and a component
![]() $N\subseteq M^{\unicode[STIX]{x1D704}}$
such that
$N\subseteq M^{\unicode[STIX]{x1D704}}$
such that
![]() $(n-4)/4<\operatorname{cod}(N)\leqslant (n-4)/2$
,
$(n-4)/4<\operatorname{cod}(N)\leqslant (n-4)/2$
,
![]() $\dim \ker (T|_{N})\leqslant 1$
, and
$\dim \ker (T|_{N})\leqslant 1$
, and
![]() $x,y\in N$
.
$x,y\in N$
.
Here,
![]() $M^{\unicode[STIX]{x1D704}}$
denotes the fixed-point set of
$M^{\unicode[STIX]{x1D704}}$
denotes the fixed-point set of
![]() $\unicode[STIX]{x1D704}\in T$
,
$\unicode[STIX]{x1D704}\in T$
,
![]() $M_{x}^{\unicode[STIX]{x1D704}}$
the component of
$M_{x}^{\unicode[STIX]{x1D704}}$
the component of
![]() $M^{\unicode[STIX]{x1D704}}$
containing
$M^{\unicode[STIX]{x1D704}}$
containing
![]() $x$
, and
$x$
, and
![]() $\ker (T|_{M_{x}^{\unicode[STIX]{x1D704}}})$
the kernel of the induced
$\ker (T|_{M_{x}^{\unicode[STIX]{x1D704}}})$
the kernel of the induced
![]() $T$
-action on
$T$
-action on
![]() $M_{x}^{\unicode[STIX]{x1D704}}$
. For the definition of periodic cohomology in this context, see [Reference Amann and KennardAK14, Definition 1.8]. (The only fact we will use later is that a rationally
$M_{x}^{\unicode[STIX]{x1D704}}$
. For the definition of periodic cohomology in this context, see [Reference Amann and KennardAK14, Definition 1.8]. (The only fact we will use later is that a rationally
![]() $4$
-periodic manifold
$4$
-periodic manifold
![]() $M$
with
$M$
with
![]() $b_{4}(M)=0$
is a rational sphere.)
$b_{4}(M)=0$
is a rational sphere.)
The proof of Proposition 1.1 requires two technical lemmas. The first is a refinement of the proof setup for [Reference Amann and KennardAK14, Theorem A].
Lemma 1.2. Let
![]() $M$
be a closed, simply connected, positively curved Riemannian
$M$
be a closed, simply connected, positively curved Riemannian
![]() $n$
-manifold, let
$n$
-manifold, let
![]() $T$
be a torus acting effectively on
$T$
be a torus acting effectively on
![]() $M$
, and let
$M$
, and let
![]() $x$
be a fixed point. Fix
$x$
be a fixed point. Fix
![]() $c\geqslant 1$
,
$c\geqslant 1$
,
![]() $k_{0}\leqslant (n-c)/4$
, and some subset
$k_{0}\leqslant (n-c)/4$
, and some subset
![]() $A\subseteq M^{T}$
. Set
$A\subseteq M^{T}$
. Set
![]() $j=\lfloor \log _{2}(k_{0})\rfloor +1$
or
$j=\lfloor \log _{2}(k_{0})\rfloor +1$
or
![]() $j=\lfloor \log _{2}(k_{0})\rfloor$
according to whether
$j=\lfloor \log _{2}(k_{0})\rfloor$
according to whether
![]() $n$
is even or odd. If there exist independent involutions
$n$
is even or odd. If there exist independent involutions
![]() $\unicode[STIX]{x1D704}_{1},\ldots ,\unicode[STIX]{x1D704}_{j}\in T$
such that
$\unicode[STIX]{x1D704}_{1},\ldots ,\unicode[STIX]{x1D704}_{j}\in T$
such that
![]() $M_{x}^{\unicode[STIX]{x1D704}_{i}}$
contains
$M_{x}^{\unicode[STIX]{x1D704}_{i}}$
contains
![]() $A$
and has codimension at most
$A$
and has codimension at most
![]() $(n-c)/2$
for all
$(n-c)/2$
for all
![]() $i$
, then one of the following holds:
$i$
, then one of the following holds:
-
∙
 $M$
has
$M$
has
 $4$
-periodic rational cohomology; or
$4$
-periodic rational cohomology; or -
∙ there exists an involution
 $\unicode[STIX]{x1D704}\in T^{s}$
such that
$\unicode[STIX]{x1D704}\in T^{s}$
such that
 $A\subseteq M_{x}^{\unicode[STIX]{x1D704}}$
,
$A\subseteq M_{x}^{\unicode[STIX]{x1D704}}$
,
 $k_{0}<\operatorname{cod}(M_{x}^{\unicode[STIX]{x1D704}})\leqslant (n-c)/2$
, and
$k_{0}<\operatorname{cod}(M_{x}^{\unicode[STIX]{x1D704}})\leqslant (n-c)/2$
, and
 $\dim \ker (T|_{M_{x}^{\unicode[STIX]{x1D704}}})\leqslant 1$
.
$\dim \ker (T|_{M_{x}^{\unicode[STIX]{x1D704}}})\leqslant 1$
.
Proof. Assume that the second conclusion does not hold. Note that, if some involution
![]() $\unicode[STIX]{x1D704}\in T$
satisfies
$\unicode[STIX]{x1D704}\in T$
satisfies
![]() $\operatorname{cod}(M_{x}^{\unicode[STIX]{x1D704}})\leqslant (n-c)/2$
and
$\operatorname{cod}(M_{x}^{\unicode[STIX]{x1D704}})\leqslant (n-c)/2$
and
![]() $\dim \ker (T|_{M_{x}^{\unicode[STIX]{x1D704}}})\geqslant 2$
, then
$\dim \ker (T|_{M_{x}^{\unicode[STIX]{x1D704}}})\geqslant 2$
, then
![]() $M$
is rationally
$M$
is rationally
![]() $4$
-periodic by [Reference Amann and KennardAK14, Proposition 2.2]. In particular, we may assume that every involution
$4$
-periodic by [Reference Amann and KennardAK14, Proposition 2.2]. In particular, we may assume that every involution
![]() $\unicode[STIX]{x1D704}\in T$
with
$\unicode[STIX]{x1D704}\in T$
with
![]() $A\subseteq M_{x}^{\unicode[STIX]{x1D704}}$
and
$A\subseteq M_{x}^{\unicode[STIX]{x1D704}}$
and
![]() $\operatorname{cod}(M_{x}^{\unicode[STIX]{x1D704}})\leqslant (n-c)/2$
actually has
$\operatorname{cod}(M_{x}^{\unicode[STIX]{x1D704}})\leqslant (n-c)/2$
actually has
![]() $\operatorname{cod}(M_{x}^{\unicode[STIX]{x1D704}})\leqslant k_{0}$
.
$\operatorname{cod}(M_{x}^{\unicode[STIX]{x1D704}})\leqslant k_{0}$
.
In particular, we may assume that
![]() $\unicode[STIX]{x1D704}_{i}$
satisfies
$\unicode[STIX]{x1D704}_{i}$
satisfies
![]() $A\subseteq M_{x}^{\unicode[STIX]{x1D704}_{i}}$
and
$A\subseteq M_{x}^{\unicode[STIX]{x1D704}_{i}}$
and
![]() $\operatorname{cod}(M_{x}^{\unicode[STIX]{x1D704}_{i}})\leqslant k_{0}$
for all
$\operatorname{cod}(M_{x}^{\unicode[STIX]{x1D704}_{i}})\leqslant k_{0}$
for all
![]() $i$
. We claim that
$i$
. We claim that
![]() $\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}$
satisfies these two properties any time
$\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}$
satisfies these two properties any time
![]() $\unicode[STIX]{x1D70E}$
and
$\unicode[STIX]{x1D70E}$
and
![]() $\unicode[STIX]{x1D70F}$
do, where
$\unicode[STIX]{x1D70F}$
do, where
![]() $\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70F}\in \langle \unicode[STIX]{x1D704}_{1},\ldots ,\unicode[STIX]{x1D704}_{j}\rangle$
. Indeed, given any such
$\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70F}\in \langle \unicode[STIX]{x1D704}_{1},\ldots ,\unicode[STIX]{x1D704}_{j}\rangle$
. Indeed, given any such
![]() $\unicode[STIX]{x1D70E}$
and
$\unicode[STIX]{x1D70E}$
and
![]() $\unicode[STIX]{x1D70F}$
, we have
$\unicode[STIX]{x1D70F}$
, we have
Moreover, by Wilking’s connectedness lemma (see [Reference WilkingWil03, Theorem 2.1]),
![]() $M_{x}^{\unicode[STIX]{x1D70E}}\cap M_{x}^{\unicode[STIX]{x1D70F}}$
is connected, so
$M_{x}^{\unicode[STIX]{x1D70E}}\cap M_{x}^{\unicode[STIX]{x1D70F}}$
is connected, so
Since
![]() $M_{x}^{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}$
contains
$M_{x}^{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70F}}$
contains
![]() $A$
and has codimension at most
$A$
and has codimension at most
![]() $(n-c)/2$
, it actually has codimension at most
$(n-c)/2$
, it actually has codimension at most
![]() $k_{0}$
, so the proof of the claim is complete.
$k_{0}$
, so the proof of the claim is complete.
With the claim established, it follows that every
![]() $\unicode[STIX]{x1D70E}\in \langle \unicode[STIX]{x1D704}_{1},\ldots ,\unicode[STIX]{x1D704}_{j}\rangle$
satisfies
$\unicode[STIX]{x1D70E}\in \langle \unicode[STIX]{x1D704}_{1},\ldots ,\unicode[STIX]{x1D704}_{j}\rangle$
satisfies
![]() $\operatorname{cod}(M_{x}^{\unicode[STIX]{x1D70E}})\leqslant k_{0}$
. We conclude the proof as in the proof of [Reference Amann and KennardAK14, Proposition 2.1]. There is only one modification. In the notation of that proof, the codimension
$\operatorname{cod}(M_{x}^{\unicode[STIX]{x1D70E}})\leqslant k_{0}$
. We conclude the proof as in the proof of [Reference Amann and KennardAK14, Proposition 2.1]. There is only one modification. In the notation of that proof, the codimension
![]() $k_{j}$
is estimated as follows:
$k_{j}$
is estimated as follows:
In our case,
![]() $k_{1}\leqslant k_{0}$
, and the definition of
$k_{1}\leqslant k_{0}$
, and the definition of
![]() $j$
implies that
$j$
implies that
![]() $k_{j}<2$
if
$k_{j}<2$
if
![]() $n$
is even and
$n$
is even and
![]() $k_{j}<4$
if
$k_{j}<4$
if
![]() $n$
is odd. If, in fact,
$n$
is odd. If, in fact,
![]() $k_{j}=0$
, then the proof concludes as in [Reference Amann and KennardAK14]. Otherwise,
$k_{j}=0$
, then the proof concludes as in [Reference Amann and KennardAK14]. Otherwise,
![]() $k_{j}=2$
and
$k_{j}=2$
and
![]() $n$
is odd. It is an easy consequence of Wilking’s connectedness theorem to show in this case that
$n$
is odd. It is an easy consequence of Wilking’s connectedness theorem to show in this case that
![]() $N_{j}$
is a rational sphere and hence rationally
$N_{j}$
is a rational sphere and hence rationally
![]() $4$
-periodic. One then proceeds again as in the cited proof, using the connectedness lemma to lift the property of being rationally
$4$
-periodic. One then proceeds again as in the cited proof, using the connectedness lemma to lift the property of being rationally
![]() $4$
-periodic up to
$4$
-periodic up to
![]() $M$
.◻
$M$
.◻
To apply Lemma 1.2, one must prove the existence of the involutions
![]() $\unicode[STIX]{x1D704}_{1},\ldots ,\unicode[STIX]{x1D704}_{j}$
. To do this, we generalize [Reference Amann and KennardAK14, Proposition 2.4].
$\unicode[STIX]{x1D704}_{1},\ldots ,\unicode[STIX]{x1D704}_{j}$
. To do this, we generalize [Reference Amann and KennardAK14, Proposition 2.4].
Lemma 1.3. Let
![]() $n\geqslant c\geqslant 0$
and
$n\geqslant c\geqslant 0$
and
![]() $j\geqslant 1$
. Let
$j\geqslant 1$
. Let
![]() $M^{n}$
be a closed, positively curved Riemannian manifold, assume
$M^{n}$
be a closed, positively curved Riemannian manifold, assume
![]() $T^{s}$
acts effectively by isometries on
$T^{s}$
acts effectively by isometries on
![]() $M$
, and let
$M$
, and let
![]() $x_{1},\ldots ,x_{t}\in M$
be fixed points. If
$x_{1},\ldots ,x_{t}\in M$
be fixed points. If
then there exist independent involutions
![]() $\unicode[STIX]{x1D704}_{1},\ldots ,\unicode[STIX]{x1D704}_{j}\in T^{s}$
such that, for all
$\unicode[STIX]{x1D704}_{1},\ldots ,\unicode[STIX]{x1D704}_{j}\in T^{s}$
such that, for all
![]() $1\leqslant i\leqslant j$
, the maximal component of
$1\leqslant i\leqslant j$
, the maximal component of
![]() $M^{\unicode[STIX]{x1D704}_{i}}$
has codimension at most
$M^{\unicode[STIX]{x1D704}_{i}}$
has codimension at most
![]() $(n-c)/2$
and contains at least
$(n-c)/2$
and contains at least
![]() $\lceil (t+1)/2\rceil$
of the points
$\lceil (t+1)/2\rceil$
of the points
![]() $x_{1},\ldots ,x_{t}$
.
$x_{1},\ldots ,x_{t}$
.
Proof. Set
![]() $m=\lfloor n/2\rfloor$
. For each
$m=\lfloor n/2\rfloor$
. For each
![]() $x_{i}$
, choose a basis of
$x_{i}$
, choose a basis of
![]() $T_{x_{i}}M$
such that the image of every
$T_{x_{i}}M$
such that the image of every
![]() $\unicode[STIX]{x1D704}\in \mathbb{Z}_{2}^{s}\subseteq T^{s}$
under the isotropy representation takes the form
$\unicode[STIX]{x1D704}\in \mathbb{Z}_{2}^{s}\subseteq T^{s}$
under the isotropy representation takes the form
![]() $\operatorname{diag}(\unicode[STIX]{x1D716}_{1}I,\ldots ,\unicode[STIX]{x1D716}_{m}I)$
or
$\operatorname{diag}(\unicode[STIX]{x1D716}_{1}I,\ldots ,\unicode[STIX]{x1D716}_{m}I)$
or
![]() $\operatorname{diag}(\unicode[STIX]{x1D716}_{1}I,\ldots ,\unicode[STIX]{x1D716}_{m}I,1)$
according to whether
$\operatorname{diag}(\unicode[STIX]{x1D716}_{1}I,\ldots ,\unicode[STIX]{x1D716}_{m}I,1)$
according to whether
![]() $n$
is even or odd. Here, the
$n$
is even or odd. Here, the
![]() $\unicode[STIX]{x1D716}_{i}=\pm 1$
, and
$\unicode[STIX]{x1D716}_{i}=\pm 1$
, and
![]() $I$
denotes the
$I$
denotes the
![]() $2\times 2$
identity matrix. Observe that
$2\times 2$
identity matrix. Observe that
![]() $\operatorname{cod}(M_{x_{i}}^{\unicode[STIX]{x1D704}})$
equals twice the Hamming weight of
$\operatorname{cod}(M_{x_{i}}^{\unicode[STIX]{x1D704}})$
equals twice the Hamming weight of
![]() $(\unicode[STIX]{x1D716}_{1},\ldots ,\unicode[STIX]{x1D716}_{m})\in \mathbb{Z}_{2}^{m}$
.
$(\unicode[STIX]{x1D716}_{1},\ldots ,\unicode[STIX]{x1D716}_{m})\in \mathbb{Z}_{2}^{m}$
.
The direct sum of these
![]() $t$
maps induces a homomorphism
$t$
maps induces a homomorphism
![]() $\unicode[STIX]{x1D719}:\mathbb{Z}_{2}^{s}\rightarrow \bigoplus _{i=1}^{t}\mathbb{Z}_{2}^{m}\cong \mathbb{Z}_{2}^{tm}$
. Let
$\unicode[STIX]{x1D719}:\mathbb{Z}_{2}^{s}\rightarrow \bigoplus _{i=1}^{t}\mathbb{Z}_{2}^{m}\cong \mathbb{Z}_{2}^{tm}$
. Let
![]() $\unicode[STIX]{x1D719}_{u}$
denote the composition of
$\unicode[STIX]{x1D719}_{u}$
denote the composition of
![]() $\unicode[STIX]{x1D719}$
with the projection onto the
$\unicode[STIX]{x1D719}$
with the projection onto the
![]() $u$
th component. For example, the codimension of
$u$
th component. For example, the codimension of
![]() $M_{x_{1}}^{\unicode[STIX]{x1D704}}$
is equal to twice the Hamming weight of the vector
$M_{x_{1}}^{\unicode[STIX]{x1D704}}$
is equal to twice the Hamming weight of the vector
![]() $(\unicode[STIX]{x1D719}_{1}(\unicode[STIX]{x1D704}),\ldots ,\unicode[STIX]{x1D719}_{m}(\unicode[STIX]{x1D704}))\in \mathbb{Z}_{2}^{m}$
.
$(\unicode[STIX]{x1D719}_{1}(\unicode[STIX]{x1D704}),\ldots ,\unicode[STIX]{x1D719}_{m}(\unicode[STIX]{x1D704}))\in \mathbb{Z}_{2}^{m}$
.
Consider now an integer
![]() $0\leqslant h\leqslant j-1$
such that there exist independent
$0\leqslant h\leqslant j-1$
such that there exist independent
![]() $\unicode[STIX]{x1D704}_{1},\ldots ,\unicode[STIX]{x1D704}_{h}\in \mathbb{Z}_{2}^{s}$
and integers
$\unicode[STIX]{x1D704}_{1},\ldots ,\unicode[STIX]{x1D704}_{h}\in \mathbb{Z}_{2}^{s}$
and integers
![]() $u_{1},\ldots ,u_{h}$
such that, for all
$u_{1},\ldots ,u_{h}$
such that, for all
![]() $1\leqslant i\leqslant h$
:
$1\leqslant i\leqslant h$
:
-
(1) there is a component
 $N_{i}$
of
$N_{i}$
of
 $M^{\unicode[STIX]{x1D704}_{i}}$
with codimension at most
$M^{\unicode[STIX]{x1D704}_{i}}$
with codimension at most
 $(n-c)/2$
that contains at least
$(n-c)/2$
that contains at least
 $\lceil (t+1)/2\rceil$
of the points
$\lceil (t+1)/2\rceil$
of the points
 $x_{1},\ldots ,x_{t}$
;
$x_{1},\ldots ,x_{t}$
; -
(2)
 $\unicode[STIX]{x1D719}_{u_{i}}(\unicode[STIX]{x1D704}_{i})\in \mathbb{Z}_{2}$
is non-trivial; and
$\unicode[STIX]{x1D719}_{u_{i}}(\unicode[STIX]{x1D704}_{i})\in \mathbb{Z}_{2}$
is non-trivial; and -
(3)
 $\unicode[STIX]{x1D719}_{u_{i^{\prime }}}(\unicode[STIX]{x1D704}_{i})\in \mathbb{Z}_{2}$
is trivial for all
$\unicode[STIX]{x1D719}_{u_{i^{\prime }}}(\unicode[STIX]{x1D704}_{i})\in \mathbb{Z}_{2}$
is trivial for all
 $1\leqslant i^{\prime }<i$
.
$1\leqslant i^{\prime }<i$
.
Note that these conditions are vacuously satisfied for
![]() $h=0$
. We claim that, given
$h=0$
. We claim that, given
![]() $\unicode[STIX]{x1D704}_{1},\ldots ,\unicode[STIX]{x1D704}_{h}$
as above, there exists
$\unicode[STIX]{x1D704}_{1},\ldots ,\unicode[STIX]{x1D704}_{h}$
as above, there exists
![]() $\unicode[STIX]{x1D704}_{h+1}$
such that all of these properties hold. By induction, this suffices to prove the existence of
$\unicode[STIX]{x1D704}_{h+1}$
such that all of these properties hold. By induction, this suffices to prove the existence of
![]() $\unicode[STIX]{x1D704}_{1},\ldots ,\unicode[STIX]{x1D704}_{j}$
as in the conclusion of the lemma.
$\unicode[STIX]{x1D704}_{1},\ldots ,\unicode[STIX]{x1D704}_{j}$
as in the conclusion of the lemma.
To start, choose a
![]() $\mathbb{Z}_{2}^{s-h}\subseteq \ker (\unicode[STIX]{x1D719}_{u_{1}})\cap \cdots \cap \ker (\unicode[STIX]{x1D719}_{u_{h}})\subseteq \mathbb{Z}_{2}^{s}$
. Note that every
$\mathbb{Z}_{2}^{s-h}\subseteq \ker (\unicode[STIX]{x1D719}_{u_{1}})\cap \cdots \cap \ker (\unicode[STIX]{x1D719}_{u_{h}})\subseteq \mathbb{Z}_{2}^{s}$
. Note that every
![]() $\unicode[STIX]{x1D704}\in \mathbb{Z}_{2}^{s-h}$
automatically satisfies the last condition above. Moreover, every non-trivial
$\unicode[STIX]{x1D704}\in \mathbb{Z}_{2}^{s-h}$
automatically satisfies the last condition above. Moreover, every non-trivial
![]() $\unicode[STIX]{x1D704}\in \mathbb{Z}_{2}^{s-h}$
is independent of
$\unicode[STIX]{x1D704}\in \mathbb{Z}_{2}^{s-h}$
is independent of
![]() $\unicode[STIX]{x1D704}_{1},\ldots ,\unicode[STIX]{x1D704}_{h}$
and is non-trivial since the
$\unicode[STIX]{x1D704}_{1},\ldots ,\unicode[STIX]{x1D704}_{h}$
and is non-trivial since the
![]() $T^{s}$
action is effective. It therefore suffices to prove that some
$T^{s}$
action is effective. It therefore suffices to prove that some
![]() $\unicode[STIX]{x1D704}\in \mathbb{Z}_{2}^{s-h}$
has a fixed-point component with codimension at most
$\unicode[STIX]{x1D704}\in \mathbb{Z}_{2}^{s-h}$
has a fixed-point component with codimension at most
![]() $(n-c)/2$
that contains
$(n-c)/2$
that contains
![]() $\lceil (t+1)/2\rceil$
of the
$\lceil (t+1)/2\rceil$
of the
![]() $x_{1},\ldots ,x_{t}$
.
$x_{1},\ldots ,x_{t}$
.
Consider the composition
where the last map projects away the
![]() $u_{i}$
th components for
$u_{i}$
th components for
![]() $1\leqslant i\leqslant h$
. By the choice of the
$1\leqslant i\leqslant h$
. By the choice of the
![]() $u_{i}$
, the Hamming weight of the image of
$u_{i}$
, the Hamming weight of the image of
![]() $\unicode[STIX]{x1D704}\in \mathbb{Z}_{2}^{s-h}$
under this composition is half of the sum of the codimensions
$\unicode[STIX]{x1D704}\in \mathbb{Z}_{2}^{s-h}$
under this composition is half of the sum of the codimensions
![]() $k_{i}=\operatorname{cod}(M_{x_{i}}^{\unicode[STIX]{x1D704}})$
. As in the proof of [Reference Amann and KennardAK14, Proposition 2.4], an argument based on Frankel’s theorem implies the following. If
$k_{i}=\operatorname{cod}(M_{x_{i}}^{\unicode[STIX]{x1D704}})$
. As in the proof of [Reference Amann and KennardAK14, Proposition 2.4], an argument based on Frankel’s theorem implies the following. If
![]() $\unicode[STIX]{x1D704}\in \mathbb{Z}_{2}^{s-h}$
exists such that
$\unicode[STIX]{x1D704}\in \mathbb{Z}_{2}^{s-h}$
exists such that
![]() $\sum _{i=1}^{t}k_{i}\leqslant t(n-c)/2$
, then there exists a component of
$\sum _{i=1}^{t}k_{i}\leqslant t(n-c)/2$
, then there exists a component of
![]() $M^{\unicode[STIX]{x1D704}}$
with codimension at most
$M^{\unicode[STIX]{x1D704}}$
with codimension at most
![]() $(n-c)/2$
that contains
$(n-c)/2$
that contains
![]() $\lceil (t+1)/2\rceil$
of the
$\lceil (t+1)/2\rceil$
of the
![]() $x_{1},\ldots ,x_{t}$
. It therefore suffices to prove that some non-trivial
$x_{1},\ldots ,x_{t}$
. It therefore suffices to prove that some non-trivial
![]() $\unicode[STIX]{x1D704}\in \mathbb{Z}_{2}^{s-h}$
exists whose image under the above map
$\unicode[STIX]{x1D704}\in \mathbb{Z}_{2}^{s-h}$
exists whose image under the above map
![]() $\mathbb{Z}_{2}^{s-h}\rightarrow \mathbb{Z}_{2}^{tm-h}$
has weight at most
$\mathbb{Z}_{2}^{s-h}\rightarrow \mathbb{Z}_{2}^{tm-h}$
has weight at most
![]() $t(n-c)/4$
.
$t(n-c)/4$
.
If no such involution exists, the Griesmer bound (see, for example, the proof of [Reference Amann and KennardAK14, Proposition 2.4]) implies that
Since every summand on the right-hand side is at least one, this inequality is preserved if we replace
![]() $h$
by
$h$
by
![]() $h+1$
. Inductively, this inequality is preserved if we replace
$h+1$
. Inductively, this inequality is preserved if we replace
![]() $h$
by
$h$
by
![]() $j-1$
. On the other hand, this contradicts inequality (1.1), so the proof is complete.◻
$j-1$
. On the other hand, this contradicts inequality (1.1), so the proof is complete.◻
With Lemmas 1.2 and 1.3 established, Proposition 1.1 is an easy consequence.
Proof of Proposition 1.1.
Set
![]() $c=4$
,
$c=4$
,
![]() $k_{0}=(n-4)/4$
, and
$k_{0}=(n-4)/4$
, and
![]() $j=\lfloor \log _{2}(k_{0})\rfloor +1-\unicode[STIX]{x1D716}$
, where
$j=\lfloor \log _{2}(k_{0})\rfloor +1-\unicode[STIX]{x1D716}$
, where
![]() $\unicode[STIX]{x1D716}$
is zero or one according to whether
$\unicode[STIX]{x1D716}$
is zero or one according to whether
![]() $n$
is even or odd. By Lemma 1.2, it suffices to prove the existence of independent involutions
$n$
is even or odd. By Lemma 1.2, it suffices to prove the existence of independent involutions
![]() $\unicode[STIX]{x1D704}_{1},\ldots ,\unicode[STIX]{x1D704}_{j}\in T^{s}$
such that each
$\unicode[STIX]{x1D704}_{1},\ldots ,\unicode[STIX]{x1D704}_{j}\in T^{s}$
such that each
![]() $M^{\unicode[STIX]{x1D704}_{i}}$
has a component of codimension at most
$M^{\unicode[STIX]{x1D704}_{i}}$
has a component of codimension at most
![]() $k_{0}$
that contains both
$k_{0}$
that contains both
![]() $x$
and
$x$
and
![]() $y$
.
$y$
.
Set
![]() $t=2$
, and note that
$t=2$
, and note that
![]() $\lceil (t+1)/2\rceil =2$
. By Lemma 1.3, such a collection of involutions exists if inequality (1.1) holds. To verify this inequality for all
$\lceil (t+1)/2\rceil =2$
. By Lemma 1.3, such a collection of involutions exists if inequality (1.1) holds. To verify this inequality for all
![]() $n\geqslant 21$
, first observe that
$n\geqslant 21$
, first observe that
and hence that
![]() $\lceil (n-3)/2^{i+1}\rceil =1$
for all
$\lceil (n-3)/2^{i+1}\rceil =1$
for all
![]() $i\geqslant s-j$
. In particular, we can estimate the right-hand side, denoted by
$i\geqslant s-j$
. In particular, we can estimate the right-hand side, denoted by
![]() $R$
, of inequality (1.1) as follows. First,
$R$
, of inequality (1.1) as follows. First,
Second, note that
![]() $s\geqslant 6$
, hence
$s\geqslant 6$
, hence
since
![]() $s-5>\log _{2}(n-3)$
. This proves that inequality (1.1) holds.◻
$s-5>\log _{2}(n-3)$
. This proves that inequality (1.1) holds.◻
2 Proof of Theorem A
For an isometric action by a torus
![]() $T$
on a Riemannian manifold
$T$
on a Riemannian manifold
![]() $M$
, the fixed-point set
$M$
, the fixed-point set
![]() $M^{T}$
is a union of closed, oriented, totally geodesic submanifolds of even codimension. By Synge’s theorem, each component of
$M^{T}$
is a union of closed, oriented, totally geodesic submanifolds of even codimension. By Synge’s theorem, each component of
![]() $M^{T}$
is simply connected when
$M^{T}$
is simply connected when
![]() $M$
has positive sectional curvature. In addition, we recall the following results that relate the topology of
$M$
has positive sectional curvature. In addition, we recall the following results that relate the topology of
![]() $M$
and
$M$
and
![]() $M^{T}$
(see [Reference ConnerCon57] and [Reference Hirzebruch, Berger and JungHBJ92, p. 72]):
$M^{T}$
(see [Reference ConnerCon57] and [Reference Hirzebruch, Berger and JungHBJ92, p. 72]):
-
∙ the Euler characteristics satisfy
 $\unicode[STIX]{x1D712}(M)=\unicode[STIX]{x1D712}(M^{T})$
;
$\unicode[STIX]{x1D712}(M)=\unicode[STIX]{x1D712}(M^{T})$
; -
∙ the signatures satisfy
 $\unicode[STIX]{x1D70E}(M)=\unicode[STIX]{x1D70E}(M^{T})$
;
$\unicode[STIX]{x1D70E}(M)=\unicode[STIX]{x1D70E}(M^{T})$
; -
∙ (Conner) the even Betti numbers satisfy
 $\sum b_{2i}(M^{T})\leqslant \sum b_{2i}(M)$
, and likewise for the odd Betti numbers.
$\sum b_{2i}(M^{T})\leqslant \sum b_{2i}(M)$
, and likewise for the odd Betti numbers.
Note that, if
![]() $M$
is an even-dimensional, positively curved rational sphere, then
$M$
is an even-dimensional, positively curved rational sphere, then
![]() $M^{T}$
is as well. Since a positive- and even-dimensional sphere trivially has Euler characteristic two and signature zero, the first three conclusions of Theorem A are an immediate consequence of the following result (the fourth conclusion is proved at the end of the section).
$M^{T}$
is as well. Since a positive- and even-dimensional sphere trivially has Euler characteristic two and signature zero, the first three conclusions of Theorem A are an immediate consequence of the following result (the fourth conclusion is proved at the end of the section).
Theorem 2.1. Let
![]() $M^{n}$
be a closed, simply connected, positively curved Riemannian manifold with
$M^{n}$
be a closed, simply connected, positively curved Riemannian manifold with
![]() $b_{4}(M)=0$
. If a torus
$b_{4}(M)=0$
. If a torus
![]() $T$
acts effectively by isometries on
$T$
acts effectively by isometries on
![]() $M$
with
$M$
with
![]() $\dim (T)\geqslant \log _{4/3}(n-3)$
, then
$\dim (T)\geqslant \log _{4/3}(n-3)$
, then
![]() $M^{T}=N^{T}$
for some totally geodesic, even-codimensional, rational sphere
$M^{T}=N^{T}$
for some totally geodesic, even-codimensional, rational sphere
![]() $N\subseteq M$
to which the
$N\subseteq M$
to which the
![]() $T$
-action restricts. Moreover, if
$T$
-action restricts. Moreover, if
![]() $n$
is even, then
$n$
is even, then
![]() $N$
may be chosen to have positive dimension.
$N$
may be chosen to have positive dimension.
This result can be seen as a less localized version of the main theorem in [Reference KennardKen14]. Under the assumptions of Theorem 2.1, the results in [Reference KennardKen14] imply that each component of
![]() $M^{T}$
is a component of the fixed-point set of some
$M^{T}$
is a component of the fixed-point set of some
![]() $N$
as in this theorem. The novelty here is that the entire fixed-point set
$N$
as in this theorem. The novelty here is that the entire fixed-point set
![]() $M^{T}$
is contained in this submanifold
$M^{T}$
is contained in this submanifold
![]() $N$
.
$N$
.
The proof of Theorem 2.1 is by induction over the dimension in the style of Wilking [Reference WilkingWil03]. First, if
![]() $n\leqslant 3$
, the result is trivial since
$n\leqslant 3$
, the result is trivial since
![]() $M$
is a homotopy sphere. Second, if
$M$
is a homotopy sphere. Second, if
![]() $n=4$
, the result is vacuous since
$n=4$
, the result is vacuous since
![]() $b_{4}(M)=1$
in this case. Third, for
$b_{4}(M)=1$
in this case. Third, for
![]() $5\leqslant n\leqslant 20$
,
$5\leqslant n\leqslant 20$
,
![]() $s\geqslant n/2$
, hence the result of Grove and Searle implies that
$s\geqslant n/2$
, hence the result of Grove and Searle implies that
![]() $M$
is diffeomorphic to the sphere (see [Reference Grove and SearleGS94]). In particular,
$M$
is diffeomorphic to the sphere (see [Reference Grove and SearleGS94]). In particular,
![]() $M$
is a rational sphere, so the conclusion of the theorem holds by taking
$M$
is a rational sphere, so the conclusion of the theorem holds by taking
![]() $N=M$
.
$N=M$
.
Finally, suppose that
![]() $n\geqslant 21$
. As in the previous paragraph, if
$n\geqslant 21$
. As in the previous paragraph, if
![]() $M$
itself is a rational sphere, then the theorem immediately holds. We assume throughout that
$M$
itself is a rational sphere, then the theorem immediately holds. We assume throughout that
![]() $M$
is not a rational sphere. Since
$M$
is not a rational sphere. Since
![]() $b_{4}(M)=0$
, this is equivalent to assuming that
$b_{4}(M)=0$
, this is equivalent to assuming that
![]() $M$
does not have
$M$
does not have
![]() $4$
-periodic rational cohomology. The induction step has two parts. The first considers the case where some component
$4$
-periodic rational cohomology. The induction step has two parts. The first considers the case where some component
![]() $M_{x}^{T}$
has positive dimension.
$M_{x}^{T}$
has positive dimension.
Lemma 2.2. If some component
![]() $M_{x}^{T}$
of
$M_{x}^{T}$
of
![]() $M^{T}$
has positive dimension, then
$M^{T}$
has positive dimension, then
![]() $M^{T}=M_{x}^{T}$
and is a rational sphere. In particular, the theorem holds with
$M^{T}=M_{x}^{T}$
and is a rational sphere. In particular, the theorem holds with
![]() $N=M^{T}$
.
$N=M^{T}$
.
Proof. Let
![]() $y\in M^{T}$
. By Proposition 1.1, there exist an
$y\in M^{T}$
. By Proposition 1.1, there exist an
![]() $\unicode[STIX]{x1D704}\in T$
and a component
$\unicode[STIX]{x1D704}\in T$
and a component
![]() $N\subseteq M^{\unicode[STIX]{x1D704}}$
such that
$N\subseteq M^{\unicode[STIX]{x1D704}}$
such that
![]() $(n-4)/4<\operatorname{cod}(N)\leqslant (n-4)/2$
,
$(n-4)/4<\operatorname{cod}(N)\leqslant (n-4)/2$
,
![]() $\dim \ker (T|_{N})\leqslant 1$
, and
$\dim \ker (T|_{N})\leqslant 1$
, and
![]() $x,y\in N$
. By Wilking’s connectedness lemma,
$x,y\in N$
. By Wilking’s connectedness lemma,
![]() $N$
is simply connected and
$N$
is simply connected and
![]() $b_{4}(N)=0$
. Moreover, since
$b_{4}(N)=0$
. Moreover, since
![]() $\operatorname{cod}(N)\geqslant (n-3)/4$
,
$\operatorname{cod}(N)\geqslant (n-3)/4$
,
Since
![]() $T/\text{ker}(T|_{N})$
is a torus that acts effectively on
$T/\text{ker}(T|_{N})$
is a torus that acts effectively on
![]() $N$
, a closed, simply connected, positively curved Riemannian manifold with
$N$
, a closed, simply connected, positively curved Riemannian manifold with
![]() $b_{4}(N)=0$
, the induction hypothesis applies to
$b_{4}(N)=0$
, the induction hypothesis applies to
![]() $N$
. Since
$N$
. Since
![]() $M_{x}^{T}$
and
$M_{x}^{T}$
and
![]() $M_{y}^{T}$
are components of
$M_{y}^{T}$
are components of
![]() $N^{T}=N\cap M^{T}$
, we therefore have
$N^{T}=N\cap M^{T}$
, we therefore have
Observe that
![]() $\sum b_{i}(M_{x}^{T})\geqslant 2$
since
$\sum b_{i}(M_{x}^{T})\geqslant 2$
since
![]() $M_{x}^{T}$
has positive dimension. In particular, if
$M_{x}^{T}$
has positive dimension. In particular, if
![]() $y$
lies in a component of
$y$
lies in a component of
![]() $M^{T}$
different from
$M^{T}$
different from
![]() $M_{x}^{T}$
, then the the left-hand side is at least
$M_{x}^{T}$
, then the the left-hand side is at least
a contradiction. This shows that
![]() $M^{T}=M_{x}^{T}$
. Moreover, the above argument works with
$M^{T}=M_{x}^{T}$
. Moreover, the above argument works with
![]() $x=y$
, hence
$x=y$
, hence
![]() $\sum b_{i}(M_{x}^{T})=2$
, which implies that
$\sum b_{i}(M_{x}^{T})=2$
, which implies that
![]() $M_{x}^{T}$
is a rational sphere.◻
$M_{x}^{T}$
is a rational sphere.◻
The other possibility is that
![]() $T$
has only isolated fixed points.
$T$
has only isolated fixed points.
Lemma 2.3. If
![]() $\dim (M^{T})=0$
, then there are exactly two isolated fixed points. Moreover, there exists a totally geodesic, positive-dimensional, and even-dimensional rational sphere
$\dim (M^{T})=0$
, then there are exactly two isolated fixed points. Moreover, there exists a totally geodesic, positive-dimensional, and even-dimensional rational sphere
![]() $N\subseteq M$
on which
$N\subseteq M$
on which
![]() $T$
acts such that
$T$
acts such that
![]() $M^{T}=N^{T}$
.
$M^{T}=N^{T}$
.
Proof. First, a theorem of Berger implies there is at least one fixed point (see [Reference BergerBer66]), and there cannot be exactly one fixed point (see Bredon [Reference BredonBre72, Corollary IV.2.3, p. 178]).
Suppose for a moment that
![]() $M^{T}$
has exactly two isolated fixed points. By Proposition 1.1,
$M^{T}$
has exactly two isolated fixed points. By Proposition 1.1,
![]() $M^{T}\subseteq P$
for some totally geodesic, even-dimensional, closed submanifold
$M^{T}\subseteq P$
for some totally geodesic, even-dimensional, closed submanifold
![]() $P$
with
$P$
with
![]() $b_{4}(P)=0$
and an isometric torus action of rank at least
$b_{4}(P)=0$
and an isometric torus action of rank at least
![]() $\log _{4/3}(\dim P-3)$
. By the induction hypothesis applied to
$\log _{4/3}(\dim P-3)$
. By the induction hypothesis applied to
![]() $P$
,
$P$
,
![]() $P^{T}=N^{T}$
for some totally geodesic, even-dimensional, positive-dimensional rational sphere
$P^{T}=N^{T}$
for some totally geodesic, even-dimensional, positive-dimensional rational sphere
![]() $N\subseteq P$
. Since
$N\subseteq P$
. Since
![]() $M^{T}\subseteq N^{T}\subseteq M^{T}$
, this proves the lemma in this case.
$M^{T}\subseteq N^{T}\subseteq M^{T}$
, this proves the lemma in this case.
Finally, suppose that
![]() $M^{T}$
has at least three (distinct) isolated fixed points,
$M^{T}$
has at least three (distinct) isolated fixed points,
![]() $x$
,
$x$
,
![]() $y$
, and
$y$
, and
![]() $z$
. Two applications of Proposition 1.1 imply the existence of involutions
$z$
. Two applications of Proposition 1.1 imply the existence of involutions
![]() $\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70F}\in T^{s}$
such that:
$\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70F}\in T^{s}$
such that:
-
∙
 $M_{x}^{\unicode[STIX]{x1D70E}}$
has
$M_{x}^{\unicode[STIX]{x1D70E}}$
has
 $\dim \ker (T|_{M_{x}^{\unicode[STIX]{x1D70E}}})\leqslant 1$
,
$\dim \ker (T|_{M_{x}^{\unicode[STIX]{x1D70E}}})\leqslant 1$
,
 $(n-4)/4<\operatorname{cod}(M_{x}^{\unicode[STIX]{x1D70E}})\leqslant (n-4)/2$
, and
$(n-4)/4<\operatorname{cod}(M_{x}^{\unicode[STIX]{x1D70E}})\leqslant (n-4)/2$
, and
 $y\in M_{x}^{\unicode[STIX]{x1D70E}}$
; and
$y\in M_{x}^{\unicode[STIX]{x1D70E}}$
; and -
∙
 $M_{x}^{\unicode[STIX]{x1D70F}}$
has
$M_{x}^{\unicode[STIX]{x1D70F}}$
has
 $\dim \ker (T|_{M_{x}^{\unicode[STIX]{x1D70F}}})\leqslant 1$
,
$\dim \ker (T|_{M_{x}^{\unicode[STIX]{x1D70F}}})\leqslant 1$
,
 $(n-4)/4<\operatorname{cod}(M_{x}^{\unicode[STIX]{x1D70F}})\leqslant (n-4)/2$
, and
$(n-4)/4<\operatorname{cod}(M_{x}^{\unicode[STIX]{x1D70F}})\leqslant (n-4)/2$
, and
 $z\in M_{x}^{\unicode[STIX]{x1D70E}}$
.
$z\in M_{x}^{\unicode[STIX]{x1D70E}}$
.
As before, the induction hypothesis applies to both
![]() $M_{x}^{\unicode[STIX]{x1D70E}}$
and
$M_{x}^{\unicode[STIX]{x1D70E}}$
and
![]() $M_{x}^{\unicode[STIX]{x1D70F}}$
. Since the torus action on
$M_{x}^{\unicode[STIX]{x1D70F}}$
. Since the torus action on
![]() $M$
has only isolated fixed points, the same is true of the torus action on
$M$
has only isolated fixed points, the same is true of the torus action on
![]() $M_{x}^{\unicode[STIX]{x1D70E}}$
and
$M_{x}^{\unicode[STIX]{x1D70E}}$
and
![]() $M_{x}^{\unicode[STIX]{x1D70F}}$
. Hence
$M_{x}^{\unicode[STIX]{x1D70F}}$
. Hence
![]() $(M_{x}^{\unicode[STIX]{x1D70E}})^{T}=\{x,y\}$
and
$(M_{x}^{\unicode[STIX]{x1D70E}})^{T}=\{x,y\}$
and
![]() $(M_{x}^{\unicode[STIX]{x1D70F}})^{T}=\{x,z\}$
. This further implies
$(M_{x}^{\unicode[STIX]{x1D70F}})^{T}=\{x,z\}$
. This further implies
On the other hand, Frankel’s theorem implies that
![]() $M_{x}^{\unicode[STIX]{x1D70E}}$
and
$M_{x}^{\unicode[STIX]{x1D70E}}$
and
![]() $M_{x}^{\unicode[STIX]{x1D70F}}$
intersect, and Wilking’s connectedness lemma implies that
$M_{x}^{\unicode[STIX]{x1D70F}}$
intersect, and Wilking’s connectedness lemma implies that
![]() $M_{x}^{\unicode[STIX]{x1D70E}}\cap M_{x}^{\unicode[STIX]{x1D70F}}$
is connected and simply connected. In particular, as with
$M_{x}^{\unicode[STIX]{x1D70E}}\cap M_{x}^{\unicode[STIX]{x1D70F}}$
is connected and simply connected. In particular, as with
![]() $M$
, this intersection cannot have exactly one fixed point. This concludes the proof.◻
$M$
, this intersection cannot have exactly one fixed point. This concludes the proof.◻
This concludes the proof of Theorem 2.1 and hence of the first three conclusions of Theorem A. We now prove the fourth conclusion.
Proof of Theorem A.
[Conclusion (d)] Let
![]() $g\in T$
. The Lefschetz number of the map
$g\in T$
. The Lefschetz number of the map
![]() $g:M\rightarrow M$
is equal to
$g:M\rightarrow M$
is equal to
![]() $\unicode[STIX]{x1D712}(M)$
since
$\unicode[STIX]{x1D712}(M)$
since
![]() $g$
is homotopic to the identity. Hence
$g$
is homotopic to the identity. Hence
![]() $\unicode[STIX]{x1D712}(M^{g})=\unicode[STIX]{x1D712}(M)=2$
, so
$\unicode[STIX]{x1D712}(M^{g})=\unicode[STIX]{x1D712}(M)=2$
, so
![]() $M^{g}$
is non-empty.
$M^{g}$
is non-empty.
Since
![]() $g:M\rightarrow M$
is orientation-preserving, each component of
$g:M\rightarrow M$
is orientation-preserving, each component of
![]() $M^{g}$
is a closed, even-dimensional, totally geodesic submanifold of
$M^{g}$
is a closed, even-dimensional, totally geodesic submanifold of
![]() $M$
to which the
$M$
to which the
![]() $T$
-action restricts. Hence each component of
$T$
-action restricts. Hence each component of
![]() $M^{g}$
contains a fixed point of
$M^{g}$
contains a fixed point of
![]() $T$
by Berger’s theorem. Since
$T$
by Berger’s theorem. Since
![]() $M^{T}$
is a rational sphere, either
$M^{T}$
is a rational sphere, either
![]() $M^{g}$
is connected or it has two components and the
$M^{g}$
is connected or it has two components and the
![]() $T$
-actions on them have exactly one fixed point each. The latter case can only occur if each component of
$T$
-actions on them have exactly one fixed point each. The latter case can only occur if each component of
![]() $M^{g}$
is non-orientable (see again Bredon [Reference BredonBre72, Corollary IV.2.3, p. 178]), which in turn can only occur if
$M^{g}$
is non-orientable (see again Bredon [Reference BredonBre72, Corollary IV.2.3, p. 178]), which in turn can only occur if
![]() $g^{2}=\text{id}$
.◻
$g^{2}=\text{id}$
.◻
3 Proof of Corollary C
Corollary C is an easy consequence of Theorem A together with a few general classification results. We only use Theorem A to deduce that
![]() $\unicode[STIX]{x1D712}(M)=2$
.
$\unicode[STIX]{x1D712}(M)=2$
.
First, it is immediate that, if
![]() $M$
has vanishing odd-dimensional rational homology, then
$M$
has vanishing odd-dimensional rational homology, then
![]() $M$
is a rational homology sphere. Since
$M$
is a rational homology sphere. Since
![]() $M$
is simply connected, this is equivalent to
$M$
is simply connected, this is equivalent to
![]() $M$
having the rational homotopy type of a sphere. In particular, this case applies if
$M$
having the rational homotopy type of a sphere. In particular, this case applies if
![]() $M$
is rationally elliptic (see [Reference Félix, Halperin and ThomasFHT01, Proposition 32.10]) or if the action is equivariantly formal, that is, if the Leray–Serre spectral sequence of the Borel construction degenerates at the
$M$
is rationally elliptic (see [Reference Félix, Halperin and ThomasFHT01, Proposition 32.10]) or if the action is equivariantly formal, that is, if the Leray–Serre spectral sequence of the Borel construction degenerates at the
![]() $E_{2}$
-term (see [Reference Allday and PuppeAP93, Corollary 3.1.15]).
$E_{2}$
-term (see [Reference Allday and PuppeAP93, Corollary 3.1.15]).
Second, we refer to Powell [Reference PowellPow97] for a definition of
![]() $p$
-elliptic for a prime
$p$
-elliptic for a prime
![]() $p$
. In particular, it follows that
$p$
. In particular, it follows that
![]() $M$
is rationally elliptic and hence a rational sphere. In [Reference PowellPow97, Theorem 1], Powell classified
$M$
is rationally elliptic and hence a rational sphere. In [Reference PowellPow97, Theorem 1], Powell classified
![]() $p$
-elliptic rational spheres for
$p$
-elliptic rational spheres for
![]() $p\geqslant \dim (M)$
, and it follows immediately that
$p\geqslant \dim (M)$
, and it follows immediately that
![]() $M$
is a mod
$M$
is a mod
![]() $p$
homology sphere.
$p$
homology sphere.
Third, if
![]() $M$
has vanishing odd-dimensional integral homology, then its homology is torsion-free. Since
$M$
has vanishing odd-dimensional integral homology, then its homology is torsion-free. Since
![]() $M$
is a rational homology sphere,
$M$
is a rational homology sphere,
![]() $M$
is, in fact, an integral homology sphere. Since
$M$
is, in fact, an integral homology sphere. Since
![]() $M$
is simply connected, it follows from the resolution of the Poincaré conjecture that
$M$
is simply connected, it follows from the resolution of the Poincaré conjecture that
![]() $M$
is homeomorphic to a sphere.
$M$
is homeomorphic to a sphere.
Fourth, since biquotients are rationally elliptic,
![]() $M$
is again a rational sphere. Totaro [Reference TotaroTot02, Theorem 6.1] and Kapovitch and Ziller [Reference Kapovitch and ZillerKZ04, Theorem A] classified such biquotients, and their results immediately imply that
$M$
is again a rational sphere. Totaro [Reference TotaroTot02, Theorem 6.1] and Kapovitch and Ziller [Reference Kapovitch and ZillerKZ04, Theorem A] classified such biquotients, and their results immediately imply that
![]() $M$
is diffeomorphic to
$M$
is diffeomorphic to
![]() $\mathbb{S}^{2n}$
.
$\mathbb{S}^{2n}$
.
Fifth, if
![]() $M$
admits a cohomogeneity-one structure, it is rationally elliptic by Grove and Halperin [Reference Grove and HalperinGH87], hence
$M$
admits a cohomogeneity-one structure, it is rationally elliptic by Grove and Halperin [Reference Grove and HalperinGH87], hence
![]() $M$
is a rational sphere. Since
$M$
is a rational sphere. Since
![]() $M$
has no
$M$
has no
![]() $2$
-torsion in its homology, it follows that
$2$
-torsion in its homology, it follows that
![]() $M$
is a mod
$M$
is a mod
![]() $2$
homology sphere. The result now follows from Asoh’s classification up to equivariant diffeomorphism of mod
$2$
homology sphere. The result now follows from Asoh’s classification up to equivariant diffeomorphism of mod
![]() $2$
homology spheres that admit a cohomogeneity-one action (see [Reference AsohAso81, Main Theorem]).
$2$
homology spheres that admit a cohomogeneity-one action (see [Reference AsohAso81, Main Theorem]).
Finally, if
![]() $M$
is a simply connected, compact symmetric space, then it factors as
$M$
is a simply connected, compact symmetric space, then it factors as
![]() $M_{1}\times \cdots \times M_{k}$
for some irreducible symmetric spaces
$M_{1}\times \cdots \times M_{k}$
for some irreducible symmetric spaces
![]() $M_{i}$
. Since
$M_{i}$
. Since
![]() $\unicode[STIX]{x1D712}(M)>0$
, it follows that each
$\unicode[STIX]{x1D712}(M)>0$
, it follows that each
![]() $\unicode[STIX]{x1D712}(M_{i})\geqslant 2$
, with equality only if
$\unicode[STIX]{x1D712}(M_{i})\geqslant 2$
, with equality only if
![]() $M_{i}$
is a sphere. By Theorem A,
$M_{i}$
is a sphere. By Theorem A,
![]() $k=1$
and
$k=1$
and
![]() $M=M_{1}$
is a sphere.
$M=M_{1}$
is a sphere.
4 A simplified proof of a Betti number estimate
Fix
![]() $n\geqslant 4$
. Consider a closed, simply connected, even-dimensional Riemannian manifold
$n\geqslant 4$
. Consider a closed, simply connected, even-dimensional Riemannian manifold
![]() $M^{n}$
with positive sectional curvature. If
$M^{n}$
with positive sectional curvature. If
![]() $M$
admits an isometric action by a torus
$M$
admits an isometric action by a torus
![]() $T$
with
$T$
with
![]() $r=\dim (T)\geqslant 2\log _{2}(n)+1$
, the second author showed that the Betti numbers of
$r=\dim (T)\geqslant 2\log _{2}(n)+1$
, the second author showed that the Betti numbers of
![]() $M$
satisfy
$M$
satisfy
![]() $b_{2}(M)\leqslant b_{4}(M)\leqslant 1$
(see [Reference KennardKen14]). In this section, we provide a simplified and self-contained proof of this conclusion under the assumption that
$b_{2}(M)\leqslant b_{4}(M)\leqslant 1$
(see [Reference KennardKen14]). In this section, we provide a simplified and self-contained proof of this conclusion under the assumption that
![]() $r>\log _{4/3}(n-3)$
.
$r>\log _{4/3}(n-3)$
.
First, if
![]() $n=4$
, the bound on
$n=4$
, the bound on
![]() $r$
implies
$r$
implies
![]() $r\geqslant 1$
, so the Hsiang–Kleiner result implies
$r\geqslant 1$
, so the Hsiang–Kleiner result implies
![]() $b_{2}(M)\leqslant b_{4}(M)=1$
. If
$b_{2}(M)\leqslant b_{4}(M)=1$
. If
![]() $6\leqslant n\leqslant 22$
, the bound on
$6\leqslant n\leqslant 22$
, the bound on
![]() $r$
implies
$r$
implies
![]() $r\geqslant n/2$
, so the diffeomorphism classification of Grove and Searle implies
$r\geqslant n/2$
, so the diffeomorphism classification of Grove and Searle implies
![]() $b_{2}(M)=b_{4}(M)\leqslant 1$
(see [Reference Grove and SearleGS94]). We proceed by induction on the dimension
$b_{2}(M)=b_{4}(M)\leqslant 1$
(see [Reference Grove and SearleGS94]). We proceed by induction on the dimension
![]() $n$
to prove the result in general. Note that, if
$n$
to prove the result in general. Note that, if
![]() $M$
has
$M$
has
![]() $4$
-periodic rational cohomology, then
$4$
-periodic rational cohomology, then
![]() $b_{2}(M)\leqslant b_{4}(M)\leqslant 1$
by Poincaré duality. Indeed, the subring of
$b_{2}(M)\leqslant b_{4}(M)\leqslant 1$
by Poincaré duality. Indeed, the subring of
![]() $H^{\ast }(M;\mathbb{Q})$
made up of elements of even degree is isomorphic to that of
$H^{\ast }(M;\mathbb{Q})$
made up of elements of even degree is isomorphic to that of
![]() $\mathbb{S}^{n}$
,
$\mathbb{S}^{n}$
,
![]() $\mathbb{C}\mathbb{P}^{n/2}$
,
$\mathbb{C}\mathbb{P}^{n/2}$
,
![]() $\mathbb{H}\mathbb{P}^{n/4}$
or
$\mathbb{H}\mathbb{P}^{n/4}$
or
![]() $\mathbb{S}^{2}\times \mathbb{H}\mathbb{P}^{(n-2)/4}$
. (See, for example, the proofs of Wilking [Reference WilkingWil03, Propositions 7.3 and 7.4].) We may suppose that
$\mathbb{S}^{2}\times \mathbb{H}\mathbb{P}^{(n-2)/4}$
. (See, for example, the proofs of Wilking [Reference WilkingWil03, Propositions 7.3 and 7.4].) We may suppose that
![]() $M$
is not rationally
$M$
is not rationally
![]() $4$
-periodic.
$4$
-periodic.
By the Berger theorem, there is a fixed point
![]() $x\in M$
of the torus action. Take
$x\in M$
of the torus action. Take
![]() $y=x$
in Proposition 1.1, and choose an involution
$y=x$
in Proposition 1.1, and choose an involution
![]() $\unicode[STIX]{x1D704}\in T$
and a component
$\unicode[STIX]{x1D704}\in T$
and a component
![]() $N\subseteq M^{\unicode[STIX]{x1D704}}$
such that
$N\subseteq M^{\unicode[STIX]{x1D704}}$
such that
![]() $\dim \ker (T|_{N})\leqslant 1$
and
$\dim \ker (T|_{N})\leqslant 1$
and
![]() $(n-4)/4<\operatorname{cod}(N)\leqslant (n-4)/2$
. Note that
$(n-4)/4<\operatorname{cod}(N)\leqslant (n-4)/2$
. Note that
![]() $N$
is a closed, totally geodesic submanifold of even codimension. Also note that
$N$
is a closed, totally geodesic submanifold of even codimension. Also note that
![]() $N$
is simply connected by the connectedness lemma. The
$N$
is simply connected by the connectedness lemma. The
![]() $T$
-action restricts to
$T$
-action restricts to
![]() $N$
, and
$N$
, and
![]() $T/\text{ker}(T|_{N})$
is another torus that acts effectively on
$T/\text{ker}(T|_{N})$
is another torus that acts effectively on
![]() $N$
. Since the dimension of this torus is at least
$N$
. Since the dimension of this torus is at least
the induction hypothesis implies that
![]() $b_{2}(N)\leqslant b_{4}(N)\leqslant 1$
. By the connectedness lemma again, the inclusion
$b_{2}(N)\leqslant b_{4}(N)\leqslant 1$
. By the connectedness lemma again, the inclusion
![]() $N\rightarrow M$
is 5-connected, so the Betti numbers of
$N\rightarrow M$
is 5-connected, so the Betti numbers of
![]() $M$
satisfy the same bounds.
$M$
satisfy the same bounds.
Acknowledgements
We would like to thank B. Wilking for a motivating discussion on calculating Euler characteristics of positively curved manifolds with symmetry. We are also grateful to W. Ziller for alerting us to Asoh’s paper. The first author was supported by a research grant of the German Research Foundation. The second author was supported by National Science Foundation grants DMS-1045292 and DMS-1404670.