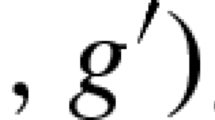Abstract
We consider the classical N. Steenrod’s problem of realization of cycles by continuous images of manifolds. Our goal is to find a class \( \mathcal{M}_n \) of oriented n-dimensional closed smooth manifolds such that each integral homology class can be realized with some multiplicity by an image of a manifold from the class \( \mathcal{M}_n \). We prove that as the class \( \mathcal{M}_n \) one can take a set of finite-fold coverings of the manifold M n of isospectral symmetric tridiagonal real (n + 1) × (n + 1) matrices. It is well known that the manifold M n is aspherical, its fundamental group is torsion-free, and its universal covering is diffeomorphic to ℝn. Thus, every integral homology class of an arcwise connected space can be realized with some multiplicity by an image of an aspherical manifold with a torsion-free fundamental group. In particular, for any closed oriented manifold Q n, there exists an aspherical manifold that has torsion-free fundamental group and can be mapped onto Q n with nonzero degree.
Similar content being viewed by others
References
N. Bourbaki, Éléments de mathématique, Fasc. 34: Groupes et algèbres de Lie, Chapitres IV, V et VI (Hermann, Paris, 1968; Mir, Moscow, 1972).
V. M. Buchstaber, “Modules of Differentials of the Atiyah-Hirzebruch Spectral Sequence. I, II,” Mat. Sb. 78(2), 307–320 (1969) [Math. USSR, Sb. 7, 299–313 (1969)]; Mat. Sb. 83 (1), 61–76 (1970) [Math. USSR, Sb. 12, 59–75 (1970)].
V. M. Buchstaber and T. E. Panov, Torus Actions in Topology and Combinatorics (MTsNMO, Moscow, 2004) [in Russian].
E. B. Vinberg, “Discrete Linear Groups Generated by Reflections,” Izv. Akad. Nauk SSSR, Ser. Mat. 35(5), 1072–1112 (1971) [Math. USSR, Izv. 5, 1083–1119 (1971)].
A. A. Gaifullin, “Local Formulae for Combinatorial Pontryagin Classes,” Izv. Ross. Akad. Nauk, Ser. Mat. 68(5), 13–66 (2004) [Izv. Math. 68, 861–910 (2004)].
A. A. Gaifullin, “Explicit Construction of Manifolds Realising Prescribed Homology Classes,” Usp. Mat. Nauk 62(6), 167–168 (2007) [Russ. Math. Surv. 62, 1199–1201 (2007)].
A. A. Gaifullin, “Realisation of Cycles by Aspherical Manifolds,” Usp. Mat. Nauk 63(3), 157–158 (2008) [Russ. Math. Surv. 63, 562–564 (2008)].
S. P. Novikov, “Homotopic Properties of Thom Complexes,” Mat. Sb. 57(4), 407–442 (1962).
R. Thom, “Quelques propriétés globales des variétés différentiables,” Comment. Math. Helv. 28, 17–86 (1954).
M. W. Davis, “Groups Generated by Reflections and Aspherical Manifolds not Covered by Euclidean Space,” Ann. Math., Ser. 2, 117(2), 293–324 (1983).
M. W. Davis, “Some Aspherical Manifolds,” Duke Math. J. 55(1), 105–139 (1987).
M. W. Davis and T. Januszkiewicz, “Convex Polytopes, Coxeter Orbifolds and Torus Actions,” Duke Math. J. 62(2), 417–451 (1991).
S. Eilenberg, “On the Problems of Topology,” Ann. Math., Ser. 2, 50, 247–260 (1949).
M. Ferri, “Una rappresentazione delle n-varietà topologiche triangolabili mediante grafi (n + 1)-colorati,” Boll. Unione Mat. Ital. B, Ser. 5, 13(1), 250–260 (1976).
M. Ferri, C. Gagliardi, and L. Grasselli, “A Graph-Theoretical Representation of PL-Manifolds—a Survey on Crystallizations,” Aequationes Math. 31(2–3), 121–141 (1986).
M. Pezzana, “Diagrammi di Heegaard e triangolazione contratta,” Boll. Unione Mat. Ital., Ser. 4, 12,Suppl. (3), 98–105 (1975).
D. Sullivan, “Singularities in Spaces,” in Proc. Liverpool Singularities Symposium II (Springer, Berlin, 1971), Lect. Notes Math. 209, pp. 196–206.
C. Tomei, “The Topology of Isospectral Manifolds of Tridiagonal Matrices,” Duke Math. J. 51(4), 981–996 (1984).
G. M. Ziegler, Lectures on Polytopes (Springer, Berlin, 1995), Grad. Texts Math. 152.
Author information
Authors and Affiliations
Additional information
Original Russian Text © A.A. Gaifullin, 2008, published in Trudy Matematicheskogo Instituta imeni V.A. Steklova, 2008, Vol. 263, pp. 44–63.
Rights and permissions
About this article
Cite this article
Gaifullin, A.A. The manifold of isospectral symmetric tridiagonal matrices and realization of cycles by aspherical manifolds. Proc. Steklov Inst. Math. 263, 38–56 (2008). https://doi.org/10.1134/S0081543808040044
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1134/S0081543808040044