Hostname: page-component-8448b6f56d-c4f8m Total loading time: 0 Render date: 2024-04-25T01:24:52.526Z Has data issue: false hasContentIssue false
  • English
  • Français

On stochastic recursive equations of sum and max type

Part of: Distribution theory - Probability Stochastic analysis Algorithms - Computer Science

Published online by Cambridge University Press:  14 July 2016

Ludger Rüschendorf
Ludger Rüschendorf*
Affiliation:
Albert-Ludwigs-Universität Freiburg
*
∗Postal address: Mathematisches Institut, Albert-Ludwigs-Universität Freiburg, Eckerstr. 1, 79104 Freiburg, Germany. Email address: ruschen@stochastik.uni-freiburg.de
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper we consider stochastic recursive equations of sum type, 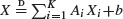, and of max type, 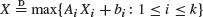, where Ai, bi, and b are random, (Xi) are independent, identically distributed copies of X, and 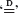denotes equality in distribution. Equations of these types typically characterize limits in the probabilistic analysis of algorithms, in combinatorial optimization problems, and in many other problems having a recursive structure. We develop some new contraction properties of minimal Ls-metrics which allow us to establish general existence and uniqueness results for solutions without imposing any moment conditions. As an application we obtain a one-to-one relationship between the set of solutions to the homogeneous equation and the set of solutions to the inhomogeneous equation, for sum- and max-type equations. We also give a stochastic interpretation of a recent transfer principle of Rösler from nonnegative solutions of sum type to those of max type, by means of random scaled Weibull distributions.

Keywords

Additive recursive equationrecursive algorithmcontraction method

MSC classification

Primary: 60E05: Distributions 68W40: Analysis of algorithms
Secondary: 60H30: Applications of stochastic analysis (to PDE, etc.)
Type
Research Article
Information
Journal of Applied Probability , Volume 43 , Issue 3 , September 2006 , pp. 687 - 703
Copyright
© Applied Probability Trust 2006 

References

Aldous, D. J. and Bandyopadhyay, A. (2005). “A survey of max-type recursive distributional equations. Ann. Appl. Prob. 15, 1047–1110.Google Scholar
Alsmeyer, G. and Rösler, U. (2003). “The best constant in the Topchii–Vatutin inequality for martingales.” Statist. Prob. Lett. 65, 199–206.Google Scholar
Biggins, J. D. (1977). “Martingale convergence in the branching random walk.” J. Appl. Prob. 14, 25–37.Google Scholar
Biggins, J. D. and Kyprianou, A. E. (1997). “Seneta–Heyde norming in the branching random walk.” Ann. Prob. 25, 337–360.Google Scholar
Caliebe, A. and Rösler, U. (2003). “Fixed points with finite variance of a smoothing transformation.” Stoch. Process. Appl. 107, 105–129.Google Scholar
Cramer, M. and Rüschendorf, L. (1996). “Convergence of a branching type recursion.” Ann. Inst. H. Poincaré Prob. Statist. 32, 725–741.Google Scholar
Devroye, L. (2001). “On the probabilistic worst-case time of ‘FIND’.” Algorithmica 31, 291–303.Google Scholar
Durrett, R. and Liggett, T. M. (1983). “Fixed points of the smoothing transformation.” Z. Wahrscheinlichkeitsth. 64, 275–301.Google Scholar
Fill, J. A. and Janson, S. (2000). “A characterization of the set of fixed points of the Quicksort transformation.” Electron. Commun. Prob. 5, 77–84.Google Scholar
Grübel, R. and Rösler, U. (1996). “Asymptotic distribution theory for Hoare's selection algorithm.” Adv. Appl. Prob. 28, 252–269.Google Scholar
Guivarc'h, Y. (1990). “Sur une extension de la notion de loi semi-stable.” Ann. Inst. H. Poincaré Prob. Statist. 26, 261–285.Google Scholar
Holley, R. and Liggett, T. M. (1981). “Generalized potlatch and smoothing processes.” Z. Wahrscheinlichkeitsth. 55, 165–195.Google Scholar
Hutchinson, J. E. and Rüschendorf, L. (1998). “Random fractal measures via the contraction method.” Indiana Univ. Math. J. 47, 471–487.Google Scholar
Hutchinson, J. E. and Rüschendorf, L. (2000). “Random fractals and probability metrics.” Adv. Appl. Prob. 32, 925–947.Google Scholar
Hutchinson, J. E. and Rüschendorf, L. (2000). “Selfsimilar fractals and selfsimilar random fractals.” In Fractal Geometry and Stochastics II, eds Brandt, C. et al., Birkhäuser, Basel, pp. 109–124.Google Scholar
Jagers, P. and Rösler, U. (2004). “Stochastic fixed point for the maximum.” In Mathematics and Computer Science III, eds Drmota, M. et al., Birkhäuser, Basel, pp. 165–195.Google Scholar
Liu, Q. (1998). “Fixed points of a generalized smoothing transformation and applications to the branching random walk.” Adv. Appl. Prob. 30, 85–112.Google Scholar
Lyons, R., Pemantle, R. and Peres, Y. (1995). “Conceptual proofs of Llog L criteria for mean behavior of branching processes.” Ann. Prob. 23, 1125–1138.Google Scholar
Neininger, R. and Rüschendorf, L. (2004). “A general limit theorem for recursive algorithms and combinatorial structures.” Ann. Appl. Prob. 14, 378–418.Google Scholar
Neininger, R. and Rüschendorf, L. (2004). “On the contraction method with degenerate limit equation.” Ann. Prob. 32, 2838–2856.Google Scholar
Neininger, R. and Rüschendorf, L. (2005). “Analysis of algorithms by the contraction method: additive and max-recursive sequences.” In Interacting Stochastic Systems, eds Deuschel, J.-D. and Greven, A., Springer, Berlin, 435–450.Google Scholar
Rachev, S. T. (1991).” Probability Metrics and the Stability of Stochastic Models. John Wiley, Chichester.Google Scholar
Rachev, S. T. and Rüschendorf, L. (1992). “Rate of convergence for sums and maxima and doubly ideal metrics.” Theory Prob. Appl. 37, 222–235.Google Scholar
Rachev, S. T. and Rüschendorf, L. (1995). “Probability metrics and recursive algorithms.” Adv. Appl. Prob. 27, 770–799.Google Scholar
Rösler, U. (1991). “A limit theorem for ‘Quicksort’.” RAIRO Inf. Théoret. Appl. 25, 85–100.Google Scholar
Rösler, U. (1992). “A fixed point theorem for distributions.” Stoch. Process. Appl. 42, 195–214.Google Scholar
Rösler, U. (2001). “On the analysis of stochastic divide and conquer algorithms.” Algorithmica 29, 238–261.Google Scholar
Rösler, U. (2003). “Notes on fixed points of max recursive sequences.” Preprint.Google Scholar
Rösler, U. and Rüschendorf, L. (2001). “The contraction method for recursive algorithms.” Algorithmica 29, 3–33.Google Scholar
Vatutin, V. A. and Topchiĭ, V. A.} (1997). “The maximum of critical Galton–Watson processes, and left-continuous random walks.” Theory Prob. Appl. 42, 17–27.Google Scholar