Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Brilman, Matthieu
and
Vincent, Jean-Marc
1998.
On the Estimation of the Throughput for a Class of Stochastic Resources Sharing Systems.
Mathematics of Operations Research,
Vol. 23,
Issue. 2,
p.
305.
Baccelli, François
and
Hong, Dohy
2000.
Analytic expansions of max-plus Lyapunov exponents.
The Annals of Applied Probability,
Vol. 10,
Issue. 3,
Baccelli, François
and
Hong, Dohy
2000.
Analyticity of iterates of random non-expansive maps.
Advances in Applied Probability,
Vol. 32,
Issue. 1,
p.
193.
Toomey, Fergal
2002.
Large Deviations of Products of Random Topical Operators.
The Annals of Applied Probability,
Vol. 12,
Issue. 1,
Gaujal, Bruno
Haar, Stefan
and
Mairesse, Jean
2003.
Blocking a transition in a free choice net and what it tells about its throughput.
Journal of Computer and System Sciences,
Vol. 66,
Issue. 3,
p.
515.
Huang, Jianyi
Kontoyiannis, Ioannis
and
Meyn, Sean P.
2006.
Stochastic Theory and Control.
Vol. 280,
Issue. ,
p.
205.
2006.
Max-Plus Linear Stochastic Systems and Perturbation Analysis.
Vol. 16,
Issue. ,
p.
179.
Van Der Woude, Jacob
and
Heidergott, Bernd
2006.
Asymptotic growth rate of stochastic max-plus systems that with a positive probability have a sunflower-like support.
p.
451.
KELLERER, HANS G.
and
WINKLER, G.
2006.
RANDOM DYNAMICAL SYSTEMS ON ORDERED TOPOLOGICAL SPACES.
Stochastics and Dynamics,
Vol. 06,
Issue. 03,
p.
255.
Merlet, Glenn
2007.
A central limit theorem for stochastic recursive sequences of topical operators.
The Annals of Applied Probability,
Vol. 17,
Issue. 4,
Bouillard, Anne
and
Gaujal, Bruno
2008.
Backward Coupling in Bounded Free-Choice Nets Under Markovian and Non-Markovian Assumptions.
Discrete Event Dynamic Systems,
Vol. 18,
Issue. 4,
p.
473.
Merlet, Glenn
2008.
Cycle time of stochastic max-plus linear systems..
Electronic Journal of Probability,
Vol. 13,
Issue. none,
Merlet, Glenn
2010.
Semigroup of matrices acting on the max-plus projective space.
Linear Algebra and its Applications,
Vol. 432,
Issue. 8,
p.
1923.
Merlet, Glenn
2010.
Memory Loss Property for Products of Random Matrices in the Max-Plus Algebra.
Mathematics of Operations Research,
Vol. 35,
Issue. 1,
p.
160.
Merlet, G.
2010.
Asymptotic throughput of stochastic max-plus linear systems..
IFAC Proceedings Volumes,
Vol. 43,
Issue. 12,
p.
388.
Goverde, Rob M.P.
Heidergott, Bernd
and
Merlet, Glenn
2011.
A coupling approach to estimating the Lyapunov exponent of stochastic max-plus linear systems.
European Journal of Operational Research,
Vol. 210,
Issue. 2,
p.
249.
Brackley, Chris A.
Broomhead, David S.
Romano, M. Carmen
and
Thiel, Marco
2012.
A max-plus model of ribosome dynamics during mRNA translation.
Journal of Theoretical Biology,
Vol. 303,
Issue. ,
p.
128.
Hook, James
2013.
Critical Path Statistics of Max-Plus Linear Systems with Gaussian Noise.
Journal of Applied Probability,
Vol. 50,
Issue. 03,
p.
654.
Whitt, Ward
2015.
The Maximum Throughput on a Golf Course.
Production and Operations Management,
Vol. 24,
Issue. 5,
p.
685.
Gupta, Abhimanyu
Boom, Ton van den
Woude, Jacob van der
and
Schutter, Bart De
2020.
Framework for Studying Stability of Switching Max-Plus Linear Systems.
IFAC-PapersOnLine,
Vol. 53,
Issue. 4,
p.
68.
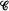 such that
such that 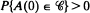 and the matrices
and the matrices 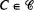 have a unique periodic regime.
have a unique periodic regime.



