Hostname: page-component-848d4c4894-2pzkn Total loading time: 0 Render date: 2024-05-09T04:24:09.468Z Has data issue: false hasContentIssue false
  • English
  • Français

Some formal relative consistency proofs

Published online by Cambridge University Press:  12 March 2014

Robert McNaughton
Get access Rights & Permissions [Opens in a new window]

Extract

These systems are roughly natural number theory in, respectively, nth order function calculus, for all positive integers n. Each of these systems is expressed in the notation of the theory of types, having variables with type subscripts from 1 to n. Variables of type 1 stand for natural numbers, variables of type 2 stand for classes of natural numbers, etc. Primitive atomic wff's (well-formed formulas) of Tn are those of number theory in variables of type 1, and of the following kind for n > 1: xi ϵ yi+1. Other wff's are formed by truth functions and quantifiers in the usual manner. Quantification theory holds for all the variables of Tn. Tn has the axioms Z1 to Z9, which are, respectively, the nine axioms and axiom schemata for the system Z (natural number theory) on p. 371 of [1]. These axioms and axiom schemata contain only variables of type 1, except for the schemata Z2 and Z9, which are as follows:

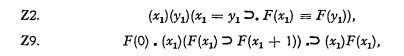
where ‘F(x1)’ can be any wff of Tn. Identity is primitive for variables of type 1; for variables of other types it is defined as follows:

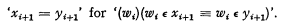
Type
Research Article
Information
The Journal of Symbolic Logic , Volume 18 , Issue 2 , June 1953 , pp. 136 - 144
Copyright
Copyright © Association for Symbolic Logic 1953

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

BIBLIOGRAPHY

[1]Hilbert, David and Bernays, Paul, Grand lagen der Mathematik, Berlin, 1934, vol. 1.Google Scholar
[2]Kemeny, John G., Type theory versus set theory, Dissertation, Princeton University, 1949.Google Scholar
[3]McNaughton, Robert, On establishing the consistency of systems, Dissertation, Harvard University, 1951.Google Scholar
[4]Mostowski, Andrzej, Some impredicative definitions in the axiomatic set theory, Fundamenta mathematical, vol. 37 (1950), pp. 111–124.CrossRefGoogle Scholar
[5]Novak, Ilse L., Doctoral Dissertation, Radcliffe College, 1948.Google Scholar
[6]Novak, Ilse L., A construction for models of consistent systems, Fundamenta mathematicae, vol. 37 (1950), pp. 87–110.CrossRefGoogle Scholar
[7]Quine, W. V., Mathematical logic, New York, 1940.Google Scholar
[8]Quine, W. V., Set theoretic foundations for logic, this Journal, vol. 1 (1936), pp. 45–57.Google Scholar
[9]Tarski, A., Der Wahrheitsbegriff in den formalisierten Sprachen, Studia philosophica, vol. 1 (1936), pp. 261–405.Google Scholar
[10]Wang, Hao, Arithmetic translations of axiom systems, Transactions of the American Mathematical Society, vol. 71 (1951), pp. 283–293.CrossRefGoogle Scholar
[11]Wang, Hao, On the consistency question of analysis, Cambridge, Mass., 1950 (mimeographed).Google Scholar
[12]Wang, Hao, Remarks on the comparison of axiom systems, Proceedings of the National Academy of Sciences, vol. 36 (1950), pp. 448–453.CrossRefGoogle ScholarPubMed
[13]Wang, Hao, Truth definitions and consistency proofs, Transactions of the American Mathematical Society, vol. 73 (1952), pp. 243–275.CrossRefGoogle Scholar
[14]Wang, Hao, A formal system of logic, this Journal, vol. 15 (1950), pp. 25–32.Google Scholar
[15]Quine, W. V., New foundations for mathematical logic, American mathematical monthly, vol. 44 (1937), pp. 70–80.CrossRefGoogle Scholar
[16]Wang, Hao, A theory of constructive types, Methodos (Milan), vol. 1 (1949), pp. 374–384.Google Scholar
[17]Rosser, J. B. and Wang, H., Non-standard models for formal logics, this Journal, vol. 15 (1950), pp. 113–129.Google Scholar