Let 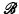be the collection of all sets which are finite Boolean combinations of recursively enumerable (r.e.) sets of numbers. Dale Myers asked [private correspondence] whether there exists a nonempty 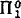class of sets containing no member of 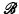. In this note we construct such a class. The motivation for Myers' question was his observation (reported in [1]) that the existence of such a class is equivalent to the assertion that there is a finite consistent set of tiles which has no m-trial tiling of the plane for any m (obeying the “origin constraint”). (For explanations of these terms and further results on tilings of the plane, cf. [1] and [5].) In addition to the application to tilings, the proof of our results gives some information on bi-immune sets and on complete extensions of first-order Peano arithmetic.

A 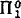class of sets may be roughly described as the class of infinite binary input tapes for which a fixed Turing machine fails to halt, or alternatively as the class of infinite branches of a recursive tree of finite binary sequences. (In these definitions, sets of numbers are identified with the corresponding binary sequences.) Precise definitions, as well as many results concerning such classes, may be found in [3] and [4].