Hostname: page-component-8448b6f56d-c4f8m Total loading time: 0 Render date: 2024-04-23T05:58:33.227Z Has data issue: false hasContentIssue false
  • English
  • Français

Analytic Sets, Baire Sets and the Standard Part Map

Published online by Cambridge University Press:  20 November 2018

C. Ward Henson
C. Ward Henson*
Affiliation:
University of Illinois at Urbana–Champaign, Urbana, Illinois
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The problems considered here arose in connection with the interesting use by Loeb [8] and Anderson [1], [2] of Loeb's measure construction [7] to define measures on certain topological spaces. The original problem, from which the results given here developed, was to identify precisely the family of sets on which these measures are defined.

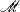To be precise, let be a set theoretical structure and * 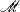a nonstandard extension of 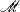, as in the usual framework for nonstandard analysis (see [10]). Let X be a Hausdorff space in 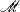and stx the standard part map for X, defined on the set of nearstandard points in *X. Suppose, for example, µ is an internal, finitely additive probability measure defined on the internal subsets of *X.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 31 , Issue 3 , 01 June 1979 , pp. 663 - 672
Copyright
Copyright © Canadian Mathematical Society 1979

References

1. Anderson, R. M., A non-standard representation for Brownian motion and Ito integration, Israel J. Math. 25 (1976), 15–46.Google Scholar
2. Anderson, R. M., Star-finite probability theory, Ph.D. Thesis, Yale University, 1977.Google Scholar
3. Bressler, D. W. and Sion, M., The current theory of analytic sets, Can. J. Math. 16 (1964), 207–230.Google Scholar
4. Comfort, W. W. and Negrepontis, S., Continuous pseudometrics, Marcel Dekker (New York, 1975).Google Scholar
5. Frolik, Z., A contribution to the descriptive theory of sets and spaces, General Topology and its Relations to Modern Analysis and Algebra, Proc. (1961) Prague Topological Symp. (Academic Press, New York, 1962), 157–173.Google Scholar
6. Henson, C. W., UnboundedLoeb measures, Proc. A.M.S., to appear.Google Scholar
7. Loeb, P., Conversion from nonstandard to standard measure spaces and applications in probability theory, Trans. Amer. Math. Soc. 211 (1975), 113–122.Google Scholar
8. Loeb, P., Applications of nonstandard analysis to ideal boundaries in potential theory, Israel J. Math. 25 (1976), 154–187.Google Scholar
9. Meyer, P. A., Probability and Potentials (Blaisdell Pub. Co., Waltham, Mass., 1966).Google Scholar
10. Stroyan, K. and Luxemburg, W. A. J., Introduction to the theory of infinitesimals (Academic Press, New York, 1976).Google Scholar