Hostname: page-component-76fb5796d-zzh7m Total loading time: 0 Render date: 2024-04-26T00:52:10.976Z Has data issue: false hasContentIssue false
  • English
  • Français

Perfect Sets of Uniqueness on the Group 2ω

Published online by Cambridge University Press:  20 November 2018

Kaoru Yoneda
Kaoru Yoneda*
Affiliation:
University of Osaka Prefecture, Sakai, Osaka, Japan
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let ω0, ω1, … denote the Walsh-Paley functions and let G denote the dyadic group introduced by Fine [3]. Recall that a subset E of G is said to be a set of uniqueness if the zero series is the only Walsh series ∑ akωk which satisfies

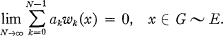
A subset E of G which is not a set of uniqueness is called a set of multiplicity.

It is known that any subset of G of positive Haar measure is a set of multiplicity [5] and that any countable subset of G is a set of uniqueness [2]. As far as uncountable subsets of Haar measure zero are concerned, both possibilities present themselves. Indeed, among perfect subsets of G of Haar measure zero there are sets of multiplicity [1] and there are sets of uniqueness [5].

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 34 , Issue 3 , 01 June 1982 , pp. 759 - 764
Copyright
Copyright © Canadian Mathematical Society 1982

References

1. Coury, J. E., A class of Walsh M-sets of measure zero, J. Appl. 31 (1970), 318-320, 52 (1975), 669–671.Google Scholar
2. Crittenden, R. B. and Shapiro, V. L., 5e/s of uniqueness on the group 2W, Ann. of Math. 81 (1965), 550–564.Google Scholar
3. Fine, N. J., On the Walsh functions, Trans. Amer. Math. Soc. 65 (1949), 372–414.Google Scholar
4. Salem, R., Sets of uniqueness and sets of multiplicity, Trans. Amer. Math. Soc. 54 (1943), 218-228, 56 (1944), 32–49.Google Scholar
5. Sneider, A. A., Uniqueness of expansions with respect to the Walsh system, Mat. Sbornik 24 (1949), 279–300.Google Scholar
6. Wade, W. R., Sets of uniqueness for the group of integers of a p-series field, Can. J. Math. 31 (1979), 858–866.Google Scholar
7. Zygmund, A., Trigonometric series (Cambridge University Press, 1959.Google Scholar