Hostname: page-component-8448b6f56d-c47g7 Total loading time: 0 Render date: 2024-04-17T18:08:32.243Z Has data issue: false hasContentIssue false
  • English
  • Français

Alternating 3-Forms and Exceptional Simple Lie Groups of Type G2

Published online by Cambridge University Press:  20 November 2018

Carl Herz
Carl Herz*
Affiliation:
McGill University, Montreal, Quebec
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

It is now customary to give concrete descriptions of the exceptional simple Lie groups of type G2 as groups of automorphisms of the Cayley algebras. There is, however, a more elementary description. Let W be a complex 7-dimensional vector space. Among the alternating 3-forms on W there is a connected dense open subset Ψ(W) of “maximal” forms. If ψ ∈ Ψ(W) then the subgroup of AUTC(W) consisting of the invertible complex-linear transformations S such that ψ(S•, S•, S•) = ψ(•, •, •) is denoted G(ψ), and, in Proposition 3.6. we prove

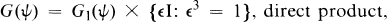
where G1(ψ) is identified with the exceptional simple complex Lie group of dimension 14. Thus the complex Lie algebra of type G2 is defined in terms of the alternating 3-form ψ alone without the need to specify an invariant quadratic form. In the real case the result is more striking.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 35 , Issue 5 , 01 October 1983 , pp. 776 - 806
Copyright
Copyright © Canadian Mathematical Society 1983

References

1. E., Cartan, Sur la structure des groupes simples finis et continus, C. R. Acad. Sci. Paris 116 (1893), p. 784–786 = Oeuvres complètes II (Gauthier-Villars, Paris 1952), 99-101.Google Scholar
2. E., Cartan, Sur la structure des groupes de transformations finis et continus, Thesis ( 1894) = Oeuvres complètes II, 137-287.Google Scholar
3. E., Cartan, Les groupes réels simples, finis et continus, Ann. Ecole Norm. Sup. Paris 31 (1914), 263–355 = Oeuvres complètes II, 399-491.Google Scholar
4. E., Cartan, Sur certaines formes riemanniennes remarquables des geometries à groupe fondamental simple, Ann. Ecole Norm. Sup. Paris 44 (1927), 345–467 = Oeuvres complètes 12, 867-988.Google Scholar
5. F., Engel, Sur un groupe simple à quatorze paramètres, C. R. Acad. Sci. Paris 116 (1893), 786–788.Google Scholar
6. S., Helgason, Differential geometry, Lie groups, and symmetric spaces (Academic Press, New York, 1978).Google Scholar
7. C., Herz, Symmetric spaces, (to appear).Google Scholar
8. R. D., Schafer, An introduction to nonassociative algebras (Academic Press, New York, 1966).Google Scholar
9. M., Zorn, The automorphisms of Cayley's non-associative algebra, Proc. Nat. Acad. Sci. U.S.A. 21 (1935), 355–358.Google Scholar