Hostname: page-component-76fb5796d-qxdb6 Total loading time: 0 Render date: 2024-04-25T23:26:54.221Z Has data issue: false hasContentIssue false
  • English
  • Français

Spherical Harmonics, the Weyl Transform and the Fourier Transform on the Heisenberg Group

Published online by Cambridge University Press:  20 November 2018

Daryl Geller
Daryl Geller*
Affiliation:
State University of New York at Stony Brook. Stony Brook, New York
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In the early days of quantum mechanics, Weyl asked the following question. Let λ be a non-zero real number, ℋa separable Hilbert space. Given certain (unbounded) operators W1,…,Wn,W1+, …, Wn+ on ℋ satisfying

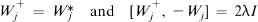
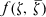(on a dense subspace D of ℋ) with all other commutators vanishing. Given also a function where ζ ∈ Cn. Let W = (W1 …, Wn) W+ = (W1+ …, Wn+). How does one associate to f an operator f(W, W+)? (Actually, Weyl phrased the question in terms of p = Re ζ, q = Im ζ, P = Re W, Q = Im W+ which represent momentum and position. In this paper, however, we wish to exploit the unitary group on Cn and so prefer complex notation.)

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 36 , Issue 4 , 01 August 1984 , pp. 615 - 684
Copyright
Copyright © Canadian Mathematical Society 1984

References

1. Bargmann, V., On a Hilbert space of analytic functions and an associated integral transform, Comm. Pure Appl. Math 14 (1961), 187–214.Google Scholar
2. Coifman, R. A., and Weiss, G., Representations of compact groups and spherical harmonics, L'Enseignement Mathématique 14 (1968), 121–172.Google Scholar
3. Erdelyi, A., et al., Higher transcendental functions, Vol. II (McGraw Hill, 1953).Google Scholar
4. Folland, G. B. and Stein, E. M., Estimates for the , complex and analysis on the Heisenherg group, Comm. Pure Appl. Math. 27 (1974), 429–522.Google Scholar
5. Gaveau, B., Principe de moindre action, propagation de la chaleur et estimées sous elliptiques sur certains groupes nilpotents. Acta Math. 139 (1977). 95–153.Google Scholar
6. Greller, D., Some results in Hp theory for the Heisenherg group, Duke Math J. 47 (1980), 365–390.Google Scholar
7. Greller, D., and Stein, E. M., Singular convolution operators on the Heisenherg group. Bull. Amer Math Soc. 6 (1982), 99–103.Google Scholar
8. Greller, D., Fourier analysis on the Heisenherg group I: Schwartz space, J. Func. Anal. 36 (1980). 205–254.Google Scholar
9. Greller, D., Local solvability and homogeneous distributions on the Ileisenherg group, Comm. in Partial Differential Equations 5 (1980), 475–560.Google Scholar
10. Greiner, P.C. and Stein, E. M., Estimates for the -Neumann problem (Princeton University Press. 1977).Google Scholar
11. Graham, R., The Dinchlet problem for the Bergman Laplacian, I and II. Comm. in Partial Differential Equations 8 (1983). 433–476 and 563–641.Google Scholar
12. Hirschmann, I. I. and Widder, D. V., The convolution transform (Princeton University Press, 1955).Google Scholar
13. Koranvi, A. and Yam, S., Singular integrals on homogeneous spaces and some problems of classical analysis, Ann. Scuola Norm Sup. Pisa 25 (1971). 575–648.Google Scholar
14. Miller, W., Lie theory and special junctions (Academic Press. 1968).Google Scholar
15. Peetre, J., The Weyl transform and Laguerre polynomials, Le Mathematiche Universita di calania Seminatio 27 (1972).Google Scholar
16. Stein, E. M., Boundary behavior of holomorphic functions of several complex variables (Princeton University Press, 1972).Google Scholar
17. Stein, E. M., An example on the Ileisenherg group related to the Lewy operator. Invent. Math. 69 (1982), 209–216.Google Scholar
18. Stein, E. M. and Weiss, G., Introduction to Fourier analysis on Euclidean spaces (Princeton University Press, 1971).Google Scholar
19. Vilenkin, N. Ja., Laguerre polynomials. Whittaker functions and representations of the group of bounded matrices, Mat. Sbornik 75 (1968), 432–444.Google Scholar