Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Deitmar, Anton
and
Hoffmann, Werner
1999.
On Limit Multiplicities for Spaces of Automorphic Forms.
Canadian Journal of Mathematics,
Vol. 51,
Issue. 5,
p.
952.
Levy, Jason
2001.
A Truncated Integral of the Poisson Summation Formula.
Canadian Journal of Mathematics,
Vol. 53,
Issue. 1,
p.
122.
Suzuki, M.
and
Weng, L.
2008.
Zeta Functions for G2 and Their Zeros.
International Mathematics Research Notices,
Hoffmann, Werner
2008.
Geometric estimates for the trace formula.
Annals of Global Analysis and Geometry,
Vol. 34,
Issue. 3,
p.
233.
Weng, Lin
2009.
Appendix: Zeta functions for Sp(2n).
Journal of Number Theory,
Vol. 129,
Issue. 3,
p.
567.
Lapid, Erez
and
Müller, Werner
2009.
Spectral asymptotics for arithmetic quotients of SL(n,R)/SO(n).
Duke Mathematical Journal,
Vol. 149,
Issue. 1,
Finis, Tobias
and
Lapid, Erez
2011.
On the continuity of Arthur’s trace formula: the semisimple terms.
Compositio Mathematica,
Vol. 147,
Issue. 3,
p.
784.
Feigon, Brooke
Lapid, Erez
and
Offen, Omer
2012.
On representations distinguished by unitary groups.
Publications mathématiques de l'IHÉS,
Vol. 115,
Issue. 1,
p.
185.
Matz, Jasmin
2015.
Bounds for global coefficients in the fine geometric expansion of Arthur’s trace formula for GL(n).
Israel Journal of Mathematics,
Vol. 205,
Issue. 1,
p.
337.
Finis, Tobias
Lapid, Erez
and
Müller, Werner
2015.
LIMIT MULTIPLICITIES FOR PRINCIPAL CONGRUENCE SUBGROUPS OF AND.
Journal of the Institute of Mathematics of Jussieu,
Vol. 14,
Issue. 3,
p.
589.
Ichino, Atsushi
and
Yamana, Shunsuke
2015.
Periods of automorphic forms: the case of .
Compositio Mathematica,
Vol. 151,
Issue. 4,
p.
665.
Matz, Jasmin
2016.
Families of Automorphic Forms and the Trace Formula.
p.
351.
Chaudouard, Pierre-Henri
and
Laumon, Gérard
2016.
SUR LE COMPTAGE DES FIBRÉS DE HITCHIN NILPOTENTS.
Journal of the Institute of Mathematics of Jussieu,
Vol. 15,
Issue. 1,
p.
91.
Müller, Werner
2016.
Families of Automorphic Forms and the Trace Formula.
p.
477.
Finis, Tobias
and
Lapid, Erez
2016.
On the Continuity of the Geometric Side of the Trace Formula.
Acta Mathematica Vietnamica,
Vol. 41,
Issue. 3,
p.
425.
Flicker, Yuval Z.
2016.
Arthur's Invariant Trace Formula and Comparison of Inner Forms.
p.
317.
Matz, Jasmin
and
Müller, Werner
2017.
Analytic torsion of arithmetic quotients of the symmetric space $${\rm SL} (n,\mathbb{R})/ {\rm SO}(n)$$ SL ( n , R ) / SO ( n ).
Geometric and Functional Analysis,
Vol. 27,
Issue. 6,
p.
1378.
Chaudouard, Pierre-Henri
2017.
Sur la contribution unipotente dans la formule des traces d’Arthur pour les groupes généraux linéaires.
Israel Journal of Mathematics,
Vol. 218,
Issue. 1,
p.
175.
Finis, Tobias
Hoffmann, Werner
and
Wakatsuki, Satoshi
2018.
Geometric Aspects of the Trace Formula.
p.
163.
Wakatsuki, Satoshi
2018.
The dimensions of spaces of Siegel cusp forms of general degree.
Advances in Mathematics,
Vol. 340,
Issue. ,
p.
1012.
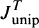 . We shall recall the precise definition in Section 1.
. We shall recall the precise definition in Section 1.



