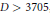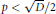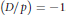Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Sándor, J.
and
Crstici, B.
2004.
Handbook of Number Theory II.
p.
179.
Sun, Zhi-Wei
2007.
Simple arguments on consecutive power residues.
Journal of Number Theory,
Vol. 124,
Issue. 1,
p.
57.
Adam, David
and
Cahen, Paul-Jean
2011.
Newtonian and Schinzel quadratic fields.
Journal of Pure and Applied Algebra,
Vol. 215,
Issue. 8,
p.
1902.
Adam, David
and
Cahen, Paul-Jean
2011.
Newton and Schinzel sequences in quadratic fields.
Actes des rencontres du CIRM,
Vol. 2,
Issue. 2,
p.
15.
McGown, Kevin
and
Treviño, Enrique
2021.
Mexican Mathematicians in the World.
Vol. 775,
Issue. ,
p.
205.