Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Cazzola, M.
and
Di Martino, L.
1993.
(2,3)-generation of PSp(4, q), q = p n, p ≠ 2,3.
Results in Mathematics,
Vol. 23,
Issue. 3-4,
p.
221.
Woldar, Andrew J.
1994.
3/2—Generation of the sporadic simple groups.
Communications in Algebra,
Vol. 22,
Issue. 2,
p.
675.
Martino, lino Di
and
Vavilov, Nikoli
1994.
(2,3)-Generation of SL(n,q).I. cases n=5,6,7.
Communications in Algebra,
Vol. 22,
Issue. 4,
p.
1321.
Sanchini, Paolo
and
Tamburini, M. Chiara
1994.
Constructive (2,3)-generation: A permutational approach.
Rendiconti del Seminario Matematico e Fisico di Milano,
Vol. 64,
Issue. 1,
p.
141.
Martino, Lino Di
and
Vavilov, Nikolai
1996.
(2,3)-Generation of sl(n,q). II. cases n ≥ 8.
Communications in Algebra,
Vol. 24,
Issue. 2,
p.
487.
Geck, Meinolf
Hiss, Gerhard
L�beck, Frank
Malle, Gunter
and
Pfeiffer, G�tz
1996.
CHEVIE ? A system for computing and processing generic character tables.
Applicable Algebra in Engineering, Communication and Computing,
Vol. 7,
Issue. 3,
p.
175.
Guralnick, Robert M.
Liebeck, Martin W.
Saxl, Jan
and
Shalev, Aner
1999.
Random Generation of Finite Simple Groups.
Journal of Algebra,
Vol. 219,
Issue. 1,
p.
345.
Di Martino, L.
Tamburini, M.C.
and
Zalesskii, A.E.
2000.
On hurwitz groups of low rank.
Communications in Algebra,
Vol. 28,
Issue. 11,
p.
5383.
Vsemirnov, Maxim
Mysovskikh, Vitaliy
and
Tamburini, M.Chiara
2001.
Triangle Groups as Subgroups of Unitary Groups.
Journal of Algebra,
Vol. 245,
Issue. 2,
p.
562.
Semenov, N. S.
2005.
Towards the Hurwitz Generation of Gsc(E6, q).
Journal of Mathematical Sciences,
Vol. 130,
Issue. 3,
p.
4768.
Plesken, W.
and
Robertz, D.
2006.
Representations, commutative algebra, and Hurwitz groups.
Journal of Algebra,
Vol. 300,
Issue. 1,
p.
223.
Tamburini, M.C.
and
Vsemirnov, M.
2006.
Vol. 4,
Issue. ,
p.
385.
Vincent, R.
and
Zalesski, A.E.
2007.
Non-Hurwitz Classical Groups.
LMS Journal of Computation and Mathematics,
Vol. 10,
Issue. ,
p.
21.
Tamburini, M. Chiara
and
Vsemirnov, M.A.
2009.
Irreducible (2,3,7)-subgroups of PGLn(F), n⩽7, II.
Journal of Algebra,
Vol. 321,
Issue. 8,
p.
2119.
Conder, Marston
2010.
An update on Hurwitz groups.
Groups – Complexity – Cryptology,
Vol. 2,
Issue. 1,
Marion, Claude
2010.
On triangle generation of finite groups of Lie type.
Journal of Group Theory,
Vol. 13,
Issue. 5,
Vsemirnov, M. A.
2011.
More classical groups which are not (2, 3)-generated.
Archiv der Mathematik,
Vol. 96,
Issue. 2,
p.
123.
Jones, Gareth A.
2012.
Hypermaps and multiply quasiplatonic Riemann surfaces.
European Journal of Combinatorics,
Vol. 33,
Issue. 7,
p.
1588.
Mushtaq, Qaiser
and
Rafiq, Ayesha
2013.
Adjacency Matrices of PSL(2,5) and Resemblance of Its Coset Diagrams with Fullerene C60.
Algebra Colloquium,
Vol. 20,
Issue. 04,
p.
541.
Garion, Shelly
2015.
Beauville Surfaces and Groups.
Vol. 123,
Issue. ,
p.
63.




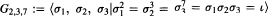 are called Hurwitz groups. Here we prove that apart from
are called Hurwitz groups. Here we prove that apart from 