
Invited Addresses, Sessions, and Other Activities
Below are some selected events from the wide variety of activities at the meeting:
- The Genome Project for Three-Manifolds - MAA Invited Address by Jeffrey Brock
- Statistics for Smart People Who Don't Know Anything About Statistics - AMS-MAA Invited Address by Persi Diaconis
- Automorphisms of Free Groups, Outer Space, and Beyond - AWM Emmy Noether Lecture by Karen Vogtmann
- Barcodes: The Persistent Topology of Data - Part of the AMS Current Events Bulletin, by Robert Ghrist
- Why "Mathematicians of the African Diaspora"? - NAM Cox-Talbot Address by Scott W. Williams
- Math Circles and Similar Programs for Students and Teachers - AMS-MAA Special Session
- Project NExT Events
- Mathematics and the Geometry of Voting - an MAA Minicourse organized by Donald Saari
- Using Origami in Undergraduate Math Classes - an MAA Minicourse organized by Thomas C. Hull
- The Aftermath of Katrina - a session organized by the AMS Committee on the Profession
- Students Flock to New Orleans
The Genome Project for Three-Manifolds - MAA Invited Address by Jeffrey Brock (Brown University)
It is now widely accepted within the mathematical community that the Poincaré Conjecture and Thurston's Geometrization Conjecture are no longer conjectures, but actual theorems, thanks to the seminal ideas of Richard Hamilton, which were recently taken to their ultimate conclusion by Grigory Perelman. The proof of these results settles questions that drove much of the research in three-manifold topology during the twentieth century. What's next for this field? Jeffrey Brock of Brown University explored this question in his MAA Invited Address. The proof of the Geometrization Conjecture established (loosely speaking) that all three-manifolds admit one of eight geometric structures. But the mere existence of these structures tells us nothing about the geometric properties of three-manifolds. If one thinks like a biologist, Brock proposed, one might ask, How does the topology of a three-manifold determine its geometry? Can one do "topological genomics" and create a taxonomy of three-manifolds? What kind of data could serve as the "DNA" of three-manifolds? Thurston showed that "most" three-manifolds admit a hyperbolic geometric structure, and Mostow rigidity shows that this structure is unique. But these results give no effective information about the nature of the hyperbolic structure on any given three-manifold. Work of Brock, Richard Canary, and Yair Minsky shows that the nature of a hyperbolic structure on a three-manifold is uniquely determined by its "end invariants" (end invariants are analogous to simple closed curves on surfaces). Brock called end invariants the DNA that determines the manifolds' geometric morphology. Brock also described similar efforts to use Heergaard splittings to produce geometric models for hyperbolic three-manifolds. Just as DNA is thought to provide a Rosetta Stone for the nature of living creatures, the work discussed in Brock's lecture might one day provide a Rosetta Stone for three-manifolds.
--- Allyn Jackson, Notices Senior Writer and Deputy Editor
Statistics for Smart People Who Don't Know Anything About Statistics - AMS-MAA Invited Address by Persi Diaconis (Stanford University)
| Diaconis delighted the packed house talking about statistics, and its strong connection to mathematics. He gave the framework of a typical probability problem and said that a typical statistics problem is the inverse of a probability problem. One particular problem he talked about in great detail was how in 1801 Gauss predicted where astronomers would find the asteroid Ceres. Telling this story gave Diaconis the opportunity to say things like, "Gauss assumed the error was Gaussian." Ceres had been discovered and followed for over a month but then astronomers lost it. Gauss, at the age of 24, analyzed error in the observations of Ceres, and by using a normal (Gaussian) distribution, he predicted where Ceres would be: "And the first clear night, when the planet [Ceres] was sought for as directed by the numbers deduced from it, restored the fugitive to observation." It was a triumphant moment for Gauss and mathematics, and showed the importance of statistics. Diaconis concluded his address with brief descriptions of how mathematical fields like algebraic topology, algebraic geometry, differential geometry, and respresentation theory are used in statistics. ---Mike Breen, AMS Public Awareness Officer |  |
Automorphisms of Free Groups, Outer Space, and Beyond - Association for Women in Mathematics Emmy Noether Lecture by Karen Vogtmann (Cornell University)
On a background of the night sky, Karen Vogtmann happily displayed a stunning picture of the non-astronomical Outer Space for n = 2 embedded in infinite projective space. This Outer Space is one on which Out(F2) acts in symmetric fashion, much as D6 acts on a six-pointed star. As motivation for studying automorphisms of free groups, connections were drawn between their actions on Outer Space, mapping class groups actions on Teichmuller Space, and arithmetic groups actions on homogeneous space. The homology of Out(Fn) has also shed light on symplectic Lie Algebras. In Vogtmann’s area of study, geometric group theory, groups are examined in tandem with the spaces on which they act. Geometric and topological information about the space provides insight into the structure of the group and visa versa.
Colorful diagrams illustrated the "spine" of outer space, a deformation retract with desirable properties. And a close-up of Outer Space showed a collection of graphs with labels, each associated with a simplex. One moves through the space by contracting edges and altering the labels to obtain nearby graphs. Detailed explanations with pictures are available in Vogtmann's survey paper of the same title as the talk at. This talk continued the 28-year-old tradition of honoring outstanding women mathematicians by inviting them to give an expository lecture.
--- Brie Finegold, 2006 AMS-AAAS Media Fellow
Barcodes: The Persistent Topology of Data - AMS Current Events Bulletin by Robert Ghrist (University of Illinois)
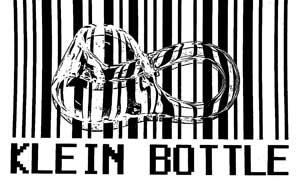 Image courtesy of Robert Ghrist | Data points often seem chaotic and unorganized. But with the right lens, one may see order and distinguishing characteristics. Homology, a tool of algebraic topology, is the lens used by Robert Ghrist and others to filter data and find persistent topological characteristics. One appeal of homology lies in its ease of computability compared to other topological invariants. By creating a parametrized family of simplicial complexes built from the original sampling of data points, Ghrist explained how one could construct a "bar code" giving a quick visual indication of the most prominent features of the data, sorted according to dimension. As an example, he showed a series of complexes built from a small sampling of points from a torus. The barcode for even this small sampling correctly indicated one or two "holes." |
For a more impressive example, data points from a large sample of grayscale digital pictures of natural imagery were combed through in hopes of finding natural patterns or structure. By selecting small 3x3 grids of pixels to analyze, persistent homology was revealed in three "loops" (generators of the first homology group) inside the resulting nine-dimensional space. These loops passed through data points in such a way as to suggest that nature exhibits a preference for certain visual arrangements. Furthermore the higher homology indicated a way to embed a Klein Bottle into the space of pixilated images, thus the picture of the Klein bottle atop a barcode. For pictures from this talk, and for text and images from the other three talks in the session, refer to the Current Events Bulletin booklet.
--- Brie Finegold, 2006 AMS-AAAS Media Fellow
Why “Mathematicians of the African Diaspora”? - National Association of Mathematicians Cox-Talbot Address by Scott W. Williams (University at Buffalo, SUNY)
Scott Williams spoke at the NAM banquet concerning his website Mathematicians of the African Diaspora (M.A.D.), hosted by SUNY Buffalo. Williams created the site in the 90’s, after years of struggling to find and maintain connections amongst mathematicians with African heritage. In one story, Dr. Williams told of his hiring at SUNY Buffalo, and how surprised he was to see in the headlines of the local paper that "one of the top three black mathematicians was hired." The other two were not mentioned, and he was not sure who they were supposed to be anyway.
In an effort to create a nationwide community of black mathematicians, M.A.D. provides information on upcoming conferences, listings of new Ph.D.’s and working mathematicians, and relevant statistics. Williams stressed the site’s role in inspiring black youth to look past typical stereotypes and view mathematics as a natural choice of study. During Black History Month, he receives thousands of emails and hits as students search for events such as the hiring of the first African-American mathematics professor (in 1849). Other links lead to biographies of mathematicians who succeeded despite racial prejudice, and excerpts from the ancient history of mathematics in Africa. Many audience members expressed an appreciation for the site and interest in continuing it in the future.
--- Brie Finegold, 2006 AMS-AAAS Media Fellow
Math Circles and Similar Programs for Students and Teachers - AMS-MAA Special Session
Math circles are informal get-togethers, often held on Saturdays, that provide a forum for schoolchildren to explore mathematics. Generally led by mathematicians, math circles emphasize play and discovery rather than the "cover the material" approach of most school mathematics classrooms. The wide variety of math circles now in existence in the United States was on display in this special session. One of the session organizers, Hugo Rossi of the Mathematical Sciences Research Institute (MSRI) in Berkeley, said that when MSRI began to get involved with math circles in 1997, there was only one, started in 1994 by Robert and Ellen Kaplan in Cambridge, Massachusetts. Rossi said that today MSRI knows of about 30 math circles in the United States.
Among the speakers at the special session were those two pioneers, the Kaplans, whose math circle nowadays has 10 teachers and around 120 students. They do no advertising; people hear about the circle through word of mouth. The Kaplans' approach dispenses entirely with competition: As Ellen Kaplan put it, they do not want a room full of kids with one winner and a bunch of losers. The Kaplans also want to break the "myth" that math is only for the talented, asserting that talent is no more needed for kids to do math than it is for kids to learn to read. As Ellen Kaplan put it, "Curiosity is passport enough to the republic of math."
Presentations by others who lead math circles show that not everyone hews to the Kaplan approach, with some circles making competition central to the way they operate. Inevitably, many math circles cater to elite kids---those whose parents, as session speaker Paul Zeitz of the University of San Francisco put it, spend their evenings surfing the web in search of enrichment activities for their kids. Zeitz launched the San Francisco Math Circle to reach those without such advantages. This circle has to operate rather differently from other circles; for example, it relies on teachers, rather than parents, to bring the students to circle meetings. The meetings take place after school, rather than on Saturdays, so there is not as much time as in other math circles. Nevertheless, within these constraints the San Francisco Math Circle has been successful in reaching many students who would otherwise never have this kind of exposure to mathematics.
--- Allyn Jackson, Notices Senior Writer and Deputy Editor
At the Joint Meetings Project NExT (New Experiences in Teaching) also conducted its own seminars. Project NExT is a program of the MAA for math faculty starting their first or second year of teaching. The program addresses all aspects of an academic career, including improving the teaching and learning of mathematics, engaging in research and scholarship, and participating in professional activities. It also provides the participants with a network of peers and mentors as they assume these responsibilities.
 | For the Joint Meetings the 2006-2007 class of Project NExT organized several sessions on a variety of topics, including: AP Exams; applying for research and education grants; balancing life, teaching and research; mentoring graduate students; assessment; course development; and several sessions pertaining to research after the Ph.D. In addition, Project NExT fellows from previous classes organized sessions, open to all at the Joint Meetings, around issues facing faculty with four to ten years of teaching experience. These topics included keeping research alive, becoming a leader in your department, publishing your first book, dealing with curriculum issues, and publishing undergraduate research and expository articles. All of these sessions included panels of invited speakers who gave their views and experiences on the issues at hand and also answered questions from those in attendance. (At left and below are pictures from the Young Mathematicians Network-Project NExT poster session.)
|
 |
Mathematics and the Geometry of Voting - an MAA Minicourse by Donald Saari (University of California, Irvine)
| Don Saari’s Minicourse shed the light of modern mathematics on some fundamental controversies over voting methods that have been debated in Western culture since the 18th century. Having collected all the votes for an election, different but seemingly fair tallying methods may lead to different winners. When Saari claimed that approval voting amongst the three major candidates in 1992 could have led to President Perot, he definitely had everyone’s attention. Using modern mathematics, different voting rules (e.g.- approval, plurality, positional) can be arranged and analyzed geometrically. For an election amongst three candidates, the space of possible rankings is six dimensional but can be represented by an equilateral triangle divided into six equal sections. As the speaker gave analogies between a basis for this six-dimensional space and the main ingredients in a good cup of coffee, the course provided material that was accessible to classroom teachers as well as research-worthy for working mathematicians. Saari ended by discussing his own research in which he recast Kenneth Arrow’s 1960’s conclusion. Arrow's research is often interpreted as meaning that no voting system is fair. Saari argues that is not a fair interpretation, and that by truly using all of the hypotheses in Arrow's Theorem, the Borda count emerges as the preferable voting method. The Borda count, named after an eighteenth century mathematician, gives top-ranked candidates two votes, second-ranked candidates one vote, and third-ranked no votes. |
Throughout the course, audience participation was high, and questions ranged from the philosophical "Is there such thing then as the will of the voters?" to the more mathematical "What is the significance of the eigenvalues of that matrix?" All questions were met with answers, stories, or enthusiastic encouragement to pursue research. Mathematicians’ collaborations with social scientists will undoubtedly increase in other areas, as it has in voting theory.
--- Brie Finegold, 2006 AMS-AAAS Media Fellow
Using Origami in Undergraduate Math Classes - an MAA Minicourse organized by Thomas C. Hull (Merrimack College)
 | As early as the 1800’s, origami and math were linked via geometric problems posted on Japanese temple walls. Not to be outdone by their 19th century counterparts, participants in this minicourse twisted, creased, and connected square pieces of paper, all without the aid of glue or conventional measuring devices. Using origami techniques, around twenty high school teachers, graduate students, and professors trisected the angle, created the illusion of a parabola using its tangent lines, and constructed polyhedra of all types. For "homework" everyone happily created an aesthetically pleasing model by fitting together as many as thirty smaller modular origami pieces together to form a whole. The models and their underlying geometric structure came into question as students noticed that the same module made a cube, a capped octahedron, and a capped icosahedron. A pattern was found by thinking of a cube as a tetrahedron capped by pyramids. |
--- Brie Finegold, 2006 AMS-AAAS Media Fellow The Aftermath of Katrina
Fifteen hundred people died in connection with Hurricane Katrina, which hit New Orleans in the fall of 2005, and 80 percent of the city's population was displaced. The Joint Meetings were held at a time when much of New Orleans was still recovering from the devastation. The JMM took place in two hotels in downtown New Orleans, next to the French Quarter, a part of the city that emerged largely unscathed in the hurricane. But some mathematicians ventured out to other areas that had been hard hit and returned with tales of eerily deserted neighborhoods devoid of any living creatures, where power lines were still down and reconstruction had not yet begun. The JMM included a session called "Katrina and Its Aftermath: Institutional Survival in New Orleans since the Storm," organized by Jim E. Hoste of Pitzer College and sponsored by the AMS Committee on the Profession, which Hoste chairs. The session brought together four speakers from area universities, who described how their institutions have fared. The speakers were Kenneth Holladay of the University of New Orleans, Morris Kalka of Tulane University, Vlajko L. Kocic of Xavier University of New Orleans, and Katarzyna Saxton of Loyola University New Orleans. Due to losses incurred during the storm, the universities underwent major reorganizations that brought large cuts in staff and the elimination of whole departments. As Holladay explained, the losses of the University of New Orleans were so great that it applied to the state government for an allowance to declare a state of financial exigency; the allowance was granted after the second application. The declaration of financial exigency permitted the university to eliminate tenure, paving the way for faculty to be fired. A combination of firings, early retirements, and voluntary departures has reduced the faculty by about 100 people. Because enrollments have fallen so sharply, these faculty are not being replaced. Although Loyola University had less damage and thus did not declare financial exigency, the university administration instituted a reorganization that entailed the firing of tenured faculty. In the turmoil that followed, the faculty of the College of Arts and Sciences took a vote of no confidence in the provost and president. Saxton said that the American Association of University Professors formed a special committee to investigate the treatment of faculty at universities in New Orleans, including Loyola and Tulane. Kalka spoke of huge financial losses at Tulane, which also underwent a painful restructuring that entailed large staff cuts and the elimination of departments and graduate programs. However, the Tulane mathematics department fared relatively well and was not cut in the restructuring. Xavier is a Catholic, historically black university, and it sustained enormous damage during the storm. Kocic reported that the mathematics department faculty fell from 16 pre-Katrina to 8 today. The size of the student body is 70 percent of what it was before the storm. Kocic said the mathematics department is struggling with a low number of students. "Katrina changed a lot of things, and we don't know where we are heading," he said. In the question period at the end of the session, there were complaints---in particular from Lee Lorch of York University and Abdulalim Shabazz of Lincoln University---that insufficient attention has been paid to the plight of mathematicians at historically black institutions in the areas hit by Katrina.
On a more optimistic note, the JMM held a raffle and T-shirt sale and raised a total of US$10,000 for a local relief charity. Individual mathematicians also showed generosity in making personal donations. One especially noteworthy example is Jennifer Quinn, executive director of the Association for Women in Mathematics, who received the MAA's Haimo Award for Distinguished College or University Teaching of Mathematics. The award came with a cash prize of US$1000, which Quinn donated to the New Orleans Area Habitat for Humanity.
--- Allyn Jackson, Notices Senior Writer and Deputy Editor
One factor in the large turnout (the largest ever, at over 5200 registrants) was a big surge in the number of students attending. AMS Director of Meetings Diane Saxe asked her staff to prepare statistics about the number of student attendees and found that there was a 33 percent increase between the Baltimore JMM in 2003 and the New Orleans JMM in 2007. In fact, students accounted for nearly a quarter of registrants in New Orleans. About half of the graduate students in New Orleans took part in the Employment Register. The strong attendance by undergraduates is likely due to the increasing number of these students involved in research. Darren Narayan, Carl Lutzer, Bernard Brooks, and Tamas Wiandt, all of the University of Rochester, together with Michael Fisher of California State University in Fresno, organized an AMS-MAA-SIAM special session that provided a venue for undergraduates to present their research. The organizers had so many takers that they requested and then filled an extra day for the session.
--- Allyn Jackson, Notices Senior Writer and Deputy Editor
 There were 166 presentations at the undergraduate poster session on Sunday afternoon |
 |  |
Puzzling at the Student Hospitality Center
|  Planning |



