
Invited Addresses, Sessions, and Other Activities
Below are summaries of some of the invited addresses and other sessions at the 2012 Joint Mathematics Meetings, almost all of which were written by Melanie DeVries, a graduate student at the University of Nebraska and 2011 AMS-AAAS Media Fellow, and Claudia Clark, freelance science writer and former AMS-AAAS Media Fellow. Also see the JMM2012 blog written by former AMS- AAAS Media Fellow Adriana Salerno of Bates College.
Slideshow of Invited Addresses and Other Sessions
AMS Retiring Presidential Address: Our Challenges, George Andrews (Penn State)
 AMS past-president George Andrews, who was president from 2009 to 2011, introduced his talk by referring to a letter with which most AMS members are familiar. The letter, written by National Science Foundation Division of Mathematical Sciences Director Dr. Sastry Pantula, contains a proposal to change the division’s name to the Division of Mathematical and Statistical Sciences. In the letter, Pantula refers to "one aspect of the information technology revolution"—-the "data deluge"—-and the increasing importance of data-intensive research, which he says will "drive many of the major scientific breakthroughs in the coming decades." (In fact, the NSF has recently created a new program, Computational and Data-Enabled Science and Engineering (CDS&E), which is described on their website as "a critical third pillar" of science—-theory and experimentation being the first two—-that is "revolutionizing the way science and engineering are done.")
AMS past-president George Andrews, who was president from 2009 to 2011, introduced his talk by referring to a letter with which most AMS members are familiar. The letter, written by National Science Foundation Division of Mathematical Sciences Director Dr. Sastry Pantula, contains a proposal to change the division’s name to the Division of Mathematical and Statistical Sciences. In the letter, Pantula refers to "one aspect of the information technology revolution"—-the "data deluge"—-and the increasing importance of data-intensive research, which he says will "drive many of the major scientific breakthroughs in the coming decades." (In fact, the NSF has recently created a new program, Computational and Data-Enabled Science and Engineering (CDS&E), which is described on their website as "a critical third pillar" of science—-theory and experimentation being the first two—-that is "revolutionizing the way science and engineering are done.")
Andrews also quoted from "the most enthusiastic account of the data deluge" in the media, a 2008 article entitled "The End of Theory: The Data Deluge Makes the Scientific Method Obsolete," written by Wired magazine editor-in-chief Chris Anderson. In the article, Anderson proclaims that there is now a "better way" to do science: "Petabytes allow us to say ‘Correlation is enough.’… We can throw the numbers into the biggest computing clusters the world has ever seen and let statistical algorithms find patterns where science cannot."
 "It is clear that the data deluge is the current wave of the future," concluded Andrews. "The problem is that when ‘waves of the future’ show up they often wash away a number of worthy things and leave a number of questionable items littering the beach." In particular, Andrews suggested "we try to maintain a sense of proportion. While the data deluge is with us, and it’s impact will be great, one unintended consequence is the accompanying unstated implication that nothing is trustworthy if it is not supported by data."
"It is clear that the data deluge is the current wave of the future," concluded Andrews. "The problem is that when ‘waves of the future’ show up they often wash away a number of worthy things and leave a number of questionable items littering the beach." In particular, Andrews suggested "we try to maintain a sense of proportion. While the data deluge is with us, and it’s impact will be great, one unintended consequence is the accompanying unstated implication that nothing is trustworthy if it is not supported by data."
This led Andrews to discuss the role of metrics, the "means by which one can utilize and compare large data sets." He described several metrics, such as the multi-government agency project called STAR METRICS (Measuring the EffecT of Research on Innovation, Competitiveness and Science). He also discussed the journal impact factor, which the authors of a March 2011 Notices article entitled "Nefarious Numbers" argue does not accurately reflect a journal’s quality. Andrews seconded their conclusion by citing two important mathematics papers, the first of which received 2067 citations and the second 28. Both papers are "extremely important in incomparably different ways," he pointed out, and "to suggest by a citation count that the first paper is 70 times more important than the second one is appallingly ridiculous." Andrews reminded the audience of Marshall McLuhan’s oft-quoted statement, "The medium is the message." In explaining the meaning of this statement, Andrews stated that "of central importance is the fact that a medium seeks content that is appropriate to it, and it ignores content that it cannot easily accommodate." He concluded that "we should be aware of the fact that if we are to slide into a world where everything we do is evaluated by metrics applied to certain bean-counting operations, we are stepping into a world where important information is being lost in large amounts."
Andrews devoted the latter part of his talk to the impact of the data deluge on education, specifically the Common Core State Standards for Mathematics (CCSSM). While he would agree that they are a "coherent and mathematically-sound set of K-12 standards," he does have some concerns about the heavy emphasis on certain concepts and the near exclusion of others. For instance, words related to memorization appear very few times in the standards, even though, in the words of an Illinois teacher who wrote to him several years back, "post-comprehension memorization is beneficial to promote efficiency in problem-solving." The word "technology" appears 17 times and "computer" appears 10 times, while "pencil" appears once…in spite of the fact that recent research has shown that writing by hand is better for learning then typing. Andrews concluded, "these concerns, coupled with the co-equal appearances of ‘Probability & Statistics’ with ‘Algebra, Geometry & Arithmetic’ suggest that CCSSM was perhaps insufficiently vigilant in anticipating the effects of the data deluge and its concomitant educational role promoting the extensive use of technology. Thus to some extent CCSSM failed to give due weight to how real human beings actually learn things." Andrews also stressed that, "if the CCSSM has any chance of making serious improvements in mathematics education," all K-12 teachers must receive the necessary professional development. To that end, he concluded his talk by citing eight people "who have undertaken projects with the idea of enhancing content knowledge of teachers in the classroom," and he urged the audience to think about ways they could support these efforts. The slides that accompanied this presentation, which include the names of the eight people he cited at the end of his talk, are online.

(Andrews talks with current AMS President Eric M. Friedlander)
---Claudia Clark
Slideshow from the MAA Undergraduate Poster Session
Mathematics to DIE for: The battle between counting and matching, Jennifer Quinn (University of Washington Tacoma)
 "Let’s get ready to rumble!" is not something normally heard at the Joint Meetings but as Professor Jennifer Quinn of the University of Washington Tacoma warned, this is not your everyday math talk. She began her talk by suggesting that the listeners think of the day’s presentation more like reality TV: Today live from Hynes Ballroom A, "Mathematics’ Deadliest Warriors."
"Let’s get ready to rumble!" is not something normally heard at the Joint Meetings but as Professor Jennifer Quinn of the University of Washington Tacoma warned, this is not your everyday math talk. She began her talk by suggesting that the listeners think of the day’s presentation more like reality TV: Today live from Hynes Ballroom A, "Mathematics’ Deadliest Warriors."
Rather than a talk, the audience watched as a battle unfolded between two cartoon competitors, the Countess and Sir Matchalot. The Countess, a medieval princess type, prefers the method of attack normally associated with one’s fingers and toes, counting. Her go-to trick is counting the same set or value two different ways. Her opponent, Sir Matchalot, dressed like a Run D.M.C.-era MC, prefers to attack in pairs, using cancelling to get the solution. His main mode of attack is the Description, Involution and Exception, aka the D.I.E., Method. The two compete by computing sums. The Countess computes the positive version of the given sum, and Sir Matchalot finds the alternating version.
With the players introduced, the bout begins. There are three rounds each with a different summand: the summations of 1 through n, of C(n,1) through C(n,n) and of the even Fibonacci numbers through F2n. As the competitors are calculating different sums, they are not judged solely on their ability to find an expression for the sum, but on the simplicity and elegance of their results. As every mathematician has their own definition of what makes a good proof, Quinn let her opinionated audience be the judge, breaking out an applause-o-meter after every round to determine the winner.
The crowd was allowed to choose not only the winner but also one of the challenges, making the presentation a choose-your-own-adventure-style talk. After three rounds, one mid-round surprise thrown down by Sir Matchalot, and a lot of clapping, the day ended in a tie. But who will be the victor when you see these titans compete? (Photo of Jennifer Quinn by Laura McHugh, MAA Editorial/Social Media.)
--- Melanie DeVries
AMS-MAA-SIAM Gerald and Judith Porter Public Lecture: Geometric Puzzles: Algorithms and Complexity, Erik Demaine (MIT)
 "I’m Erik Demaine, and I love mathematics!" [applause] "And I want to convince you that you can have lots of fun with mathematics through puzzles." So began Demaine’s presentation during which he took the audience on a "tour" of games and puzzles that for him have been "a great inspiration for doing really fun mathematics" over the last several years. He preceded the tour by explaining that, as a theoretical computer scientist, he is interested in determining the complexity of solving different types of puzzles: as he stated for this all-levels audience, "What problems can be solved by a computer and which problems cannot?" To simplify the basics of the complexity hierarchy, he told the audience to think of "polynomial" as "good" (problems that can be solved efficiently with a computer) and any other terms, such as "NP-hard," as "really hard" (problems that cannot be solved efficiently with a computer). Demaine noted that this type of codifying "gives us a sense as humans what puzzles are really challenging" and what puzzles are easy—at least in principal—to figure out, as well as helping us design new puzzles.
"I’m Erik Demaine, and I love mathematics!" [applause] "And I want to convince you that you can have lots of fun with mathematics through puzzles." So began Demaine’s presentation during which he took the audience on a "tour" of games and puzzles that for him have been "a great inspiration for doing really fun mathematics" over the last several years. He preceded the tour by explaining that, as a theoretical computer scientist, he is interested in determining the complexity of solving different types of puzzles: as he stated for this all-levels audience, "What problems can be solved by a computer and which problems cannot?" To simplify the basics of the complexity hierarchy, he told the audience to think of "polynomial" as "good" (problems that can be solved efficiently with a computer) and any other terms, such as "NP-hard," as "really hard" (problems that cannot be solved efficiently with a computer). Demaine noted that this type of codifying "gives us a sense as humans what puzzles are really challenging" and what puzzles are easy—at least in principal—to figure out, as well as helping us design new puzzles.
Demaine went on to describe a dizzying array of puzzles and games, including Clickomania, Tetris, Rubik’s Cubes, folding puzzles, puzzle fonts, "Mate in 1" games (including Settlers of Catan), sliding-block puzzles, Kaboozle, jigsaw puzzles, coin-sliding puzzles, Dots and Boxes, and dice-rolling puzzles. In each case, Demaine described what is currently known about the computational complexity of the puzzle or game, as well as some open problems. Here are a few examples.
- Even knowing the starting configuration of a Tetris game and all of the pieces that are to come, it is NP-complete to determine if you will survive the game. (This result, published by Demaine and 5 colleagues, lead to Demaine’s being named a "Tetris Master" by the Harvard Tetris Society "in the year 17 anno Tetris," according to the certificate.)
- How many moves are needed to solve the hardest configuration of the Rubik’s Cube? In 2010, an algorithm was found for solving the Rubik’s cube in 20 moves. But how many moves does it take to solve an n x n x n cube? Last year, Demaine and his colleagues determined that the number is on the order of: n2/log n. (The division by log n is related to being able to move certain clusters of cubies—-the name for the individual cubes—-into their correct locations simultaneously.)
- Do you remember the Eternity puzzle, which two mathematicians solved for a million-pound prize in 2000? It turns out that jigsaw puzzles, edge-matching puzzles, and polyform-packing puzzles (such as the Eternity puzzle) are equivalent, and all are NP-complete, i.e., it is likely that no efficient algorithm can solve these types of puzzles in general.
 |
 |
(Photos of Erik Demaine's Porter Lecture by AMS Public Awareness Officer Annette Emerson)
Demaine finished his talk by having children from the audience help him demonstrate the picture-hanging puzzle: how to hang a picture by two or more nails such that removing just one nail drops the picture. See Demaine's website to learn more about his work with games and puzzles.
---Claudia Clark
AMS Session on Non-Academic Employment. Moderated by C. Allen Butler (Daniel H. Wagner Associates, Inc.)
 On Thursday morning the AMS hosted a session on non-academic employment opportunities available to those in the mathematical community. The discussion was led by a panel of mathematical scientists working in government and industry and it drew an overflow crowd of over 250 people. Along with the moderator, panelists were: Grant Boquet, Metron Inc.; Sara Del Valle, Los Alamos National Laboratory; Andy Niedermaier, Jane Street Capital LLC; Bonita Saunders, National Institute of Standards and Technology; and Charles Toll, National Security Agency. They discussed their work environments, how their work differs from academia, and the qualifications and qualities sought in mathematicians applying for positions in these work places. (Photo by AMS Public Awareness Officer Annette Emerson)
On Thursday morning the AMS hosted a session on non-academic employment opportunities available to those in the mathematical community. The discussion was led by a panel of mathematical scientists working in government and industry and it drew an overflow crowd of over 250 people. Along with the moderator, panelists were: Grant Boquet, Metron Inc.; Sara Del Valle, Los Alamos National Laboratory; Andy Niedermaier, Jane Street Capital LLC; Bonita Saunders, National Institute of Standards and Technology; and Charles Toll, National Security Agency. They discussed their work environments, how their work differs from academia, and the qualifications and qualities sought in mathematicians applying for positions in these work places. (Photo by AMS Public Awareness Officer Annette Emerson)
---Anita Benjamin, Assistant Director, AMS Washington Office
MAA Session, Art and Mathematics, Together Again
*A Visual Representation of the Decomposition of Integers into Prime Factors, Margaret E. Kepner
 Many mathematicians would describe the prime numbers as beautiful. Margaret Kepner has demonstrated the beauty of prime (and composite) numbers quite literally with her piece, Prime Goose Chase. During her presentation, Kepner described the thinking that went into creating the piece. She based the structure on a quilt pattern known as "wild goose chase" (or "flying geese"). Each (downward-facing) triangle represents an integer, starting with from 1, the black triangle in the upper left, and ending with 256, the multicolored triangle in the lower right. The first eight prime numbers are different solid colors; these colors are used again, but in a whiter tint for the next eight primes, and so on. Triangles representing square-free composite numbers (such as 6 or 10) contain the colors of the number’s prime factors. Composite numbers that are powers of a single prime contain the prime factor color, as well as increasingly darker horizontal bands of this color: for example, 8 is made up of three red bands of increasingly darker shades. All other composite numbers are represented by a combination of these features. Kepner completed the piece by placing a black background behind each prime, adding some shading around the composites, and connecting multiples of 6 with diagonal grey stripes. (Click on image for a larger version.)
Many mathematicians would describe the prime numbers as beautiful. Margaret Kepner has demonstrated the beauty of prime (and composite) numbers quite literally with her piece, Prime Goose Chase. During her presentation, Kepner described the thinking that went into creating the piece. She based the structure on a quilt pattern known as "wild goose chase" (or "flying geese"). Each (downward-facing) triangle represents an integer, starting with from 1, the black triangle in the upper left, and ending with 256, the multicolored triangle in the lower right. The first eight prime numbers are different solid colors; these colors are used again, but in a whiter tint for the next eight primes, and so on. Triangles representing square-free composite numbers (such as 6 or 10) contain the colors of the number’s prime factors. Composite numbers that are powers of a single prime contain the prime factor color, as well as increasingly darker horizontal bands of this color: for example, 8 is made up of three red bands of increasingly darker shades. All other composite numbers are represented by a combination of these features. Kepner completed the piece by placing a black background behind each prime, adding some shading around the composites, and connecting multiples of 6 with diagonal grey stripes. (Click on image for a larger version.)
*The Projective Ornament of Claude Bragdon, Susan McBurney
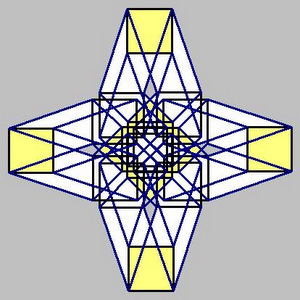 Claude Bragdon (1866—1946) was an architect—a contemporary of architects Frank Lloyd Wright and Louis Sullivan—as well as a philosopher, writer, and later a New York stage designer. However, he is most noted for his work as a designer of a new system of ornamentation, based in geometry, which he described in his book, The Projective Ornament. Bragdon believed that "geometry and number are at the root of every kind of formal beauty." To create his designs, Bragdon would start with the 2-dimensional image of a 3-dimensional projection of one of three 4-dimensional hedroids: the hypertetrahedron, the hypercube, or the hexadecahedroid. He’d then manipulate the image in the plane, select all or part of the design, and finally repeat and possibly enhance the design depending upon its purpose. Susan McBurney designed the ornament shown here by applying this process to a hypercube. (Click on image for a larger version.)
Claude Bragdon (1866—1946) was an architect—a contemporary of architects Frank Lloyd Wright and Louis Sullivan—as well as a philosopher, writer, and later a New York stage designer. However, he is most noted for his work as a designer of a new system of ornamentation, based in geometry, which he described in his book, The Projective Ornament. Bragdon believed that "geometry and number are at the root of every kind of formal beauty." To create his designs, Bragdon would start with the 2-dimensional image of a 3-dimensional projection of one of three 4-dimensional hedroids: the hypertetrahedron, the hypercube, or the hexadecahedroid. He’d then manipulate the image in the plane, select all or part of the design, and finally repeat and possibly enhance the design depending upon its purpose. Susan McBurney designed the ornament shown here by applying this process to a hypercube. (Click on image for a larger version.)
---Claudia Clark
Association for Women in Mathematics Reception
While the stereotype of the anti-social mathematician can be laughable to those in the know, everyone needs a little help meeting new people. The Association for Women in Mathematics Reception after the AMS Gibbs Lecture got everyone up and networking by playing on mathematicians’ natural love of competition and puzzles. They literally turned networking into a game; the game "Set" to be exact. "Set" is a card game popular in mathematical circles. Each card has a colored shape on it. A set is a group of three cards where in each category, shape, color, and shading, each of the three cards are either all the same or all different. The person with the most sets wins.
As the attendees entered, each was given a card on a lanyard and mission: find two other people with who they formed a set. Against a demure background of live piano music and hors d’oeuvres, people pointed at passerby’s chests and yelled, "Set!" For those playing to win, once a set was found the players recorded it along with a few fun facts about their new colleagues. Prizes were awarded for those that managed to collect the most sets. As one might expect, copies of the game were among the winnings.
--- Melanie DeVries
The Design of Intuition: Computing and Mathematical Proof, Stephanie Dick (Harvard University)
Capable of performing quick computations, exhaustively searching for counterexamples, and analyzing intractably large data sets, computers have become invaluable tools in modern mathematical research. As they aid in proving theorems, the natural question is could these logic-based machines be programmed to find new results on their own? Most would object, saying mathematics requires more than knowledge of axioms and logic; it requires creativity and intuition, but can a sufficiently intelligent machine realize these qualities? Stephanie Dick from the Department of History of Science at Harvard University looked at this question through historical attempts to program intuition into machines.
She noted the first theorem-proving programs were just exhaustive searches. These brute force approaches were not surprisingly inefficient with disastrous growth rates, so researchers focused on building computers that worked smarter not harder.
In this talk, Dick compares the perspectives of two research institutions: the RAND Corporation in the 1950’s and Argonne National Laboratory in the 1960’s. The RAND Corporation developed the first smarter or artificially intelligent computer. Alan Newell and Herbert Simon created the Logic Theory Machine, the first program written to recreate a human’s problem-solving skills. It used tricks like working backwards and subproblem chaining to create human-like intuition. The idea was to endow the computer with the ability to guess intelligently. The Logic Theory machine would go on to prove 38 of the first 52 theorems in Whitehead and Russell’s Principia Mathematica.
While the RAND Corporation believed intuition could successfully be programmed, Argonne National Laboratory disagreed. They worked on a system that easily parallels what most mathematicians do today, interactive theorem proving. The computer provides the labor. The mathematician brings the intuition. They used tactics like weighting mechanisms, a process where a mathematician directs the proof search by highlighting paths they believe will be the most profitable, to impose a person’s intuition on a computer’s algorithm.
Even if attempts to recreate intuition were successful, would it be enough? As audience members pointed out, other characteristics, like life experience, also contribute to a strong researcher. Intuition would only be one hurdle towards a virtual mathematician.
--- Melanie DeVries
MAA Session on the History of Mathematics and Its Uses in the Classroom
*Mayan Geometry in the Classroom. Cynthia J. Woodburn (Pittsburg State University)
Cynthia Woodburn began her presentation with a plug for MAA study trips: the hands-on geometry activities she has developed are based on what she learned during the 2011 study trip she took to Guatemala and Honduras. After presenting listeners with a primer on Mayan number symbols, and an introduction to the Mayan calendar, Woodburn described one of the activities: laying out a Mayan house. Maya shamans lay a square foundation, i.e., make right angle corners, using only a special cord divided into 7 equal lengths. How do they do this? Woodburn described the process, which she would have her students—-including middle and secondary school teachers and pre-service teachers—-perform and check using their own chords, chalk, and protractors. Because special ratios, including golden ratios, also appear in Mayan architecture, Woodburn has also designed activities in which students draw these special rectangles using just a cord and then check their drawings using geometry.
*When A Number System Loses Uniqueness: The Case of the Maya, Amy Shell-Gellasch (Beloit College)
In her presentation, Amy Shell-Gellasch described an intriguing aspect of the Mayan number system: some numbers can be represented in two ways. This is due to the fact that their base-20 number system is tied to their calendar system. By the reckoning of one of their calendars, the year is divided up into 18 months, each 20 days in length, plus 5 additional days. Therefore, the first place value in a Mayan number represents the number of days, while the second place value represents the number of days in a month. If we continue this pattern, the third place value represents the number of days in a year—but 20 x 20 is not very close to 365 ! Instead, the third place value is made to represent 18 x 20 (or 360) days in a year. The fourth place value returns to base-20. Thus, the Mayan number 9,7,12,15 equals 9 x 18 x 202 + 7 x 18 x 20 + 12 x 20 + 15, or 67,575. This leads to a lack of uniqueness for certain numbers: for example, 5,19,0 = 6,1,0 and 5,18,0 = 6,0,0. In fact, all numbers whose first two place values range from 18,0 to 19,19 have dual representation.
---Claudia Clark
Rational rationing in healthcare: Observations for organ allocation, Sommer Gentry (U.S. Naval Academy)
Everyone wants the best healthcare for themselves and their families, which makes the idea of rationing healthcare or comparing cost vs. quality life years distasteful at best. The reality is some resources are limited. When it comes to valuable commodities like human organs, no one can deny the demand outmatches the supply. Inspired by her husband’s work at Johns Hopkins, Sommer Gentry of the United States Naval Academy applied discrete mathematics to try to help increase the number of transplants happening every year.
Dialysis can sustain a kidney patient for years, so transplant patients are placed on a single waiting list. But not everyone needs to wait to get to the top of the list. In some cases, a friend or family member will come forward and offer to donate one of their kidneys. The donor’s willingness is not enough however, as blood type and other factors can make a donation impossible. Now imagine there are two couples in this situation. If the donor in couple A is a match for the patient in couple B and vice versa, then the solution is simple, they trade. The idea of these trades, called paired donations, is fairly new and only came into practice in 2005. As the pool of people willing to participate grew, a way to maximize the number of possible paired donations needed to be found.
Gentry attacked the problem from a graph-theoretic perspective. By placing each couple on a node and putting an edge between couples that could trade, she created a graph. Now the problem of maximizing the number of paired donations was reduced to one that was well understood in the math world: finding the largest set of edges where no two edges shared the same vertex, i.e. finding a maximal matching. In 1965, Jack Edmonds created an algorithm that could construct maximal matchings on graphs, solving this version of the problem.
While this finds a maximal number of transplants, it may not find the best ones. Weights rating the predicted success of the transplants are added to the edges of her graph, making the goal to maximize both the number of edges and their total weights. Unfortunately, this is not always possible. The matching with the highest total weight may not have the highest number of edges. Gentry suggests a new point system could help bridge the gap between the two differing goals.
Paired donations are not the only recent innovation. Instead of just looking for two couples who could trade, doctors are also looking for chains of people who can trade i.e. donor A gives their kidney to patient B, donor B gives their kidney to patient C and so on all the way back to A. Mathematically, these chains manifest as cycles in the related graph.
Computationally finding cycles of arbitrary length in graphs can be simple, but the practical issues of cycle donation greatly restricts the acceptable length of a cycle. The greatest hurdle is to ensure that the uncoerced participation of the donors involved in all the surgeries in the cycle are completed at the same time. While John Hopkins has performed a seven-way exchange, the staff and facilities necessary for such a feat are not available everywhere. Furthermore, the greater the number of people involved, the higher the risk that an illness or poor test result will make one of the donations impossible, causing the whole cycle to fall apart. To account for this, Gentry has turned to integer programming to find an optimal search for cycles with maximum lengths of 3 or 4.
[Hear Gentry talk about her research in the Mathematical Moment Matching Vital Needs.]
--- Melanie DeVries
Turning theorems into plays, Steve Abbott (Middlebury College)
With the popularity of film and television programs like Proof, A Beautiful Mind, and Numb3rs, writers have stopped thinking of mathematicians as cold and off-putting characters and have begun to see them as characters a popular audience could relate to. Professor Steve Abbott of Middlebury College‘s presentation looked into how mathematics and mathematicians were being represented in modern theater. Turning his talk in more of an exhibition, Abbott brought in his Middlebury Players (Ele Woods, Adam Milano, Tara Giordano, Alex Draper, and Abbott himself in a quick cameo) to perform selected scenes from various math-centric plays including: Arcadia, Love Song of the Electric Bear, The Five Hysterical Girls Theorem, and Proof.
The first scenes performed were from Arcadia by Tom Stoppard. Arcadia is set simultaneously in the early 1800’s and in present-day England. The story in the past centers on Thomasina Coverly, a bright young woman whose tutor, Septimus Hodge, is educating her in mathematics. In the present, a group of academics occupy the house. Amongst them is a math biologist, Valentine Coverly, who finds and tries to decipher Thomasina’s mathematical writings.
Steve Abbott started the presentation with Arcadia because he regards it as the first play to depict mathematicians as passionate, dynamic characters, putting them in the classically romantic roles more often reserved for poets and historians. The cast put on a scene between Thomasina and Septimus where Septimus tried to distract his young pupil from the definition of carnal embrace by having her attempt to prove Fermat’s Last Theorem. Despite its tameness, Abbott notes with some amusement that the organizers were worried that the sexual content of the scene may not be appropriate for a group of adult mathematicians.
The performance also included a scene in honor of Alan Turing’s upcoming 100th birthday. The selection was from Lovesong of the Electric Bear by Snoo Wilson. Abbott describes the play as being a fairly accurate retelling of the life of Alan Turing including its tragic end save for one element, a main character of the play is Turing’s faithful teddy bear Porgy. The plot has Porgy taking Turing back Scrooge-like through the episodes of his life in the moments before his death. The teddy bear serves as Turing's sounding board and ally throughout the play, grounding the occasionally exceedingly eccentric Turing as an emotional human being. The scene included Turing talking with his bear, portrayed by a Middlebury Player in furry boots and ears, about his universal machines and letting Porgy help him teach his mocking students.
The talk ended with a heart-wrenching scene from Proof by David Auburn. It is the story of the relationship between a father and daughter who are both mathematicians. In the scene, the daughter, Catherine, realizes her father’s mental illness has grown out of control, so she must return from college to once again take care of him. The scene was the first to contain no actual mathematics, but it nicely underscored the theme that it was not so much the mathematics that was attracting playwrights but the passionate and complicated lives of mathematicians.
--- Melanie DeVries
Read more about the Joint Meetings in Adriana Salerno's experiences on the JMM 2012 blog.
More highlights of the 2012 Joint Mathematics Meetings.
Photos on this page, unless identified otherwise, are by E. David Luria.

