Stereographic Projection
In effect, stereographic projection wraps the plane around the sphere, missing only that one point...
 Bill Casselman
Bill Casselman
University of British Columbia, Vancouver, Canada
Email Bill Casselman
Introduction
It is impossible to draw maps of the Earth's surface on a flat surface in such a way that no distortion takes place. Put more mathematically, it is impossible to render paths on a sphere onto a flat surface in such a way that all distances remain the same. In drawing a map of a sphere some compromises must be made. On the other hand, the human eye likes certain properties of the Earth's surface to remain invariant in order to make sense of a map more easily. Most maps adopt one of two possible strategies---that areas are preserved or that angles are preserved. Stereographic projection is one way of making maps, and it adopts the second strategy. It has been used since ancient times for this purpose, and at least one of its basic geometrical properties was known even then.
What is stereographic projection?
Stereographic projection associates to every point $P$ on the sphere, with one exception, a point $P'$ on the plane. Place the unit sphere $x^2 + y^2 + z^2 = 1$ in 3D, and put on top of it the tangent plane $z=1$ at the North Pole. If $P$ is a point on this sphere, the line from the South Pole $\Pi = (0, 0, -1)$ through $P$ will intersect that tangent plane at exactly one point $P'$. We map $P$ to $P'$.
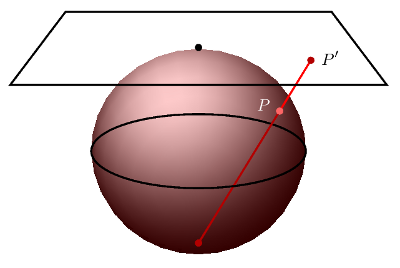

This construction fails only if $P$ is the South Pole itself. In effect, stereographic projection wraps the plane around the sphere, missing only that one point.
It is not hard to find formulas for $P'$ in terms of $P$. If $P = (x, y, z)$ with $x^2 + y^2 + z^2 = 1$, the line through $P$ and $\Pi$ has parametric form $t \mapsto \Pi + t(P - \Pi) = (tx, ty, -1 + t(z+1))$. This intersects $z=1$ for $t = 2/(1+z)$, which gives us $$ P' = (X, Y, 1) \quad \hbox{with}\quad X = { 2x \over 1 + z }, Y = { 2y \over 1 + z } . $$
The inverse map takes $(X, Y)$ to the point $(x, y, z)$ lying on the line through $(X, Y, 1)$ and $\Pi$. Thus we must solve $$ x = sX, \; y = sY, \; z = 2s - 1 \, (\Rightarrow z^2 = 4s^2 - 4s + 1)$$
subject to the condition $$ x^2 + y^2 + z^2 = s^2(X^2 + Y^2 + 4) - 4s + 1 = 1 , \quad s \ne 0 $$
giving $$ s = { 4 \over X^2 + Y^2 + 4 } . $$
It is easy to see that circles of latitude are mapped onto circles in the plane, centered at the North Pole. It is only slightly more difficult to see by a simple geometric argument that circles on the sphere that pass through the North Pole are mapped to straight lines in the plane. It is not quite so easy to see that
Theorem 1. Any circle that does not pass through the North Pole is mapped to a circle on the plane.
This was known to Greek mathematicians of Hellenistic times. More subtle, and not apparently known until the seventeenth century, is this:
Theorem 2. Stereographic projection preserves angles, in the sense that if two curves intersect at an angle $A$ on the sphere, so do their images under stereographic projection.
I'll explain why these theorems are true in the next several sections. In the first of these I'll recall some elementary facts about plane geometry that will be needed later on.
Comments?
Circles in 2D
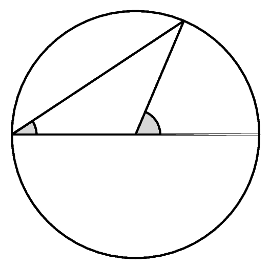
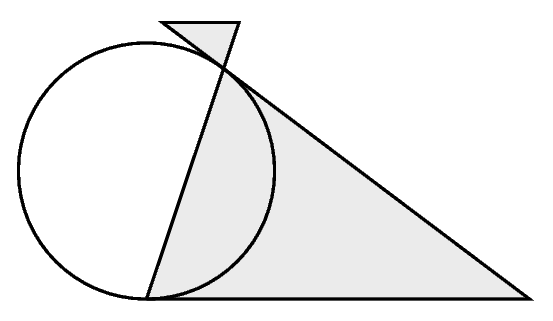
Start with a circle whose diameter is $AB$. For each point $P$ on the circumference, let $P'$ be its projection onto $AB$. The circle whose diameter is $AB$ consists of all points $P$ such that $PP'^{2} = AP' \cdot P'B$.
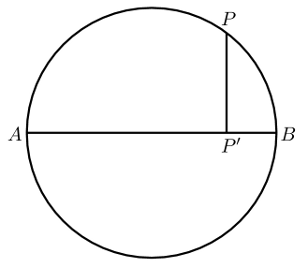
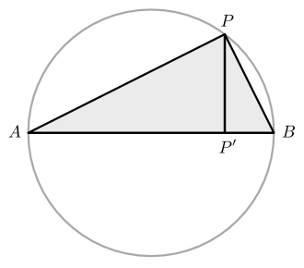
This follows from Pythagoras' Theorem. It can be rephrased as asserting that the triangles in the figure on the right are similar.
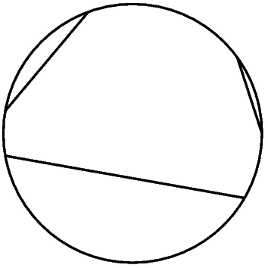
Later on, we'll need to know that all angles in the figure on the left below are the same. This is true because in the figure on the right, the central angle is twice the peripheral one.
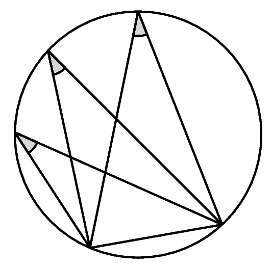
Comments?
Circles in 3D
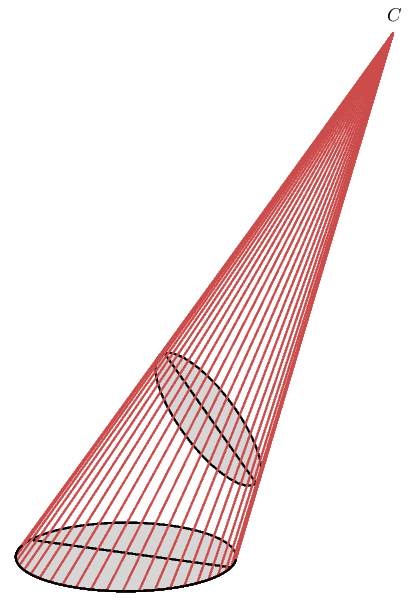
Place a circle in the plane, and choose some point $C$ not in that plane. Construct the cone with $C$ as vertex intersecting the plane in the given circle.

Any section of this cone parallel to the given plane is a circle. If the cone is a right cone--if its axis is perpendicular--then these are the only circular sections. But if this is not the case, there exist conjugate sections that are also circles. In fact, there exists a single family of them, all parallel to each other, as Proposition 5 of Book I of Apollonius' treatise on conics asserts. How does the argument go?

Construct inside the triangle $ABC$ below a contrary triangle $A'B'C$ similar to $ABC$ but with the opposite orientation.
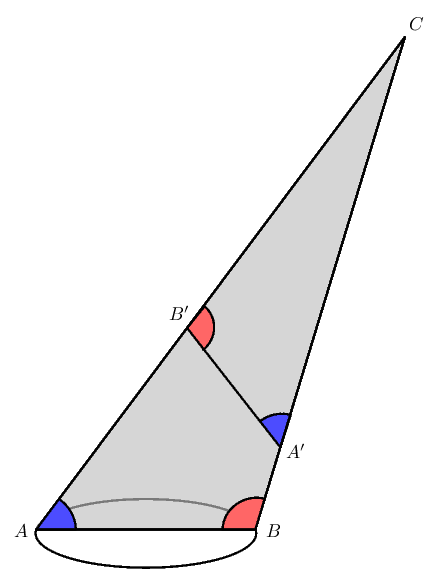
Erect through $A'B'$ a plane perpendicular to it. I claim that the intersection of the cone with this plane is a circle.
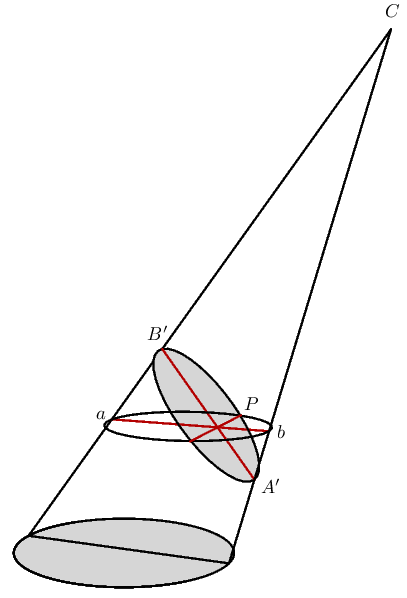
If $P$ is any point of this intersection and $P'$ is the foot of the perpendicular from $P$ to $A'B'$, we must show that $PP'^2 = A'P'\cdot P'B'$. Pass a plane parallel to the original one through the line $PP'$, and let $a$ and $b$ be the points on this plane corresponding to $A$ and $B$. Since this section by this new plane is a circle, we know that $PP'^2 = aP'\cdot P'b$. But the following figures explain why $aP'\cdot P'b = A'P'\cdot P'B'$.

Finally, the next figure shows why this implies Theorem 1.
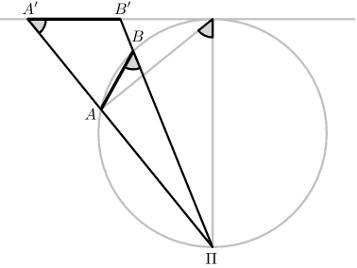
Comments?
This concludes the proof of Theorem 1. This result is one of the first results in Apollonius' book on conics, and presumably one of the earliest non-trivial results known to the Greeks about conic sections.
Angles
Now to deal with Theorem 2.
|
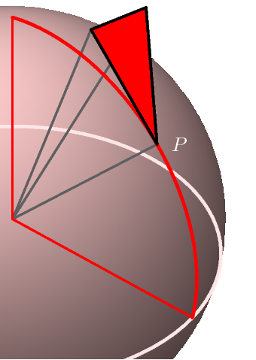
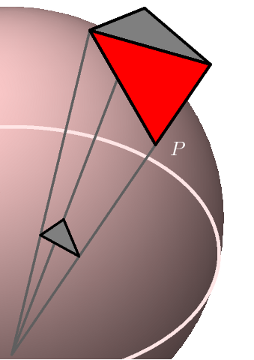
Construct a meridian triangle $T$ at $P$, tangent to the unit sphere, with one right angle.
|
 |
|
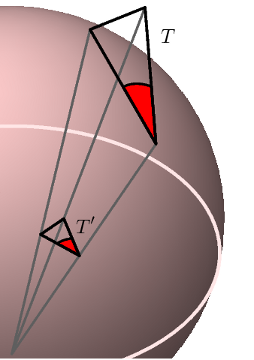
Project it onto the equatorial plane to get a triangle $T'$ which is also right angled. We want to show that $T$ and $T'$ are similar.
|
 |
|
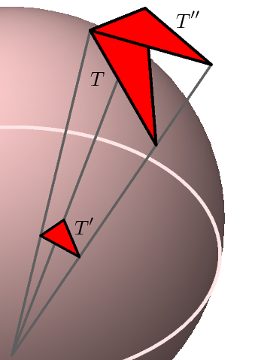
Construct a triangle $T''$ parallel to $T'$, attached to $T$ along the edge opposite $P$.
|
 |
|
It is congruent to the original one, because the colored triangle is isosceles.
|
 |
|
And, finally, a diagram to explain why it is isosceles.
|
 |
Comments?
What is it good for?
Historically, stereographic projection has been used since the Hellenistic era for making sky charts. This was explained first in the treatise On the planisphaerium by Ptolemy, although no instruments from that time are extant. Later on, Ptolemy's technique was applied to make astrolabes, which were used extensively throughout the middle ages, in both the Islamic world and in Europe. In the following photograph, taken from the Wikipedia image collection, you can see two sets of circles of which one is a set of latitudes around the North Star.

http://en.wikipedia.org/wiki/File:Astrolabe-Persian-18C.jpg
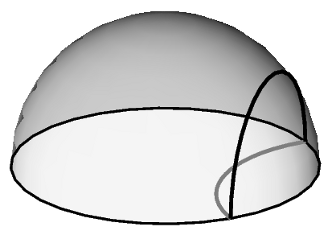
In modern times, it has been used in relating the two well known models of non-Euclidean geometry by configurations in the unit disc. In Klein's model, non-Euclidean geodesics are represented by straight line segments in the interior of the disc. In Poincaré's, they are represented by arcs intersecting the boundary of the disc at right angles.

Stereographic projection allows you to pass from one to the other, after first lifting one of Klein's segments into the hemisphere lying over the disc.
Where to learn more
- Claudius Ptolemy, Planisphaerium. An English translation can be found in the Yale Ph. D. thesis of Christopher Anagnostakis, The Arabic version of Ptolemy's Planisphaerium, dated 1984.
- Apollonius, Conics. Translated by T. L. Heath, Cambridge University Press, 1896.
Available from the California digital library. This is not by any means an exactly accurate translation of Apollonius' text, but it is a good approximation, and fairly readable--probably more readable than a more exact translation would be. Heath's comments are also valuable.
- Lohne, Thomas Harriot als Mathematiker, Centaurus 11 (1) (1965).
This contains a reproduction of Thomas Harriot's elegant graphical proof that stereographic projection preserves angles, whch I have tried to simulate. The British Library contains several books of manuscripts by Harriot, much of which deserve to be published.
 Bill Casselman
Bill Casselman
University of British Columbia, Vancouver, Canada
Email Bill Casselman



 Bill Casselman
Bill Casselman




















