The Topology of Impossible Spaces
The purpose of this month's article is to bring once more to the public consciousness some work of Sir Roger Penrose...
 Tony Phillips
Tony Phillips
Stony Brook University
Email Tony Phillips
Introduction
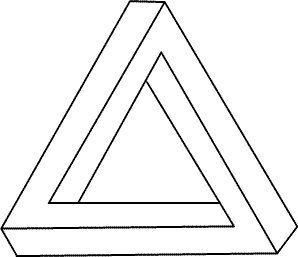
Figure 1. Roger Penrose invented this impossible object, the tribar. It is described (British Journal of Psychology, 1958) in an article he co-authored with his father, the psychiatrist and medical geneticist Lionel Sharples Penrose FRS.
The purpose of this month's article is to bring once more to the public consciousness some work of Sir Roger Penrose, namely "On the Cohomology of Impossible Figures," which appeared in Structural Topology 17 (1961) pp. 11-16 and was reprinted in Leonardo 25, Nos 3/4 (1992) and then as Chapter 4 of The Visual Mind, Michele Emmer, ed., MIT Press, 1993.
The tribar
After inventing the tribar, Penrose found a way to quantify what makes it impossible. Imagine assembling the tribar from the 3 identical L-shaped pieces shown in Fig. 2.
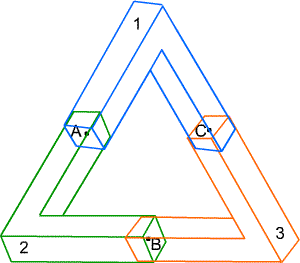
Figure 2. The tribar is assembled from three identical pieces, labeled here 1, 2, 3, and colored blue, green, orange. The pieces overlap; choose a point $A$ in the overlap between 1 and 2, a point $B$ in the overlap between 2 and 3, and a point $C$ in the overlap between 1 and 3.
Choose points $A,B,C$ in the overlaps between the three pieces, and then pull the pieces apart. There will now be a point $A_1$ in 1 and a point $A_2$ in 2, both correponding to $A$, and similarly points $B_2, B_3$ corresponding to $B$ and points $C_1,C_3$ corresponding to $C$, as shown in Fig. 3.
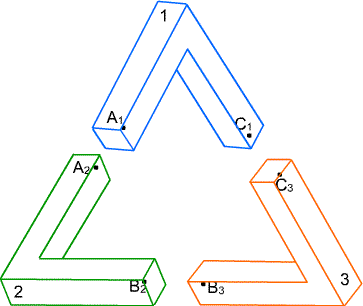
Figure 3. The tribar separated into its three components, with the points $A_1, A_2$ corresponding to $A$, etc.
Now, following Penrose, imagine that 1, 2 are 3 actual objects in space, and that Fig. 3 is an isometric perspective drawing of them. A perspective drawing represents 3-dimensional space in the plane of the picture, and implies that some of the points shown are farther from the eye $E$ of the viewer than others. For example $d(E,A_1)$, the implied distance from $E$ to the point in space $A_1$ may be different from $d(E,A_2)$, the implied distance $E$ to $A_2$.
Set $$d_{12} = \frac{d(E,A_1)}{d(E,A_2)}.$$
In the same way, set $$d_{13} = \frac{d(E,C_1)}{d(E,C_3)},~~~ d_{23} = \frac{d(E,B_2)}{d(E,B_3)}.$$
Ratios $d_{21}$, $d_{31}$, $d_{32}$ can be similarly identified, and $d_{21}= 1/d_{12}$, etc.
Note first that $d_{12}$ does not depend on the points $A_1$ and $A_2$: any two points in 1 and 2, which correspond to the same point in the tribar, would give the same number; likewise for the other $d_{ij}$.
There is an inherent ambiguity in our interpretation of a perspective drawing of an object: it could be twice as big (in linear dimensions) and twice as far away and look exactly the same. Suppose for example we change our mind about how far object 2, for example, is from the eye, and that we change its perceived distance by a factor of $\lambda$. Then by the way the $d_{ij}$ are defined, both $d_{23}$ and $d_{21}$ will be multiplied by $\lambda$, while both $d_{12}$ and $d_{32}$ will be divided by $\lambda$.
Now back to the impossibility of the tribar. Suppose that the pieces 1, 2, 3 could actually be assembled into an object with a coherent existence. Then we could move them forward or back by factors $\lambda_1, \lambda_2, \lambda_3$ to make all the $d_{ij} =1$. As explained in the last paragraph, this means that $$(\lambda_1/\lambda_2)~ d_{12} = 1,~~ (\lambda_1/\lambda_3)~ d_{13} =1,~~ (\lambda_2/\lambda_3)~ d_{23}=1,$$ or $$d_{12}= \frac{\lambda_2}{\lambda_1},~~d_{13}= \frac{\lambda_3}{\lambda_1},~~d_{23}= \frac{\lambda_3}{\lambda_2}.$$ And if there are no such $\lambda_1, \lambda_2, \lambda_3$, then the object is impossible.
Comments?
Cohomological interpretation
As Penrose explains, there is a mathematical formalism that applies here exactly: 1-dimensional cohomology. A slightly simple-minded definition goes like this.
-
Suppose an object $X$ is the union of $n$ subsets $U_1, \dots, U_n$ with the property that each of the $U_i$ is topologically like a solid ball (using 3-dimensional language), and that each of the intersections $U_{ij}=U_i\cap U_j$ is also, topologically, a ball. (These hypotheses work for our tribar, with $U_1 = $1, $U_2 = $2, $U_3 = $3. Note from Fig. 2 that the intersections, those bi-colored cubes surrounding $A, B$ and $C$, are also, topologically, solid balls).
-
A 0-dimensional cochain with values in ${\bf R}^+$, the positive real numbers, assigns such a number, say $\lambda_i$, to each of the $U_i$, and a 1-dimensional cochain assigns a number, say $a_{ij}$, to each of the $U_{ij}$ with the understanding that $a_{ji}=1/a_{ij}$, so $U_{ij}$ and $U_{ji}$, while corresponding to the same set, are accounted for differently. A 2-dimensional cochain would assign a number to each triple intersection, but there are none in this example.
-
If $\lambda_1$, $i=1, \dots, n$ is a 0-cochain, its coboundary $\delta\lambda$ assigns to each $U_{ij}$ the number $\lambda_j/\lambda_i$.
-
To see the pattern, suppose that $X$ does have triple intersections. Then the coboundary of the 1-cochain $\{ a_{ij} \}$ would be the 2-cochain $\delta a$ assigning to $U_{ijk}$ the number $\delta a_{ijk} = a_{ij}a_{jk}/a_{ik}$.
An important consequence of this definition (and of its extension to higher-dimensional cochains) is that $\delta\delta=1$, the unit in our group of coefficients. In fact we can check with what we have: $$\delta\delta\lambda_{ijk} = \delta\lambda_{ij}\delta\lambda_{jk}/\delta\lambda_{ik} = (\lambda_j/\lambda_i)(\lambda_k/\lambda_j)/(\lambda_k/\lambda_i) = 1.$$
Continuing the list of definitions:
-
A cochain with coboundary equal to 1 is called a cocycle; if there are no cochains in the next dimension, then every cochain is considered a cocycle (this happened with 1-cochains on the tribar). It follows from $\delta\delta=1$ that every coboundary is a cocycle. A cocycle which is not a coboundary is topologically interesting, and sometimes called a "non-trivial" cocycle.
-
So for the purposes of this column: If perspective drawing defines an impossible object, then breaking it up into possible pieces (which are topologically solid balls, and whose intersections are also solid balls), choosing points in the intersections and defining the numbers $d_{ij}$ as above leads to a non-trivial cocycle.
-
Penrose mentions the first cohomology group of $X$ with coefficients in ${\bf R}^+$, written $H^1(X,{\bf R}^+)$. Strictly speaking, what we are working with here is the cohomology of the covering ${\cal U}= \{U_1, U_2, U_3, U_{12}, U_{13}, U_{23} \}$ but as soon as the elements of ${\cal U}$ are all solid balls, what we calculate only depends on $X$. The 1-cochains form a multiplicative group ($(ab)_{ij} = a_{ij}b_{ij}$); the 1-cocycles are a subgroup which contains the subgroup of the 1-coboundaries. Everything is abelian so the quotient group (1-cocycles) modulo (1-coboundaries) is defined, and that is $H^1({\cal U},{\bf R}^+)$, which we may call $H^1(X,{\bf R}^+)$.
-
Penrose does not mention the evaluation map, but it helps solidify the relation between impossibility of the object and non-triviality of the cocycle. In our example, the evaluation map $\epsilon$ takes a 1-cochain $d$ to the product $ d_{12}d_{23}d_{31}$, an element of ${\bf R}^+$.
With ${\cal U}$ as above, a 1-cochain $d$ is a coboundary if and only if $\epsilon(d) = 1$. This follows almost immediately from the definition of coboundary, since if there was a 0-cochain $\lambda=\{\lambda_1, \lambda_2, \lambda_3\}$ with $d=\delta\lambda$, i.e., $d_{12}=\lambda_2/\lambda_1$, etc., then in the product $d_{12}d_{23}d_{31}$ all the $\lambda$-factors would cancel. On the other hand, if $d_{12}d_{23}d_{31} = 1$, then one can define $\lambda_1 = 1, \lambda_2 = d_{12}, \lambda_3 = d_{13}$ and get $d=\delta\lambda$: we just need to check $d_{23} = \lambda_3/\lambda_2$, but the ratio is $d_{13}/d_{12}= 1/(d_{31}d_{12})=d_{23}$ because $\epsilon(d)=1$.
Looking at the tribar, with Penrose's definition of $d$, we calculate $$\epsilon(d)= \frac{d(E,A_1)}{d(E,A_2)}\frac{d(E,B_2)}{d(E,B_3)} \frac{d(E,C_3)}{d(E,C_1)}.$$ Examine 1, 2 and 3 two by two: conventional perspective forces $A_1$ to be farther away than $A_2$, and $C_3$ to be farther than $C_1$, while $B_2$ and $B_3$ are at the same distance. Two of the fractions are greater than 1, and one is equal to 1, so their product cannot be 1. So $d$ is a non-trivial cocycle and therefore no matter how the distances are adjusted, the pieces will never fit: the tribar is impossible.
Another example
In "On the Cohomology ...," Penrose gives another example of a visual paradox with an associated cohomology group. A smaller example that is less elegant but easier to analyze can be found in another of Sir Roger's inventions: Penrose tilings, a family of non-periodic tilings of the plane.

Figure 4. A Penrose tiling of the plane by two rhombic shapes. Nicolaas de Bruijn found the most elegant and informative way to describe these tilings: they are 2-dimensional projections of a surface in 5-dimensional space. That surface is made up of squares parallel to the coordinate planes, with adjoining squares perpendicular to each other (all this in 5-space). There are 10 possible orientations for such a square; projected these give the two rhombic shapes, with 5 possible orientations for each of them. In the surface in 5-space, whenever a vertex meets exactly three squares, these must be relatively positioned like three faces of a cube. When the three are projected into the plane, they look like the isometric perspective image of an ordinary 3-dimensional cube. But this interpretation cannot be extended to neighboring tiles. Even though those may be part of another cube, the cubes, interpreted in 3-space, form an "impossible" configuration. Some instances of this phenomenon, which forces our perception of the the tiling to continually shift from one interpretation to another, are highlighted in blue in this figure.
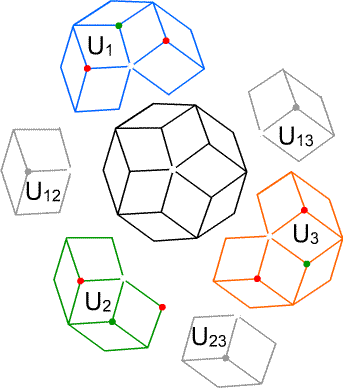
Figure 5. In the central design (the middle highlighted configuration from Fig. 4) it is impossible to interpret all the cubes as being coherently "in" or "out." To describe this phenomenon in the language of cohomology, just as for the tribar, the picture is dissected into three sections (with overlaps), labeled $U_1$, $U_2$, $U_3$, and for which there is no problem. In each of the sections we choose a perception, by requiring that all the red vertices be perceived as "up" (i.e. pointing at the reader) and all the green vertices as "down" (i.e. pointing away). The intersections (overlaps) are shown in grey. The central point has been deleted to avoid triple intersections.
For this structure the natural coefficients are the multiplicative group $\{1,-1\}$ with two elements. A 1-cochain $d$ with these coefficients can be defined by assigning to each intersection the number $+1$ if the two vertices corresponding to the grey vertex are both up or both down. So with the perceptions shown in Fig. 4, $d_{12} = d_{13}=1$ and $d_{23}=-1$.
A new choice of perceptions for the three sections is a 0-cochain $\lambda$ with values in $\{1,-1\}$: If $\lambda_1=1$, segment $U_1$ keeps its original interpretation; if $\lambda_1=-1$, segment $U_1$'s perception gets reversed; and similarly for $\lambda_2$ and $\lambda_3$. Note that if the perception of section $U_1$ is reversed, then both $d_{12}$ and $d_{13}$ get multiplied by $-1$. And if the perception of section $U_3$ is reversed then again $d_{13}$ is divided by $-1$, or multiplied: it's the same since $-1$ is its own multiplicative inverse.
Suppose that the diagram could be coherently apprehended as a union of cubes in 3-dimensonal space. That means that all three sections could be given perceptions which agree on the intersections: there would exist a cochain $\lambda_1, \lambda_2, \lambda_3$ such that $(\lambda_1/\lambda_2)d_{12} = 1$, $~~(\lambda_1/\lambda_3)d_{13} = 1$, $~~(\lambda_2/\lambda_3)d_{23} = 1$. Just as with the tribar (the arithmetic is the same even though the coefficients are different) this implies that $d_{12} = \lambda_2/\lambda_1$, $~~d_{13} = \lambda_3/\lambda_1$, $~~d_{23} = \lambda_3/\lambda_2$, i.e. that $d=\delta\lambda$. Let's check the evaluation map. In this example, its value is in $\{+1,-1\}$. We calculate: $\epsilon(d) = d_{12}d_{23}d_{31} = (1)(-1)(1) = -1.$ So $d$ is a non-trivial cocycle, and therefore the diagram cannot coherently be perceived as a surface made up of squares.
Comments?
Orientation
The most basic way that 1-dimensional cocycles occur in topology is in the study of orientability. Avoiding technical details, let me say that a surface is orientable if there is a coherent, everywhere defined notion of a positive turning direction. Coherent means that a clockwise circle, when dragged to any other point on the surface, will still be perceived as clockwise. The best-known example of a non-orientable space is the Möbius strip.

The Möbius strip is not orientable: a clockwise circle, dragged around the hole, comes back counter-clockwise.
We can proceed exactly as with the "impossible" cube interpretations in the Penrose tiling. The Möbius strip can be covered by 3 rectangles, overlapping two by two in squares. [Note that at least 3 rectangles are necessary for computing cohomology in these circular examples: if there were only two, there would be two separate components to their intersection, so it would no longer be topologically a solid (2-dimensional) ball.]

The obstruction to orientation as a 1-dimensional cocycle. Orientations, i.e. positive turning directions, have been chosen in $U_1$, $U_2$ and $U_3$.
Continuing as in the earlier examples, choose orientations, i.e. positive turning directions, in $U_1$, $U_2$ and $U_3$. Define a 1-cochain $d$ with coefficients in $\{-1,+1\}$ by associating to $U_{12}$ the number $d_{12} = +1$ if the positive orientations on $U_1$ and $U_2$ agree there, and $d_{12} = -1$ otherwise; $d_{13}$ and $d_{23}$ are calculated similarly. In this example, the values would be $d_{12} = d_{23} = +1$, $d_{13}= -1$.
Reversing the orientation in $U_2$, for example, would change the sign of both $d_{12}$ and $d_{23}$; we can think of this as dividing $d_{12}$ by $-1$ and multiplying $d_{23}$ by $-1$. (In the multiplicative group $\{-1,+1\}$, each number is its own inverse, so multiplication and division are the same).
If coherent orientations of $U_1$, $U_2$ and $U_3$ were possible, we could arrange them to match on intersections. The "arrangement" translates to defining a 0-cochain $\lambda$ with coefficients in $\{-1,+1\}$ as follows: $\lambda_1 = +1$ if the orientation on $U_1$ can be left as is, and $=-1$ if it must be reversed. If, after the arrangement, the orientations match on intersections, then $$ 1 = d_{12} \lambda_1/\lambda_2, ~~1 = d_{13} \lambda_1/\lambda_3, ~~1 = d_{23} \lambda_2/\lambda_3,$$ or $$ d_{12} = \lambda_2/\lambda_1, ~~d_{13} = \lambda_3/\lambda_2, ~~d_{23} = \lambda_3/\lambda_2,$$ i.e. $d=\delta\lambda$; the cocycle $d$ is the coboundary $\delta\lambda$. So in this example, non-orientability corresponds to the non-triviality of the "orientation matching" cocycle $d$; and since $\epsilon(d)=(1)(1)(-1)=-1$ (computed exactly as for the tiling example), the surface is non-orientable.
For an example where $d$ is a coboundary, let us add another twist to the Möbius strip.

Adding another twist makes the Möbius strip into an orientable surface.
With the orientations chosen here on $U_1$, $U_2$ and $U_3$, the orientation-matching cocycle is $d_{12} = -1$, $d_{13}=-1$, $d_{23}=1$. Here $\epsilon(d)= (-1)1(-1)=1$ so $d$ is a coboundary. Explicitly, reversing the orientation on $U_1$ makes all the overlaps match; in cohomological terms, $d=\delta\lambda$, where $\lambda_1=-1, \lambda_2=1, \lambda_3=1$.
[Note: Revised 10/2/14]
 Tony Phillips
Tony Phillips
Stony Brook University
Email Tony Phillips



 Tony Phillips
Tony Phillips






