Circles and Squares
Later on, mathematicians took up the much more difficult question, can we find a formula for $r_{k}(n)$, the number of ways to express $n$ as a sum of $k$ integral squares? This last question led to some of the most sophisticated mathematics of the 20th century, as did a common generalization of all these questions....
 Bill Casselman
Bill Casselman
University of British Columbia, Vancouver, Canada
Email Bill Casselman
Introduction
One of the oldest problems in number theory is to determine which integers can be expressed as the sum of two integral squares. An equivalent question is, let $r_{{}_{2}}(n)$ be the number of pairs of integers $(a,b)$ such that $a^2 + b^2 =n$. For example, if $n=5$ the possibilities are $(\pm 2, \pm 1)$ and $(\pm 1, \pm 2)$ so $r_{{}{2}}(5) = 8$. For which $n$ is $r_{{}_{2}}(n) > 0$? This suggests in turn the more general question, can we find a simple formula for $r_{{}_{2}}(n)$?
These problems were alluded to by the mathematician Diophantus in Hellenistic times, and were answered by the French mathematician Pierre Fermat in the seventeenth century. They have been reexamined, along with related questions, by several generations of mathematicians right up to the present. Fermat also had answers to some related questions such as, in how many ways can $n$ be expressed in the integral forms $a^2 +2b^2$ or $a^2 + 3b^2$? Later on, mathematicians took up the much more difficult question, can we find a formula for $r_{k}(n)$, the number of ways to express $n$ as a sum of $k$ integral squares? This last question led to some of the most sophisticated mathematics of the 20th century, as did a common generalization of all these questions. Given a homogeneous algebraic expression $f(x)$, of degree two in $r$ variables with integral coefficients, that always takes non-negative values, can we find a formula for the number of integral solutions of $f(x_{{}_{1}}, \dots, x_{{}_{r}}) = n$ for arbitrary $n > 0$?
The original questions about $r_{{}_{2}}(n)$ are more elementary than the others. There is nothing new to say about them, but for a while each generation had a new and interesting understanding of the answers, generally by placing them in a larger context. Some of these techniques apply also to the other questions, and I am going to try to explain them by seeing what they say about $r_{{}_{2}}(n)$.
The function $r_{{}_{2}}(n)$ may be interpreted geometrically. How many points of the plane with integral coordinates are contained in the band between circles of radii $\sqrt{n\pm 1/2}$ ? One advantage of this interpretation is that it makes it apparent that the complication of the problem is due in some sense to the mutual incompatibility of circles and squares. (Think of all those proverbial square pegs $\dots$ ) It does not, however, suggest how to solve the problem.

What this geometrical interpretation does makes clear is the symmetry of the problem$-$if a solution is rotated around the origin through a right angle, it becomes another solution. The number $r_{{}_{2}}(n)$ (except for $n=0$) is $4$ times the number $\rho_{{}_{2}}(n)$ of integer pairs $(a,b)$ with $a > 0$, $b \ge 0$. Here is a table of some values of $\rho_{{}_{2}}(n)$, expressed in bar graphs:

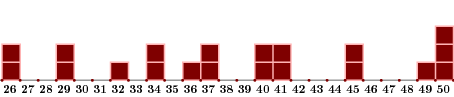
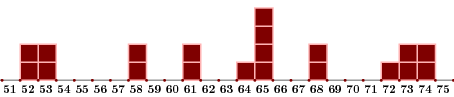

The pattern in this graph is not at all clear, but once a basic principle is perceived, things become clearer. This basic principle is that the function $r_{{}_{2}}(n)$ is related to the multiplicative structure of $n$. More precisely:
| $\bullet$ If $m$ and $n$ is the sum of two integral squares then so is $mn$. |
This can be seen very easily, just by verifying the equation $$ (a^2 + b^2)(c^2 + d^2) = (ac - bd)^2 + (ac + bd)^2 \, . $$
I'll say something later about where this equation comes from. In any case, it suggests that the prime factorization of $n$ will affect $r_{{}_{2}}(n)$, and this in turn suggests presenting the same data but together with the factorization of $n$:




At least one thing ought to become evident. What causes the blanks? Some of them are covered by this claim: If $n \equiv 3 \; (4)$ (by which I mean that $n$ is congruent $3$ modulo $4$, or that $n$ leaves a remainder of $3$ when divided by $4$) then $r_{{}_{2}}(n) = 0$. This is actually very easy to understand. For any integer $c$, $c^{2}$ modulo $4$ is equal to $0$ or $1$, but never $2$ or $3$. Thus $a^{2} + b^{2}$ modulo $4$ is equal to $0$, $1$, or $2$, but never $3$. (This looks simple to us, but when Fermat discovered it he became very excited. Such is progress in technology, if not of human intelligence)
But if you keep studying the table, you will notice a stronger version of this simple fact. If the prime factorization of $n$ has a factor $p^{2k+1}$ with $p \equiv 3 \; (4)$ then $r_{{}_{2}}(n) = 0$. Equivalently:
| $\bullet$ If $r_{{}_{2}}(n) > 0$ then any prime $p \equiv 3 \; (4)$ must occur with even multiplicity in the factorization of $n$. |
The reason for this is a bit more complicated. It depends on a basic fact of number theory that I'll digress to explain. Suppose $M$ for the moment to be any integer $> 1$. If one divides an integer by $M$ then any one of $M$ remainders $0$, $1$, $\dots$ , $M-1$ may occur. These define the set of congruence classes modulo $M$. One can add and multiply such classes - for example if $M =7$ then $3 \cdot 4 = 12 \equiv 5 \; (7)$ so we write $3 \cdot 4 \equiv 5 \; (7)$. A congruence class other than $0$ is called a residue if it is the square of some residue class. Thus the residues modulo $7$ are $1$, $2 \equiv 3\cdot 3$, and $4$, and those modulo $13$ are $1$, $3 \equiv 4\cdot 4$, $4$, $9$, $10 \equiv 6\cdot 6$, and $12 \equiv 5 \cdot 5$. It is a basic fact of number theory that if $p$ is a prime then $p-1 \equiv -1 \; (p)$ is a residue if and only if $p \equiv 1 \; (4)$. Another basic fact of number theory is that in some circumstances one can define the division of congruence classes. More precisely, if $a$ is relatively prime to $M$ then there exists a congruence class $b$ (which I'll often write as $a^{-1}$) such that $a \cdot b \equiv 1 \; (M)$. For example, $2^{-1} \equiv 7 \; (13)$ and $3^{-1} \equiv 9 \; (13)$.
So now suppose $N$ to have a prime factor $p \equiv 3 \; (4)$, and that $N = x^2 + y^2$. Then also $x^2 + y^2 \equiv 0 \; (p)$. If either $x$ or $y$ were relatively prime to $p$, one could divide by it to find $z$ such that $z^{2} + 1 \equiv 0 \; (p)$ or $z^{2} \equiv -1 \; (p)$, which as we have just seen is not possible. Therefore $p$ divides both $x$ and $y$, and $p^{2}$ divides $N$. Continue in this way with $N/p^{2}$, until there are no $p \equiv 3 \; (4)$ dividing $N$.
Thus $3\cdot 7 = 21 \equiv 1 \; (4)$ but even so it cannot be the sum of two squares. A very strong version of this assertion in fact answers the first question at the beginning:
| THEOREM. The positive integer $n$ is a sum of two integral squares$-$i.e. $r_{{}_{2}}(n) > 0$$-$if and only if any prime $p \equiv 3 \; (4)$ occurs with even multiplicity in the factorization of $n$. |
This will be explained in the next few sections.
Comments?
The Gaussian integers
It is possible to give elementary arguments to prove this Theorem, but it is better to apply some advanced technology. This should make the nature of the problem, and in particular possible generalizations, more transparent. Besides, as every carpenter will tell you, solving problems is much easier if you have exactly the right tools at hand.
A Gaussian integer is a complex number of the form $a + b\sqrt{-1} = a+bi$ with $a$ and $b$ integers. They behave formally somewhat like the ordinary integers, in that one can add them and multiply them: $$ (a +bi) + (c + di) = (a+c) + (b+d) i, \quad (a+bi)(c+di) = (ac - bd) + (ad +bc)i \, . $$ Since the late eighteenth century, it has been conventional to identify complex numbers $x+iy$ with points $(x,y)$ in the plane. Adding complex numbers becomes just vector addition. Multiplying them also has a geometric interpretation, but in polar coordinates. Any complex number $x + iy$ can be expressed as $r(\cos \, A + \sin \, A)$ in which $r = \sqrt{x^2 + y^2}$ is the length of the vector$(x,y)$ and $A$ its polar angle. The trigonometry formulas for the cosine and sine of sums of angles then become $$ r(\cos \, A + i \sin \, A) \cdot s(\cos \, B +i \sin \, B) = rs\big(\cos (A+B) + i \sin(A+B)\big) \, . $$ In other words, in compex multiplication lengths are multiplied and angles are added. Multiplication by $i$ itself, for example, amounts to a rotation by $\pi/2$ radians (or $90^{\circ}$).
Define the norm of $x + iy$ to be $$ N(x + iy) = (x+iy)(x-iy) = x^2 + y^2 \, . $$ The complex number $x - iy$ is the conjugate of $x+iy$, denoted $\overline{x+iy}$, and has the property that $\overline{wz} = \overline{w}\,\overline{z}$, which implies immediately that $N(wz) = N(w)N(z)$.
The Gaussian integers may be identified with lattice points in the plane, as in this figure

$-$and $r_{{}_{2}}(n)$ is precisely the number of Gaussian integers $z$ such that $N(z) = n$. Other properties are related to a more interesting fact about Gaussian integers.
|
THEOREM. (Division algorithm) If $n$ and $m \ne 0$ are Gaussian integers, then there exist Gaussian integers $q$ and $r$ with $\Vert r \Vert \le \Vert m \Vert$ such that $n = qm +r$.
|
As Wikipedia says (but alas! doesn't demonstrate) this can be proved graphically, using the geometric interpretation of complex multiplication in terms of rotation.
To familiarize you with the basic idea of the argument, I first use a picture to describe a weak form of the division process for the usual integers: for integers $n$ and $m$ there exist $q$ and $r$ with $|r| < |m|$ such that $n = qm + r$. In a diagram:

The diagram suggests also that our usual conventions are somewhat arbitrary$-$one might equally well write $37 = 4\cdot 8 + 5$ or $37 =5\cdot 8 - 3$. This non-uniqueness also occurs with Gaussian integers, but is again of little importance.
The idea for Gaussian integers is not so different. First I plot all the multiples of $m$. Multiplication by $m$ stretches and rotates, so we get the figure below

and then I add the circles of radius $\Vert m \Vert$ around each multiple, as also in the figure. They evidently cover the plane, so $n$ must lie inside one of them, say the one around $qm$. If $r = n - qm$ then $\Vert r \Vert = \Vert n - qm \Vert < \Vert m \Vert$. Q.E.D.
It should be apparent from the picture that there are a number of choices for $q$ and $r$, some better than others. But as I have already said, that will not be important.
The main consequence of the division algorithm is a variant of prime factorization. Define a unit Gaussian integer to be one whose inverse is also a Gaussian integer. Because lengths are multiplicative, this means that a unit must have length $1$. Therefore the only units are $\pm 1$, $\pm i$.
Define a Gaussian prime to be a Gaussian integer that possesses no divisors except itself and the units. (Note: according to this definition, if $p$ is a prime and $u$ a unit, then so is $up$.) It is easy to see, however, that any Gaussian integer $\pi$ with $\Vert \pi \Vert^{2}$ an integral prime is a prime$-$for example, $1 + i$. But there are others$-$for example, the integer prime $3$ is also a Gaussian prime. This is because if $m$ divides $n$ then $\Vert m \Vert \le \Vert n \Vert$. If $m$ divides $3$ then $\Vert m \Vert^{2} \le \Vert 3 \Vert^{2} = 9$, so if $m$ is a proper divisor then $\Vert m \Vert \le 3$. But a short scan of possibilities will then show that $m$ can be only a unit or a unit times $3$.
|
THEOREM. (Unique factorization) Any Gaussian integer can be expressed as a product of Gaussian primes, which are unique up to a unit factor.
|
The argument that demonstrates this is formally the same as it is for ordinary integers, given the division algorithm. It progresses through a series of Lemmas: (a) The greatest common divisor of two Gaussian integers is well defined; (b) one can apply a Euclidean algorithm to show that $$ {\rm gcd}(a, b) = ka + \ell b \, ; $$ (c) if ${\rm gcd}(a, m) = 1$ and $m | ab$ then $m | b$. One consequence:
| $\bullet$ If $p \equiv 1$ modulo $4$ then there exist $x$, $y$ such that $x^2 + y^2 = p$. |
Proof. There exists $x$ such that $x^2 + 1 \equiv 0$ modulo $p$, so $x^2 + 1 = (x + i)(x-i) = mp$. Factor $x+i$. If $$ x+i = \prod \, \pi_{k} $$ then $p = \prod \, \pi_{k} \overline{\pi}_{k} = \prod \, N(\pi_{k})$. Because $p$ is a prime integer, exactly one of the $N(\pi_{k})$ must be equal to $p$, which means $p$ is a sum of squares.
The factorization is not all that useful unless we know what the Gaussian primes are. They are all listed here (up to unit factors):
|
THEOREM. (a) The Gaussian integers $1 \pm i$ are the primes dividing $2$. (b) Every prime integer $p$ with $p \equiv 3$ modulo $4$ is a Gaussian prime. (c) Every $p \equiv 1$ modulo $4$ can be expressed as a sum $a^2 + b^2$, and then $a \pm bi$ are the Gaussian primes dividing $p$.
|
Comments?
Back to sums of squares
I can now explain a simple formula for $r_{{}_{2}}(n)$.
|
THEOREM. If $n < 0$ then $r_{{}_{2}}(n) = 0$. If $n > 0$, suppose its prime factorization to be $$ n = 2^{j} p_{1}^{k_{1}} \dots p_{r}^{k_{r}} q_{1}^{\ell_{1}} \dots q_{s}^{\ell_{r}} $$
with $p_{i} \equiv 1$ and $q_{i} \equiv 3 \; (4)$. If one $\ell_{i}$ is odd, then $r_{{}_{2}}(n) = 0$. Otherwise $$ r_{{}_{2}}(n) = 4(k_{{}_{1}}+1)\dots (k_{{}_{r}}+1) \, . $$
|
Of course, the first statement is hardly deep. But as we shall see, it fits in well with the conditions on prime factors of $n$.
The idea of a proof of the theorem is natural, given unique factorization of Gaussian integers. Suppose we know that $n = x^2 + y^2$ for some $(x, y)$. We may write (in notation slightly different from the Theorem) $$n = x^2 + y^2 = (x+iy)(x-iy) = (1+i)^{j}(1-i)^{j} \prod_{p_{i} \equiv 1} \pi_{i}^{k_{i}} \overline{\pi}_{i}^{k_{i}} \prod_{q_{i} \equiv 3} q_{i}^{2\ell_{i}} \, . $$
We can use this factorization to find all $a + ib$ with $p = a^2 + b^2$. We do this by writing out $a + ib$ as a product of Gaussian primes, according to these rules. It will be a product of four terms: $\varepsilon \rho_{2}\rho_{1}\rho_{3}$. (a) The term $\varepsilon$ will be a Gaussian unit. The term $\rho_{i}$ will be a product of Gaussian primes of parity $i$ modulo $4$. (b) The term $\rho_{2}$ will just be $(1+i)^{j}$. (c) The term $\rho_{3}$ will just be $\prod q_{i}$. (d) Suppose there are $r$ Gaussian primes $\pi_{i}$ in the factorization of $x+iy$. The term $\rho_{1}$ will be itself a product of $r$ terms. Each of them will be of the form $\prod \pi_{i}^{d} \,\,\overline{\pi}_{i}^{k_{i}-d}$ for $0 \le d \le k_{i}$.
Sure enough, that gives us $$ 4 (k_{1}+1) \dots (k_{r}+1) $$ possibilities in all.
Example. Say $n = 5$. It factors as $(2+i)(2-i)$. And then we can modify each factor by a unit. This gives $r_{{}_{2}}(5) = 8$. This is true for all primes $p \equiv 1$ modulo $4$.
Example. Say $n = 9 = 3^2$. The possible prime factors of $3$ are $\pm 3$, $\pm 3i$, giving $r_{{}_{2}}(9) = 4$ This remains valid for all integer primes $p \equiv 3$.
Example. Say $n = 125 = 5^3 = (1+i)^{3}(1-i)^{3}$. The possibilities are unit times $$ \eqalign { & (1+i)(1+i)(1+i) \cr &(1+i)(1+i)(1-i) \cr &(1+i)(1-i)(1-i) \, . \cr &(1-i)(1-i)(1-i) \, . \cr } $$ So $r_{{}_{2}}(125) = 4 \cdot 4 = 16$.
There is another way to write this formula. Let $d_{{}_{1}}(n)$ be the sum of divisors of $n$ that are $\equiv 1 \; (4)$, $d_{{}_{3}}(n)$ the sum of those $\equiv 3 \; (4)$.
|
THEOREM. (Divisor formula) If $n > 0$ then $r_{{}_{2}}(n) = d_{{}_{1}}(n) - d_{{}_{3}}(n)$.
|
More about these formulas
At first one's impression is that the multiplicative structure of the function $r_{{}_{2}}(n)$ is relevant only to the very special problem of understanding sums of squares, or near relatives. The reasoning that led to its verification depends strongly on unique factorization in the Gaussian integers, certainly. Similar reasoning applies almost without modification to a few other simple problems, for example, the analogous questions involving $x^{2} + 2y^{2}$ and $x^{2} + xy + y^{2}$. Similar techniques even apply to $x^{2} + y^2 + z^2 + w^2$, for which one applies a theory of quaternion integers $a + bi + cj + dk$ (I mean the quaternions defined by the Irish physicist Hamilton). But there was a thread started by the German mathematician Eisenstein, continued most significantly by Hermann Minkowski and Carl Ludwig Siegel, that showed how a multiplicative structure arose when answering this extremely general question: Suppose $$ Q(x) = a_{{}_{1,1}} x_{{}_{1}}^{2} + \cdots + a_{i,j} x_{{}_{i}}x_{{}_{j}} + \cdots a_{r,r}x_{{}_{r}}^{2} $$ to be any algebraic function homogeneous of degree $2$$-$called a quadratic form$-$ with integral coefficients. Can one find a formula for the number of integral solutions $(x_{i})$ of the equation $Q(x) = n$ as a function of $n$? The simplest and perhaps most attractive examples would be the sums of squares $$ x_{{}_{1}}^{2} + \cdots + x_{{}_{r}}^{2} $$ on which many mathematicians throughout the nineteenth and early twentieth century, including the Indian mathematician Ramanujan, worked. What might be considered the definitive answer was found by Carl Ludwig Siegel. It has a few subtle properties, and involves some new ideas. On the one hand, it asserts that in some sense one cannot expect a simple formula for $r_{Q}(n)$, and on the other at the same time it explains fairly precisely why not. At least, it does give a product formula of some kind.
If $M > 0$ is any integer, one may consider the expression $Q(x)$ with coefficients reduced modulo $M$. One can define in an essentially natural way what it means for two quadratic forms to be equivalent as integral expressions, and one can also define equivalence modulo $M$. In some cases, for example $Q = x^2 + y^2$, it turns out that the two notions are the same$-$if $Q$ is any form $Ax^2 + Bxy + Cy^2$ that is equivalent to $x^2 +y^2$ modulo every $M$, then $Q$ and $x^2 + y^2$ are integrally equivalent. Two forms are said to be in the same class if they are integrally equivalent, and in the same genus if equivalent modulo all $M$. Siegel's formula gives a product expression for a kind of average of $r_{{}_{Q}}(n)$ as $Q$ varies over a set of representatives of the forms in the same genus of $Q$, which is finite.
What is the product expression? For each prime $M$, let $N_{M}(Q, n)$ be the number of solutions of $Q(x) = n$ modulo $M$. According to the Chinese remainder theorem, if $M = \prod p_{i}^{k_{i}}$ then $$ N_{{}_{M}}(Q, n) = \prod_{p} N_{p^{k_{i}}}(Q, n) \, . $$ It turns out that for large enough $k$ the number $$ \alpha_{p}(Q, n) = { N_{p^{k}}(Q, n) \over p^{k(r-1)} } $$ does not depend on $k$. For all but a finite number of $p$ it is in fact constant for all $k > 0$. Siegel's result is that the average value of $N_{\Bbb Z}(Q, n)$ over representatives of genera (plural of genus) in a class is equal to the product of a certain surface volume of an ellipsoid in ${\Bbb R}^{r}$ that depends on $n$ and the infinite product $$ \prod_{p} \alpha_{Q,p} $$ which, although infinite, converges to something finite. For $Q = x^2 +y^2$ and $n \equiv 1 \; (4)$, where $n$ is itself a prime, some interesting calculation shows that the total expression becomes $$ 2 \pi \prod_{p} \, \left ( 1 - {\chi(p) \over p} \right ) $$ where $$ \chi(p) = \cases { \phantom{-}0 & if $p = 2$ \cr \phantom{-} 1 & if $p \equiv 1 \; (4)$ \cr -1 & if $p \equiv 3 \; (4)$ . \cr } $$ According to something observed first by Euler, the infinite product is $$ { 1 \over 1 - 1/3 + 1/5 - 1/7 + \cdots \ } $$ and the denominator is $\pi/4$ according to a calculus formula due to Leibniz: $$ \arctan (1) = 1 - 1/3 + 1/5 - 1/7 + \cdots = \pi/4 \, . $$ This therefore gives $r_{2}(n) = 8$, as it should.
The divisor formula was first found by the nineteenth century German mathematician Jacobi. It, too, has a subsequent history. I won't give details, but just say that it leads, not to an exact formula for $r_{_{\Bbb Z}}(Q, n)$ but to an asymptotic formula that gives a good approximation for large $n$. The error in this asymptotic approximation has been of great interest$-$that for $r_{24}(n)$, for example, has an error term involving the famous numbers $\tau(n)$ of Ramanujan, and its magnitude was the motivation for much mathematics in the twentieth century.
Comments?
- A later Feature Column, "Circles and Squares ... and Primes"
- Harold Davenport, The higher arithmetic, published by Harper & Row in 1960.
Chapter 5 is very readable.
- G. H. Hardy, Ramanujan, originally published by Cambridge University Press in 1939. Now available in a reprint from the American Mathematical Society.
A survey of Ramanujan's mathematical work. Originally published in 1940 by the Cambridge University Press, but available now from the American Mathematical Society. The relevant chapters are IX and X. It is not easy to read carefully (the use of so many series is now out of fashion, and maybe even when Hardy wrote this), but segments are valuable. Chapters IX and X are about expressions for $r_{\Bbb Z}(Q, n)$.
Incidentally, Chapter V is about another mathematical problem concerned with counting lattice points on circles$-$to find the true asymptotic estimate for the number of lattice points inside the circle of radius $r$ as $r \rightarrow \infty$. Results on this haven't come even close to what is undoubtedly the correct conjecture. Among really difficult mathematical problems that are simple to state, this must rank as one of the most attractive.
- G.H. Hardy and E.M. Wright, An introduction to the theory of numbers. published in many editions by Oxford University Press.
A still admirable book. Section 16.9 of editions at least up to the 4th discusses the formulas for $r_{2}(n)$. (This discussion is independent of the later chapter on sums of squares.)
- Carl Ludwig Siegel, Lectures on the analytical theory of quadratic forms, from notes by Morgan Ward taken during a course in Göttingen in 1934/35.
This is not light reading, but the initial chapters are not too formidable. It is also difficult to find. There seems to be no elementary account of Siegel's formula, although to explain the formula (as opposed to proving it), is not difficult, and even fascinating in so far as it brings many aspects of mathematics together in this one place. One reason for the lack in exposition might be that Siegel's formula became merged into a main stream of modern analytical number theory, the subject of Tamagawa numbers, which then became the primary focus.
- André Weil, Number Theory, Birkhäuser, 1990.
Despite the title, this is hardly an elementary text book. It is instead an account of the history of number theory from prehistorical times through the late eighteenth century. The author has worked hard at trying to achieve a balance between explaining things in terms of the period and in more modern terms. Not easy to read in detail, but pleasant to skim for mathematical gossip.
- Wikipedia: 15 and 290
As I have said, research on representations of integers by quadratic forms continues to the present.
- Wikipedia: Gaussian integers
- Wikipedia: Ramanujan's conjecture
 Bill Casselman
Bill Casselman
University of British Columbia, Vancouver, Canada
Email Bill Casselman


 Bill Casselman
Bill Casselman










