Understanding Kepler III--Predecessors
How Kepler's predecessors understood the apparent motion of the Sun is what I shall investigate in this column...
 Bill Casselman
Bill Casselman
University of British Columbia, Vancouver, Canada
Email Bill Casselman
This is the third in what I intend to be a series of columns in which I try to illuminate at least parts of Johannes Kepler's derivation of his famous laws of planetary motion. (The first two columns are referenced below.)
Otto Neugebauer has asserted (in his book The exact sciences in antiquity) that "one cannot read a single chapter in Copernicus or Kepler without a thorough knowledge of Ptolemy's Almagest." This is already so even if one wants to understand what is probably at once the simplest and most important feature of Earth-based astronomy, the apparent motion of the Sun. That is what I shall investigate in this column.
The simple eccentric model for the Sun's motion
The orbit of the Earth is, for all practical purposes, an almost circular ellipse with the Sun at one focus. Since the axis of daily rotation of the earth is not perpendicular to the plane of its rotation around the Sun, this plane ellipse is not the same as the plane passing through the Earth's equator. This is what causes our seasons. There are four distinctive points on the orbit related to this feature. For those in the northern hemisphere, these are: (1) the summer solstice, when the Sun reaches its highest point in the sky, and when the sun rises and sets furthest north on the horizon; (2) the winter solstice, when it reaches its lowest point, and the sun rises and sets furthest south; (3) and (4) the spring and autumn equinoxes, which are the moments when the Sun crosses the equator and switches from one hemisphere to the other. (You can find a nice photograph recording these here.) These divisions are characterized by the fact that in each of the quarters they separate the Sun's position in the background of fixed stars by $90^{\circ}$.
The time taken by the Sun in traversing these four periods is not the same:
- autumn equinox to winter solstice: 89.8 days
- winter solstice to spring equinox: 89.0 days
- spring equinox to summer solstice: 92.8 days
- summer solstice to autumn equinox: 93.7 days
In other words, the angular velocity of the Sun as seen from Earth is greatest during the winter and slowest during the summer.
This is not at all immediately apparent in normal life. It is an extremely subtle phenomenon, and it is remarkable that this was discovered by Babylonian astronomers more than two thousand years ago, and subsequently taken into account in detailed computations by the Greek astronomer Hipparchus about 150 BCE.
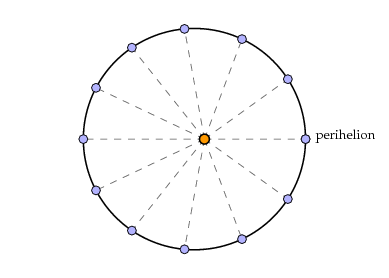
In modern terms, the explanation is well known. Every planet in the solar system travels in an elliptical orbit with the Sun at one focus of the ellipse. It travels fastest when it is closest to the Sun, at the point called its perihelion. The following figure illustrates this for a fictitious Earth whose elliptical orbit has an eccentricity of $0.16$. (This is in between the eccentricities of Mars and Mercury, and I do this exaggeration in order to illustrate features that might otherwise be difficult to perceive.)
Greek astronomers saw things differently, since they believed that the Sun rotated around the Earth. Mathematically, this is an equivalent description of how things go.
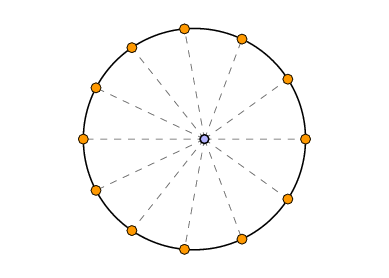
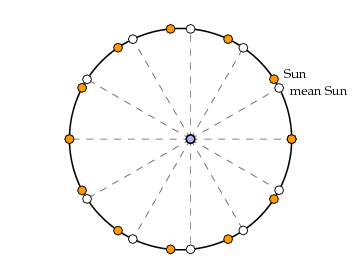
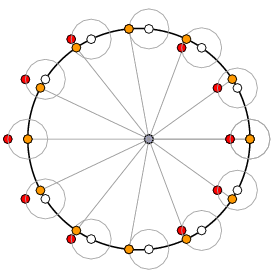
To understand what is going on, Greek astronomers introduced a very useful notion. The motion of the Sun around the Earth is not uniform--sometimes it speeds up, sometimes it slows down. The variation in speed could be pictured by comparing it to an imaginary body called the mean Sun, that did move at a constant angular velocity. In the figure below it is the blank disk.
Near perihelion the mean Sun travels slower than the real one, but as it traverses its orbit the real Sun slows down, and finally at aphelion (when the Sun and Earth are farthest apart) the two again coincide. In the second half of the orbit the mean Sun is ahead of the real one. But now one can visualize fairly well what the problem is--can one find a good approximation to the difference between the real Sun and the mean Sun?
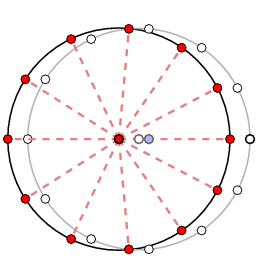
It was apparently Hipparchus who discovered a rather neat answer to this question. The mean Sun is very easy to locate. The real Sun appears to oscillate around it, with a period equal to exactly one year. Now the Greeks were very familiar with the idea of modeling oscillation by means of a rotating object. It was very natural for them to model this oscillation by some kind of rotation on a small circle centered on the mean Sun. In fact, no rotation is necessary. If one draws around the mean Sun a suitable small circle and plots on this a second fictitious body just to the left of the mean Sun (colored red below), then the direction of this new body is extremely close to that of the real Sun. This was a remarkable discovery, since it let Greek astronomers approximate the apparent position of the Sun in the sky, which was something they did not know how to calculate exactly, by something that was very easy to calculate.
Applying what we now know, we can in fact plot the difference in angle between the real Sun and the new approximation. For Earth (the real Earth) the maximum error is about a fifth of one degree.
There are actually two completely equivalent ways to think of this. One is to see it as a kind of trivial rotation on a small circle that was itself rotating in a large circle. The other is to see it as travel around a circle at constant speed, but for which the Earth was not the center.
This model for the motion of the Sun as seen from Earth is known as the simple eccentric model. To us there is no difference between the two artificial constructions--eccentric or epicyclic--but to Copernicus, at least, they were distinct. He writes somewhere, "... it is not easy to see which of them exists in the heavens."
This model satisfies one major criterion of ancient Greek astronomy that might be called `philosophical', since it was most firmly enunciated by Aristotle--the motion of the Sun was at a constant rate around a circle. This is because objects in the sky were thought to rotate on solid spheres, and what other form of motion could be imagined? It was not considered important that the Earth was not located at the center of that circle.
For the Greek astronomers there was one problem I haven't mentioned. Granted that an eccentric model of the Sun's motion was what was wanted, how did one find the parameters of the model? In other words, there is a large family of possible motions. In order to specify one, the direction of the Sun when it moved most rapidly must be found, and also the amount of shift relative to the radius of the circle. The actual size did not matter, only the relative size, because the Greeks were interested only in how things appeared to an observer on Earth. This meant they cared only about direction, not distance. At various points in time they tried to measure the distance from Earth to Sun by measuring daily parallax, but their observational accuracy was far too low (to an angular separation of no better than $1/6$ of a degree) to give a good estimate.
It turns out that that the two parameters of the model are determined by the lengths of any two consecutive seasons. It was Hipparchus who discovered (invented?) this model, and it was he who first proposed parameters. His method and his conclusions were later adopted by Ptolemy (c. 150 CE). There is an interesting story behind this, but not one to be told here.
The equant model
The simple eccentric model predicts the direction of the Sun quite accurately, but makes egregious errors in predicting the distance of the Sun from the Earth. This was not evidently a problem for Greek astronomers. However, as we now know, in observing other planets one has to take into account the precise orbit of the Earth traveling around the Sun, since the Earth is the moving platform from which we make observations. We would therefore expect that in proposing to describe the motion of a planet from Earth, even the Greeks had in some way to deal with this problem. This is indeed the case for Ptolemy's planetary theory, which dealt with it in more than one way. There is a qualitative difference between how the outer planets Mars, Jupiter, and Saturn traverse the sky in comparison to the inner planets Mercury and Venus. The inner planets seem just to oscillate back and forth around the Sun, while the trajectories of the outer planets include occasional oscillations in loops against a dark sky. For the outer planets, Ptolemy used (implicitly) a simple eccentric model. More interesting is how he dealt with Venus.
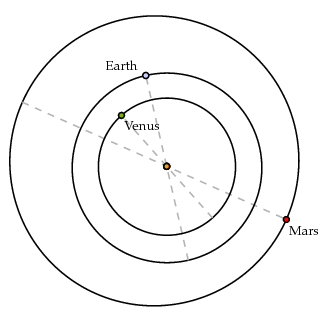
The figure below illustrates (to scale) the orbits of Venus, Earth, and Mars. The dashed lines show their semi-major axes. One thing it shows is that the orbit of Mars possesses a noticeable eccentricity, while those of Venus and Earth are very nearly centered on the Sun.
One might expect that one could approximate the motions in a constant angular velocity around the Sun. We have seen that this is not the case for Earth, but we have also seen that the way in which this fails is rather subtle. What might be a bit surprising is that in observing Venus the effect becomes much more evident. In fact, anyone making measurements of the movement of Venus in the sky would soon realize that something complicated was going on.
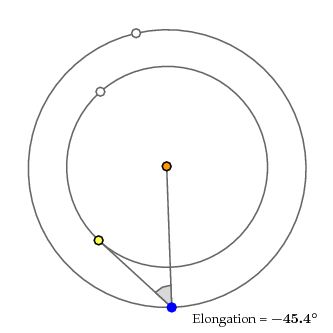
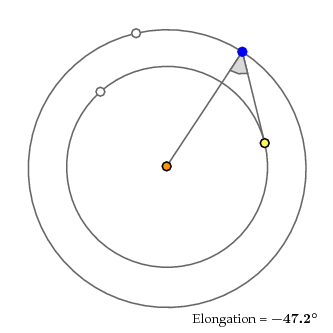
This is measured by the apparent distance between Venus and the Sun, what is called its solar elongation. In some configurations, it can be as much as $47.2^\circ$, and in others as low as $45.4^\circ$. That's a difference of $1.5^\circ$. Since the diameter of the Sun is about $0.5^\circ$, that's a very visible difference. The eccentricity of Venus is about $0.007$, which is very small, so it is the orbit of Earth that is responsible for this range. This is an effect that depends not only on the direction of the Sun as seen from Earth, but also its distance, and the simple eccentric model is no longer sufficient.
Ptolemy was apparently aware of this, one can guess only after a lot of work. To compute the elongations of Venus he introduced a new model, one involving an equant. In this model, the Sun still travels in a circle, and it travels at uniform angular velocity with respect to some point, but the second point, which we call the equant, is no longer the center of the orbit. Instead, the equant and the location of the Earth are displaced at equal distances from the circle's center. The motion of the Sun according to the equant model is composed with an epicycle to locate Venus as a function of time. In the following figure, the arrows denote rotation at constant angular velocity.
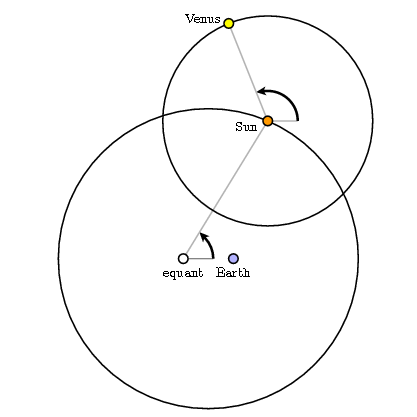
There are a number of remarkable things about this model. When applying it to Venus, we see the equant as the component modeling the motion of the Sun, and the epicycle as modeling that of Venus around the Sun. There is no indication whatsoever that Ptolemy saw things in this way. The same model was used for the outer planets, but for them the equant would appear to us as modeling the motion of the outer planet alone, and the epicycle as modeling the motion of the Earth around the Sun. I am not aware that Ptolemy ever related the two different models for Earth's motion, except that, as someone has remarked, it was a postulate of Ptolemy that the periods of the two were the same. I suppose that this was not considered so noteworthy, considering that the Sun clearly influenced all of our solar system.
But what is truly remarkable, in light of the subsequent history, is that Ptolemy's equant model provides an excellent first-order approximation to Kepler's description of orbital motion. Indeed, Kepler's exploration of the solar system began by replacing the simple eccentric model of the Sun's motion by an equant model for the equivalent motion of Earth, because in order to track the motion of Mars he needed to know very accurately the motion of his observation platform, the Earth.
Ptolemy's models remained in vogue, with a few alterations, for a very long time. The first major alteration to occur in Europe was by Copernicus, who reworked the whole theory--or who, at least, intended to do that. He certainly spent a great deal of effort at this project, but he is one of the grand enigmas in the history of science. His basic idea was that the motion of the planets, as seen from Earth, could be separated distinctly into two components, the motion of the Earth around the Sun and that of the planet. But in practice he failed to carry out this idea thoroughly. He was bothered by Ptolemy's application of equants, and he adapted an idea due to earlier Islamic astronomers that managed to produce essentially the same motions with a mechanism that did in fact restrict itself to circular rotations at uniform speed. But this just reproduced Ptolemy's computations in a different guise. In particular, he used the simple eccentric model to describe the motion of the Earth around the Sun, although updating Ptolemy's data, and he used the same basic mechanism to describe the motion of Venus and the outer planets. This means that on the one hand he was proposing that the Earth was a planet just like the other planets, and on the other retaining the special status that Ptolemy gave it. It is hard to understand what was going on in his mind.
It was only Kepler who first understood the point of the basic Copernican proposal. He was the first to propose plotting true orbits.
Reading further
Light reading
- Arthur Koestler, The sleepwalkers. Penguin, 1964.
An intriguing history of astronomy up to the time of Galileo by an author famous for more literary works. Noted for a novelistic approach to history and for an extremely critical view of Copernicus. But as Owen Gingerich has remarked, many have found it, in spite of its faults, a fascinating and highly stimulating read.
- Asger Aaboe, Episodes from the early history of astronomy, Springer, 2001.
Part II of his article `On Babylonian planetary theories', in Centaurus (1958) has a clearer account of Ptolemy's models of planetary motion.
- Otto Neugebauer, The exact sciences in antiquity. Brown University Press, 1957. Reprinted by Dover.
Appendix I is a useful summary of Ptolemy's system.
- Understanding Kepler I and II
Earlier columns on related material.
Heavy reading
- Ptolemy's almagest. English translation by G. Toomer, published by Princeton University, 1998.
- Otto Neugebauer, On the planetary theory of Copernicus, in the collection Astronomy and history--selected essays. published by Springer-Verlag, 2983.
A short and authoritative if somewhat technical summary.
- Otto Neugebauer and Noel Swerdlow, Mathematical astronomy in Copernicus's `De revolutionibus'. Published by Springer-Verlag, 1984.
Largely quite technical, but also containing readable summaries.
 Bill Casselman
Bill Casselman
University of British Columbia, Vancouver, Canada
Email Bill Casselman


 Bill Casselman
Bill Casselman