Transmitting Data with Polar Codes
This then is the significance of Arikan's polar codes: they provide encodings for an important class of channels that enable us to transmit information at the greatest possible rate and with an arbitrarily small error rate. ...
Introduction
Wireless communication is currently transitioning to a new 5G standard that promises, among other advantages, faster speeds. One reason for the improvement, as we'll explain here, is the use of polar codes, which were first introduced by Erdal Arikan in 2009 and which are optimal in a specific information-theoretic sense.
This column is a natural continuation of an earlier column that described Shannon's theory of information. To quickly recap, we considered an information source $X$ to be a set of symbols $\cx$, such as letters in an alphabet, that are generated with a specific frequency $p(x)$. The amount of information generated by this source is measured by the Shannon entropy: $$ H(X) = -\sum_x p(x)\lg p(x). $$
A simple example is an information source consisting of two symbols, such as 0, which is generated with probability $p$, and 1, generated with probability $1-p$. In this case, the Shannon entropy is $$ H(p) = - p\lg(p) -(1-p)\lg(1-p). $$
We described $H(X)$ as a measure of the freedom of expression created by the source. If $p=1$, then the source can only generate a string of 0's, so there is only one possible message created by this source; it therefore conveys no information. On the other hand, when $p=1/2$, each symbol is equally possible so any string of 0's and 1's is equally likely. There are many possible messages, each of which is equally likely, so a given message can contain a specific meaning, and we think of this as a high-information source.
Entropy is measured in units of bits per symbol. However, if we imagine that one symbol is generated per unit time, we may also think of entropy--measured in bits per unit time--as measuring the rate at which information is generated. We earlier saw how this interpretation helped us determine the maximum rate at which messages generated by the source could be transmitted over a noiseless channel, a fact that is particularly relevant for us here.
Polar codes were created to maximize the rate at which information can be transmitted through a noisy channel, one that may introduce errors in transmission. So before we introduce these codes, we will first describe how Shannon's theory tells us the maximum rate at which information can be transmitted over a noisy channel,
Transmission over a noisy channel
 Let's consider a channel $W$ through which we send a symbol $x$ and receive a symbol $y$. Ideally, we receive the same symbol that we send, or at least, the sent symbol can be uniquely recovered from the received symbol. In practice, however, this is not always the case.
Let's consider a channel $W$ through which we send a symbol $x$ and receive a symbol $y$. Ideally, we receive the same symbol that we send, or at least, the sent symbol can be uniquely recovered from the received symbol. In practice, however, this is not always the case.
For example, the following channel sends symbols from the set $\cx=\{0,1\}$ and receives symbols in $\cy=\{0,1\}$. However, there is a chance that the symbol is corrupted in transmission. In particular, the probability is $p$ that we receive the same symbol we send and $1-p$ that we receive the other symbol. Such a channel is called a binary symmetric channel, which we'll denote as $BSC(p)$.
Our central problem is to understand the maximum rate at which information can be transmitted through such a channel and to find a way to do so that minimizes errors.
To this end, Shannon generalizes the concept of entropy. If $X$ is an information source whose symbols are sent through $W$ and $Y$ is the information source of received symbols, we have joint probabilities $p(x,y)$ that describe the frequency with which we send $x$ and receive $y$. There are also the conditional probabilities $p(y|x)$, the probability that we receive $y$ assuming we have sent $x$, and $p(x|y)$, the probability that we sent $x$ assuming we received $y$. These give conditional entropies $$ \begin{aligned} H(Y|X) = & -\sum_{x,y} p(x,y)\lg p(y|x) \\ H(X|Y) = & -\sum_{x,y} p(x,y)\lg p(x|y). \end{aligned} $$
We are especially interested in $H(X|Y)$, which Shannon calls the channel's equivocation. To understand this better, consider a fixed $y$ and form $$ H(X|y) = -\sum_x p(x|y) \lg p(x|y), $$ which measures our uncertainty in the sent symbol $x$ if we have received $y$. The equivocation is the average of $H(X|y)$ over the received symbols $y$: $$ H(X|Y) = \sum_y p(y) H(X|y). $$ Thinking of entropy as a measure of uncertainty, equivocation measures the uncertainty we have in reconstructing the sent symbols from the received. We can also think of it as the amount of information lost in transmission.
For example, suppose that our channel is $BSC(1)$, which means we are guaranteed that $y=x$, so the received symbol is the same as the transmitted symbol. Then $p(x|y) = 1$ if $y=x$ and $p(x|y) = 0$ otherwise, which leads us to conclude that $H(X|Y) = 0$. In this case, the equivocation is zero, and no information is lost.
On the other hand, working with $BSC(1/2)$, we are as likely to receive a 0 as we are a 1, no matter which symbol is sent. It is therefore impossible to conclude anything about the sent symbol so all the information is lost. A simple calculation shows that the equivocation $H(X|Y) = H(X)$.
The difference $H(X) - H(X|Y)$, which describes the amount of information generated minus the amount lost in transmission, measures the amount of information transmitted by the channel. Shannon therefore defines the capacity of a noisy channel $W$ to be the maximum $$ I(W) = \max_X[H(X) - H(X|Y)] $$ over all information sources using the set of symbols $\cx$.
-
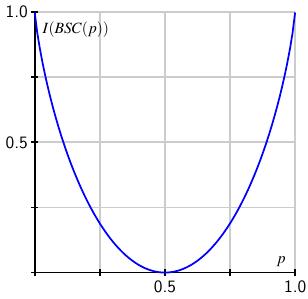
For example, if $W = BSC(1)$, we have $H(X|Y) = 0$ so $$ I(BSC(1)) = \max_X[H(X)] = 1, $$ which happens when the symbols 0 and 1 appear with equal frequency. The capacity of this channel is therefore 1 bit per unit time.
-
However, if $W=BSC(1/2)$, we have $H(X|Y) = H(X)$ so $$ I(BSC(1/2)) = \max_X[H(X) - H(X|Y)] = 0, $$ meaning this channel has zero capacity. No information can be transmitted through it.
The term capacity is motivated by what Shannon calls the Fundamental Theorem of Noisy Channels:
Suppose $X$ is an information source whose entropy is no more than the capacity of a channel $W$; that is, $H(X) \leq I(W)$. Then the symbols of $X$ can be encoded into $\cx$, the input symbols of $W$, so that the source can be transmitted over the channel with an arbitrarily small error rate. If $H(X) \gt I(W)$, there is no such encoding.
This result may initially appear surprising: how can we send information over a noisy channel, a channel that we know can introduce errors, with an arbitrarily small rate of errors? As an example, consider the channel $W$ with inputs and outputs $\cx=\cy=\{a,b,c,d\}$ and whose transmission probabilities are as shown:
Remembering that $I(W) = \max_X[H(X) - H(X|Y)]$, we find with a little work that the maximum occurs when the symbols of $X$ appear equally often so that $H(X) = 2$. It turns out that the equivocation $H(X|Y) = 1$, which implies that the capacity $I(W) = 1$ bit per unit time.
Suppose now that we have the information source whose symbols are $\{0,1\}$, where each symbol occurs with equal frequency. We know that $H(X) = 1$ so Shannon's theorem tells us that we should be able to encode $\{0,1\}$ into $\{a,b,c,d\}$ with an arbitrarily small error rate. In fact, the encoding $$ \begin{aligned} 0 & \to a \\ 1 & \to c \end{aligned} $$ accomplishes this goal. If we receive either $a$ or $b$, we are guaranteed that $0$ was sent; likewise, if we receive either $c$ or $d$, we know that $1$ was sent. It is therefore possible to transmit the information generated by $X$ through $W$ without errors.
This example shows that we can use a noisy channel to send error-free messages by using a subset of the input symbols. Another technique for reducing the error rate is the strategic use of redundancy. As a simple example, suppose our channel is $BSC(0.75)$; sending every symbol three times allows us to reduce the error rate from 25% to about 14%.
Unfortunately, the proof of Shannon's theorem tells us that an encoding with an arbitrarily small error rate exists, but it doesn't provide a means of constructing it. This then is the significance of Arikan's polar codes: they provide encodings for an important class of channels that enable us to transmit information at the greatest possible rate and with an arbitrarily small error rate. As we will see, the strategy for creating these codes is a creative use of redundancy.
Symmetric, binary-input channels
Before describing Arikan's polar codes, let's take a moment to clarify the type of channels $W:\cx\to\cy$ we will be working with. The inputs are $\cx=\{0,1\}$ and we require the channel to be symmetric, which means there is a permutation $\pi:\cy\to\cy$ such that $\pi^{-1} = \pi$ and $p(\pi(y)|1) = p(y|0)$. Such a channel is called a symmetric, binary-input channel. The symmetry condition simply ensures that the result of transmitting 0 is statistically equivalent to transmitting 1.
A typical example is the binary symmetric channel $BSC(p):\{0,1\}\to\{0,1\}$ that we described earlier. The symmetry condition is met with the permutation $\pi$ that simply interchanges 0 and 1.
There are two quantities associated to a symmetric channel $W$ that will be of interest.
-
The first, of course, is the capacity $I(W)$, which measures the rate at which information can be transmitted through the channel. It's not hard to see that the capacity $$ I(W) = \max_X[H(X) - H(X|Y)] $$ is found with the information source $X$ that generates 0 and 1 with equal probability. This means that $p(x) = 1/2$ for both choices of $x$.
Remembering that conditional probabilities are related by $$ p(x|y)p(y) = p(x,y) = p(y|x)p(x), $$ we have $$ \frac{p(x)}{p(x|y)} = \frac{p(y)}{p(y|x)}. $$ This implies that $$ \begin{aligned} -\sum_{x,y} p(x,y) & \lg p(x) + \sum_{x,y}p(x,y)\lg p(x|y) = \\ & -\sum_{x,y} p(x,y) \lg p(y) + \sum_{x,y}p(x,y)\lg p(y|x) \\ \end{aligned} $$ and so $$ H(X) - H(X|Y) = H(Y) - H(Y|X). $$
Since $p(x) = \frac12$, we also have that $p(y) = \frac12 p(y|0) + \frac12 p(y|1)$ and $p(x,y) = \frac12 p(y|x)$. This finally leads to the expression $$ I(W) = \sum_{x,y} \frac12 p(y|x) \lg \frac{p(y|x)}{\frac12 p(y|0) + \frac12p(y|1)}. $$ This is a particularly convenient form for computing the capacity since it is expressed only in terms of the conditional probabilities $p(y|x)$.
In particular, for the binary symmetric channel, we find $$ I(BSC(p)) = 1-H(p) = 1-p\lg(p) - (1-p)\lg(1-p), $$ reinforcing our earlier observation that $H(p)$ is a measure of the information lost in the noisy channel.
Since the capacity of a symmetric, binary input channel is computed as $\max_X[H(X) - H(X|Y)]$ where $H(X) \leq 1$, it follows that $0\leq I(W) \leq 1$. When $I(W) = 1$, the equivocation $H(Y|X) = 0$ so no information is lost and this is a perfect channel. In the example above, this happens when $p=0$ or $1$.
At the other extreme, a channel for which $I(W) = 0$ is useless since no information is transmitted.
-
A second quantity associated to a symmetric channel $W$ measures the reliability with which symbols are transmitted. Given a received symbol $y$, we can consider the product $$ p(y|0)~p(y|1) $$ as a reflection of the confidence we have in deducing the sent symbol when $y$ is received. For instance, if this product is 0, one of the conditional probabilities is zero, which means we know the sent symbol when we receive $y$.
We therefore define the Bhattacharyya parameter $$ Z(W) = \sum_y \sqrt{p(y|0)~p(y|1)} $$ as a measure of the channel's reliability. It turns out that $0\leq Z(W)\leq 1$, and lower values of $Z(W)$ indicate greater reliability. For instance, when $Z(W) = 0$, then every product $p(y|0)~p(y|1) = 0$, which means the symbols are transmitted without error.
We expect $Z(W)$, the channel's reliability, to be related to $I(W)$, the rate of transmission. Indeed, Arikan shows that $Z(W)\approx 0$ means that $I(W)\approx 1$ and that $Z(W)\approx 1$ means that $I(W)\approx 0$. So a high-quality channel will have $I\approx 1$ and $Z\approx 0$, and a poor channel will have $I\approx 0$ and $Z\approx 1$.
For the binary symmetric channel $BSC(p)$, we see the following relationship:
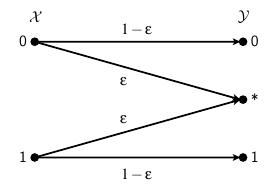
Besides the binary symmetric channel, another example of a symmetric, binary-input channel is the binary erasure channel $W:\{0,1\}\to\{0,*,1\}$ as shown below. We think of the received symbol $*$ as an erasure, meaning the symbol was received yet we do not know what it is, so $\ep$ represents the probability that a sent symbol is erased.
Once again, the permutation $\pi$ that interchanges 0 and 1 while fixing $*$ confirms this as a symmetric channel that we denote as $BEC(\ep)$. The diagram gives the conditional probabilities that we need to find the capacity and Bhattacharyya parameter $$ \begin{aligned} I(BEC(\ep)) & = 1-\ep \\ Z(BEC(\ep)) & = \ep. \end{aligned} $$ Notice that if $\ep=0$, there is no possibility of an erasure and the capacity $I(BEC(0)) = 1$ bit per unit time. On the other hand, if $\ep=1$, every symbol is erased so we have $I(BEC(1)) = 0$ telling us this channel can transmit no information.
Polarization: A first step
 Polar codes are constructed through a recursive process, the first step of which we'll now describe. Beginning with a channel $W$, we'll bundle together two copies of $W$ into a vector channel $W_2:\cx^2\to\cy^2$. Then we'll pull the vector channel apart into two symmetric, binary-input channels $\chan{1}{2}$ and $\chan{2}{2}$ and observe how the capacity of these two channels is distributed.
Polar codes are constructed through a recursive process, the first step of which we'll now describe. Beginning with a channel $W$, we'll bundle together two copies of $W$ into a vector channel $W_2:\cx^2\to\cy^2$. Then we'll pull the vector channel apart into two symmetric, binary-input channels $\chan{1}{2}$ and $\chan{2}{2}$ and observe how the capacity of these two channels is distributed.
In what follows, we will be considering a number of different channels. We will therefore denote the conditional probabilities of a particular channel using the same symbol as the channel. For instance, if $W=BEC(\ep)$, we will write, say, the conditional probability $W(*|1)=\ep$.
Our vector channel $W_2:\cx^2\to\cy^2$ begins with a two-dimensional input $(u_1,u_2)$ and forms $(x_1,x_2) = (u_1\oplus u_2, u_2)$, where $\oplus$ denotes integer addition modulo 2. Then $x_1$ and $x_2$ are transmitted through $W$, as shown below.
This gives the transmission probabilities $$ W_2((y_1,y_2) | (u_1,u_2)) = W(y_1|u_1\oplus u_2)W(y_2|u_2). $$ It is fairly straightforward to see that $I(W_2) = 2I(W)$ so that we have not lost any capacity.
From here, we obtain two channels: $$ \begin{aligned} \chan{1}{2}&: \cx\to\cy^2 \\ \chan{2}{2}&: \cx\to\cy^2\times \cx. \end{aligned} $$ whose transition probabilities are defined by $$ \begin{aligned} \chan{1}{2}((y_1,y_2)|u_1) & = \frac12 \left(W_2((y_1,y_2)|(u_1,0)) + W_2((y_1,y_2)|(u_1,1))\right) \\ \chan{2}{2}(((y_1,y_2),u_1)|u_2) & = \frac12 W_2((y_1,y_2)|(u_1,u_2)). \end{aligned} $$ This may look a little daunting, but we'll soon look at an example illustrating how this works.
The important point is that we can verify that the total capacity is preserved, $$ I(\chan{1}{2})+I(\chan{2}{2}) = I(W_2) = 2I(W), $$ and redistributed advantageously $$ I(\chan{1}{2})\leq I(W) \leq I(\chan{2}{2}). $$ That is, $\chan{1}{2}$ surrenders some of its capacity to $\chan{2}{2}$, pushing $\chan{1}{2}$ toward a useless channel and $\chan{2}{2}$ toward a perfect channel.
Let's consider what happens when our channel is a binary erasure channel $BEC(\ep)$.
Working out the transition probabilities for $\chan{1}{2}$, we have $$ \begin{array}{c||c|c} (y_1,y_2) \backslash x & 0 & 1 \\ \hline (0,0) & \frac12(1-\ep)^2 & 0 \\ (0,1) & 0 & \frac12(1-\ep)^2 \\ (0,*) & \frac12(1-\ep)\ep & \frac12(1-\ep)\ep \\ (1,0) & 0 & \frac12(1-\ep)^2 \\ (1,1) & \frac12(1-\ep)^2 & 0 \\ (1,*) & \frac12(1-\ep)\ep & \frac12(1-\ep)\ep \\ (*,0) & \frac12(1-\ep)\ep & \frac12(1-\ep)\ep \\ (*,1) & \frac12(1-\ep)\ep & \frac12(1-\ep)\ep \\ (*,*) & \ep^2 & \ep^2 \\ \end{array} $$ Rather than focusing on the individual probabilities, notice that five of the nine received symbols satisfy $\chan{1}{2}(y|0)~\chan{1}{2}(y|1) \neq 0$. More specifically, if either $y_1=*$ or $y_2=*$, it is equally likely that 0 or 1 was sent.
This observation is reflected in the fact that the capacity and reliability have both decreased. More specifically, we have $$ \begin{aligned} I(\chan{1}{2}) = (1-\ep)^2 & \leq (1-\ep) = I(W) \\ Z(\chan{1}{2}) = 2\ep-\ep^2 & \geq \ep = Z(W), \\ \end{aligned} $$ where we recall that larger values of the Bhattacharyya parameter indicate less reliability.
Let's compare this to the second channel $\chan{2}{2}$. The received symbols are now $\cy^2\times \cx$. If we work out the conditional probabilities for half of them, the ones having the form $((y_1,y_2),0)$, we find $$ \begin{array}{c||c|c} ((y_1,y_2),0) \backslash x & 0 & 1 \\ \hline ((0,0),0) & \frac12(1-\ep)^2 & 0 \\ ((0,1),0) & 0 & 0 \\ ((0,*),0) & \frac12(1-\ep)\ep & 0 \\ ((1,0),0) & 0 & \frac12(1-\ep)^2 \\ ((1,1),0) & 0 & 0 \\ ((1,*),0) & 0 & \frac12(1-\ep)\ep \\ ((*,0),0) & \frac12(1-\ep)\ep & 0 \\ ((*,1),0) & 0 & \frac12(1-\ep)\ep \\ ((*,*),0) & \frac12\ep^2 & \frac12\ep^2 \\ \end{array} $$ This channel behaves much differently. For all but one received symbol, we can uniquely determine the sent symbol $x$. In particular, we can recover the sent symbol even if one of the received symbols has been erased. This leads to an increase in the capacity and a decrease in the Bhattacharyya parameter: $$ \begin{aligned} I(\chan{2}{2}) = 1-\ep^2 & \geq 1-\ep = I(W) \\ Z(\chan{2}{2}) = \ep^2 & \leq \ep = Z(W). \\ \end{aligned} $$
The capacities of these channels, as a function of $\epsilon$, are shown below.
It's worth thinking about why the second channel $\chan{2}{2}$ performs better than the original. While the vector channel $W_2:\cx^2\to\cy^2$ transmits the pair $(u_1,u_2)$, $\chan{2}{2}$ assumes that $u_1$ is transmitted without error so that the received symbol is $((y_1,y_2), u_1)$. Since we know $u_1$ arrives safely, we are essentially transmitting $u_2$ through $W$ twice. It is this redundancy that causes the capacity and reliability to both improve. In practice, we will need to deal with our assumption that $u_1$ is transmitted correctly, but we'll worry about that later.
If we had instead considered a binary symmetric channel $W = BSC(p)$, we find a similar picture:
Polarization: The recursive step
We have now taken the first step in the polarization process: We started with two copies of $W$ and created two new polarized channels, one with improved capacity, the other with diminished capacity. Next, we will repeat this step recursively so as to create new channels, some of which approach perfect channels and some of which approach useless channels.
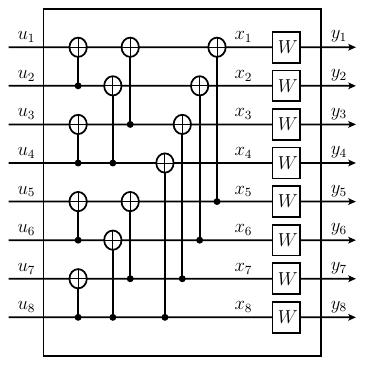
When $N$ is a power of 2, we form the vector channel $W_{N}:\cx^{N}\to\cy^{N}$ from two copies of $W_{N/2}$. The recipe to create $W_4$ from two copies of $W_2$ is shown below.
From the inputs $(u_1, u_2, \ldots, u_{N})$, we form $(s_1,\ldots, s_{N})$ as $s_{2i-1} = u_{2i-1}\oplus u_{2i}$ and $s_{2i} = u_{2i}$. We then use a reverse shuffle permutation to form $$ (v_1,v_2,\ldots,v_{N}) = (s_1, s_3, \ldots, s_{N-1}, s_2, s_4,\ldots, s_{N}), $$ which serve as the inputs for two copies of $W_{N/2}$.
While that may sound a little complicated, the representation of $W_8$ shown below illustrates the underlying simplicity.
We now form new symmetric, binary-input channels $$ \chan{i}{N}:\cx\to \cy^N\times \cx^{i-1} $$ as we did before: $$ \begin{aligned} \chan{i}{N}(((y_1,\ldots,y_N),& (u_1,\ldots,u_{i-1}))~|~u_i) = \\ & \frac1{2^{N-1}}\sum_{(u_{i+1},\ldots,u_N)} W_N((y_1,\ldots,y_N)|(u_1,\ldots,u_N)). \end{aligned} $$
Arikan then proves a remarkable result:
If we choose $\delta\in(0,1)$, then as $N$ grows through powers of two, the fraction of channels satisfying $I(\chan{i}{N}) \in (1-\delta, 1]$ approaches $I(W)$. Likewise, the fraction of channels with $I(\chan{i}{N}) \in [0,\delta)$ approaches $1-I(W)$.
Suppose, for instance, that we begin with a channel whose capacity $I(W) = 0.75$. As we repeat the recursive step, we find that close to 75% of the channels are nearly perfect and close to 25% are nearly useless.
More specifically, with the binary erasure channel $BEC(0.25)$, whose capacity is 0.75, and $N=1024$, the channel capacities are as shown below. About three-quarters of the channels are close to perfect and about one-quarter are close to useless.
For comparison, here's the result with $BEC(0.75)$, whose capacity is 0.25.
It should be no surprise that the channels $\chan{i}{N}$ with small $i$ are close to useless while the ones with large $i$ are close to perfect. Remember that $\chan{i}{N}$ assumes that the symbols $(u_1,\ldots,u_{i-1})$ are transmitted without error. When $i$ is large, we know that many of the symbols are reliably transmitted so the channel transmits $u_i$ with a lot of redundancy. This redundancy causes an increase in channel capacity $I(\chan{i}{N})$ and a corresponding decrease in our reliability measure $Z(\chan{i}{N})$.
Encoding and decoding
Now that we have a large number of nearly perfect channels, we can describe how data is encoded and decoded to enable transmission through them. For some large value of $N$, we have approximately $NI(W)$ nearly perfect channels and $N-NI(W)$ nearly useless channels. Our goal is to funnel all the data through the nearly perfect channels and ignore the others.
To illustrate, consider the channel $W = BEC(0.5)$ with $I(W) = 0.5$, and suppose we have created $N=8$ channels. This is a relatively small value of $N$, but we expect $NI(W) = 4$ nearly perfect channels and $N-NI(W)=4$ nearly useless channels. The capacity of the 8 channels is as shown here.
We will choose channels 4, 6, 7, and 8 to transmit data. To do so, we will fix values for $u_1$, $u_2$, $u_3$, and $u_5$ and declare these to be "frozen" (these are polar codes, after all). Arikan shows that any choice for the frozen bits works equally well; this shouldn't be too surprising since their corresponding channels transmit hardly any information. The other symbols $u_4$, $u_6$, $u_7$, and $u_8$ will contain data we wish to transmit.
Encoding the data means evaluating the $x_i$ in terms of the $u_j$. As seen in the figure, we perform $N/2=4$ additions $\lg(N) = 3$ times, which illustrates why the complexity of the encoding operation is $O(N\log N)$.
Now we come to the problem of decoding: if we know ${\mathbf y} = (y_1,\ldots, y_N)$, how do we recover ${\mathbf u} = (u_1,\ldots, u_N)$? We decode ${\mathbf y}$ into the vector $\hat{\mathbf u} = (\hat{u}_1,\ldots,\hat{u}_N)$ working from left to right.
First, we declare $\hat{u}_i = u_i$ if $u_i$ is frozen. Once we have found $(\hu_1, \ldots, \hu_{i-1})$, we define the ratio of conditional probabilities $$ h_i = \frac{\chan{i}{N}(({\mathbf y}, (\hu_1,\ldots,\hu_{i-1}))|0)} {\chan{i}{N}(({\mathbf y}, (\hu_1,\ldots,\hu_{i-1}))|1)}. $$ If $h_i \geq 1$, then $u_i$ is more likely to be 0 than 1 so we define $$ \hu_i = \begin{cases} 0 & \mbox{if}~ h_i \geq 1 \\ 1 & \mbox{else.} \end{cases} $$
Two observations are important. First, suppose we begin with ${\mathbf u}=(u_1,\ldots,u_N)$ and arrive at $\hat{\mathbf u} = (\hu_1,\ldots,\hu_N)$ after the decoding process. If $\hat{\mathbf u} \neq {\mathbf u}$, we say that a block error has occurred. Arikan shows that, as long as the fraction of non-frozen channels is less than $I(W)$, then the probability of a block error approaches 0 as $N$ grows. This makes sense intuitively: the channels $\chan{i}{N}$ we are using to transmit data are nearly perfect, which means that $Z(\chan{i}{N})\approx 0$. In other words, these channels are highly reliable so the frequency of errors will be relatively small.
Second, Arikan demonstrates a recursive technique for finding the conditional probabilities $\chan{i}{N}$ in terms of $\chan{j}{N/2}$, which means we can evaluate $h_i$ with complexity $O(\log N)$. Therefore, the complexity of the decoding operation is $O(N\log N)$, matching the complexity of the encoding operation.
The complexity of the encoding and decoding operations means that they can be practically implemented. So now we find ourselves with a practical means to transmit data at capacity $I(W)$ and with an arbitrarily small error rate. We have therefore constructed an encoding that is optimal according to the Fundamental Theorem of Noisy Channels.
Summary
Arikan's introduction of polar codes motivated a great deal of further work that brought the theory to a point where it could be usefully implemented within the new 5G standard. One obstacle to overcome was that of simply constructing the codes by determining which channels should be frozen and which should transmit data.
In our example above, we considered a specific channel, a binary erasure channel $W = BSC(\ep)$, for which it is relatively easy to explicitly compute the capacity and reliability of the polarized channels $\chan{i}{N}$. This is an exception, however, as there is not an efficient method for finding these measures for a general channel $W$. Fortunately, later work by Tal and Vardy provided techniques to estimate the reliability of the polarized channels in an efficient way.
Additional effort went into improving the decoding operation, which was, in practice, too slow and error prone to be effective. With this hurdle overcome, polar codes have now been adopted into the 5G framework, only 10 years after their original introduction.
References


 David Austin
David Austin 
 Let's consider a channel $W$ through which we send a symbol $x$ and receive a symbol $y$. Ideally, we receive the same symbol that we send, or at least, the sent symbol can be uniquely recovered from the received symbol. In practice, however, this is not always the case.
Let's consider a channel $W$ through which we send a symbol $x$ and receive a symbol $y$. Ideally, we receive the same symbol that we send, or at least, the sent symbol can be uniquely recovered from the received symbol. In practice, however, this is not always the case.