The methods below go under a surprisingly large number of names, partly because the methods were independently discovered for a variety of reasons. Here is a table of equivalency for these names.

Hamilton's Method

Hamilton's method (for AP) conceptually starts by relaxing the requirement that the number of seats assigned to each state be an integer and looking at what the exact quota that each state is entitled to would be. This exact quota q_i for state i can be computed by either of two calculations, each of which gives one a slightly different perspective. In the first instance, we can think of state i's share as the percent of the population state i has times the number of seats available. In the second instance one computes the number of people per seat (P/h) (i.e. the size of an ideal district) and divides this into the population of state i, to see its share


 

One can think of q_i as consisting of an integer part plus a fractional part. This integer part is referred to as lower quota, since intuitively each state should get at least this number of seats, and one more than this integer part is referred to as upper quota. Hamilton's method for the AP problem works by giving each state its lower quota. If there are any seats that have not been distributed, these are given out in the order of largest remainder, that is, in order of the size of the fractional parts. Obviously, there is a need for tie-breaking rules in the case that states have equal population. However, both with Hamilton's method and other methods we will discuss later, ties can result from other circumstances than equality of population. (Of course, in the case of CAP, the large numbers involved reduce the chance of such ties. Also, for the CAP problem, the discussion above must be modified so that the requirement that each state get one or more seats be dealt with.) Hamilton's method has a very appealing property. Each state gets either its lower quota or upper quota, that is, the number of seats that a state gets in the House of Representatives is either the largest integer less than or equal to a states' quota q_i or one more than this number. Yet, as mentioned in the historical section Hamilton's method can fail, using a fixed set of populations, to guarantee that as the house size goes up, a state will not lose(!) a seat. Thus, Hamilton's method violates the sensible requirement, for some AP problems, of house size monotonicity.

Example 1:
 

The table above shows the results of two consecutive censuses where there are three regions and 100 seats to distribute to the three states in a regional legislature. Note that the population of A has gone up and the population of B has gone up, while the population of C has gone down between the two censuses.

Let us apply Hamilton's method to these two data sets. For the first data set, the total population is 1,000,000, so the exact quota values of A, B, and C are 65.7, 23.7, and 10.6, respectively. Assigning each state its lower quota gives A
65 seats, B 23 seats, and C 10 seats. These number a total of 98, so the two remaining seats are given to the two states with the largest fractional parts, A and B. The final result is that A gets 66 seats, B gets 24 seats, and C gets 10 seats. In the later census, the total population has risen to 1,010,000. A, B, and C's exact quotas are now 65.346, 24.267, and 10.386. Now initially, A gets 65 seats, B gets 24 seats, and C gets 10 seats for a total of 99. The one remaining seat is assigned to C because its fractional part is largest. The result is that A gets 65 seats, B gets 24 seats, while C gets 11 seats. Thus, although A and B's populations went up and C's went down, A's number of seats went down, B's stayed the same, and C's went up. Note also what happens for the second census data if it was decided to distribute 101 seats instead of 100 seats. The exact quota for A, B, and C would become: 66.00, 24.51, and 10.49, respectively. Thus, initially A would get 66 seats, B would get 24 seats, and C would get 10 seats. Since only 100 seats have been distributed, one more seat would go to B, which has the largest remainder. Thus, A gets 66 seats, B gets 25 seats and C gets 10 seats. As a result, C gets fewer seats in a larger house! This example illustrates that Hamilton's method allows the population paradox and the Alabama paradox.

Other Methods

The next example will examine a very different approach to dealing with the fractional parts of exact quotas when trying to get a reasonable apportionment.

Example 2:

 

We will suppose that we have 10 seats to distribute and note that the total population of all the states is 1100.

We will illustrate Webster's method of apportionment by using the data in this example. We can begin by computing the exact quota that each state is entitled to:
 

In grade school you probably learned how to round decimal numbers to the nearest integer. This procedure required that if the fractional part were .5 or more, one rounded up to the next largest integer; if the fractional part was smaller than .5, then you rounded down. If we apply this approach to the numbers in the example above we would give 6 seats to A, 3 seats to B, and 1 seat to C. Since these numbers add to 10, we can use these values to apportion the 10 seats.

However, we were lucky in this case. The rounding distributed exactly 10 seats. This will not always happen. We might wind up distributing fewer than h seats or more than h seats if we use the usual rounding rule. To illustrate what to do in these other situations we will consider the example below. Note how little the numbers have been changed from Example 2.


Example 3:
 

Again we will suppose that we have 10 seats to distribute and note that the total population of all the states is 1100. Since there are 1100 people and 10 seats to distribute, ideally we would like to be able to have one district for every 110 people (i.e. 1100/10). This number 110 is known as the ideal district size. Notice that it usually will not be an integer, but we allow this. Using this ideal district size we can compute each state's exact quota.
 

Using the grade school approach to rounding we would give 6 seats to A, 2 seats to B, and 1 seat to C, which adds up to only 9 seats, one short of the 10 we must distribute. The Webster method approach to handling this problem is that one can modify the ideal district size to obtain a modified district size (MDS). By dividing the state populations by the MDS one gets modified quotas which hopefully, when rounded in the usual way, will distribute h seats. Since in our example we distributed too few seats, we must use a smaller MDS, which will increase the size of the fractional parts, so when we round them we distribute more seats (but not too many). We will use a MDS of 107.2. (Can you figure out from the calculation below why that value was chosen?) Generally there will be an interval of numbers which if we use any number in this range as an MDS, will distribute the desired h seats.)

Computing modified quotas based on the MDS gives:
 

When we round we give 6 seats to A, 3 seats to B and 1 seat to C, which adds up to 10 seats, the number we need to distribute.

Having seen this approach to apportioning seats, it is very natural to realize that one will get other methods by choosing a different rounding rule than the usual one! In fact, the other methods which were described in the history section can be thought of as working in exactly this way.

Jefferson's method is based on taking the fractional part of the exact quota or modified quota and always rounding it down, no matter how small the fractional part may be. Adams' method is based on taking the fractional part of the exact quota or modified exact quota and always rounding it up, no matter how small the fractional part may be. If the result does not apportion the correct number of seats h, one changes the MDS up or down so as to apportion exactly h seats.

Example 3 (continued)

If we apply Jefferson's method to the exact quotas, we round all the fractions down so we give 6 seats to A, 2 seats to B, and 1 seat to C. This distributes too few seats, only 9 of the 10 we need to distribute. If we use a MDS of 98 and compute modified quotas, we get:
 

Rounding all the fractions down gives the assignment of 7 seats to A, 2 seats to B, and 1 seat to C, which gives the desired total of 10.

If we apply Adams' method to the exact quotas, we round all the fractions up so we give 7 seats to A, 3 seats to B, and 2 seat to C. This distributes too many seats, 12 seats instead of the 10 we need to distribute. If we use a MDS of 135 and computed modified quotas we get:
 

Rounding all the fractions down gives the assignment of 6 seats to A, 2 seats to B, and 2 seats to C, which gives the desired total of 10.

The three methods we have used have given rather different results, as summarized in the chart below:

 

Note that in this example all three methods give each state either its lower or upper quota. However, it is important to realize that this is not true of all examples. Furthermore the method used to apportion the United States House of Representatives (described below) need not obey this fairness rule.

Even this very oversimplified setting suggests that Jefferson's method and Adams' method have extreme behavior, the former tending to overly reward large states and the latter tending to overly reward small states.

The two other historical methods due to Dean and Huntington can also be described in terms of rounding rules. Dean's method is based on the harmonic mean of two numbers and Huntington's is based on the geometric mean of the two numbers. (One can think of Webster's method as being based on the familiar arithmetical mean.) Here is a way of describing these two methods. Suppose we want to decide whether to round the exact quota or modified quota q up or down. For Dean's method one rounds up if q is greater than or equal to the harmonic mean of q and q +1, otherwise one rounds down, while for Huntington's method (the method currently used in the United States to apportion our House of Representatives) one rounds up if q is greater than or equal to the geometric mean of q and q + 1 (e.g.q(q+1)), while otherwise one rounds down. Recall that the harmonic mean of x and y is given by 2xy/(x +y), while the geometric mean of x and y is given by (xy). For our purposes the important thing is that the harmonic mean and geometric mean of q and q + 1 are numbers between q and q +1. The situations in which different means arise is an interesting subject in its own right which will not be explored here.

The five methods we have looked at, Adams, Dean, Huntington-Hill, Jefferson, and Webster were introduced here as based on different rounding rules. They are usually referred to as divisor methods because they are based on dividing a state's population by either an ideal district size or a MDS, and then rounding. However, it is remarkable that there is a different way of thinking of these five methods that is of interest both for computing apportionments and for thinking about the properties of these methods. This accomplishment was carried out by E. V. Huntington. The point of view is the following. Suppose that instead of thinking of the h seats which are to be distributed as being distributed all at once, imagine that they are being given away one at a time until we reach h. In this dynamical setting, we give the seats away until they are all gone. The idea is that one can prepare in advance a priority table of numbers for each of the five historical methods. This table is used to assign seats to states one after another in a remarkably simple way: give the first seat to the state with the largest number in the table, the second seat to the state with the next largest, etc. This approach is often referred to as the ranking function, but I will use the language of priority tables instead. The way to prepare the table for each of the five methods works in this way.

Using the formula associated with the method, the ith row of the table (i = 1, 2, ....) is obtained by dividing the populations of the states by substituting (i-1) for the value of a in the formula. Thus, for the 4th row (i = 4) in the Huntington-Hill method divide the populations by ((3(3+1)) = (12) and enter the result in the 4th row. If substitution of 0 in the formula involves division by zero, we indicate this by writing the infinity symbol in the table. This will be shorthand for saying that this method automatically gives each state one seat. (Methods which do not have the infinity symbol in the top row must be modified for use in the CAP problem, because they will not automatically meet the constitutional provision of giving each state at least one seat.) The formulas to construct a priority table are:

 

Adams	a (rows obtained by dividing by 0,1 and 2,...)
Dean	2a (a + 1) / (2a +1)
Huntington-Hill
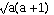
Webster	(2a + 1) / 2
Jefferson	a + 1

Example 3 (continued)
 

	A	B	C
	696	268	136
1
2	696	268	136
3	348	134	72
4	232	89.3	45.3
5	174	67	34
6	139.2	53.6	27.2
7	116	44.7	22.7

The table above indicates the priority numbers for the Adams method. In the first row we divided by 0, in the second row by 1, in the third row by 2, etc.

Since the first row has the symbol infinity, we give each state one seat. Who gets the 4th seat? A, because the largest number not used from the table is 696 in row 1, column A; the 5th seat goes to A as well because there is a 348 in row 2, column A; the 6th seat goes to B (priority number 268); the 7th seat to A (priority number 232); the 8th seat to A (priority number 174), the 9th seat goes to A (priority number 139.2) and the 10th seat to C (priority number 136). You can check this yields 6 seats for A, 2 seats for B, and 2 seats for C as before (using MDS approach.)

For Webster's method the rows are divided by 1/2, 3/2, 5/2, etc. However, since the seats are assigned by order of size, one can divide the rows by 1, 3, 5, ... instead, since this gives the same size order for the numbers in the table.
 

1. Apportionment Systems
2. Fairness and Apportionment
3. Balinski and Young's Contribution
4. Where to Next?
5. References