Strange Associations
Posted November 2007.
There are many other polytopes that can be described in purely combinatorial terms. Among the more curious are the associahedra....
Bill Casselman
University of British Columbia, Vancouver, Canada
cass at math.ubc.ca
Introduction
A polytope of n dimensions is the convex hull of a finite collection of points in an n-dimensional vector space Rn that is non-degenerate in the sense that it does not lie in some subspace of n-1 dimensions. "Convex" here means, roughly, that the shape bulges out. "Hull" means that the actual corners, or vertices, of the figure are among the original set of points. In two dimensions, polytopes are just polygons, such as this hexagon:

In three dimensions they are polyhedra, such as these familiar ones:





There is a vast theory of such geometrical objects. The most interesting ones are those with some important connection to branches of mathematics other than geometry, for example bringing to light situations where geometry says something about algebraic structures. In this note, I'll say something about the polytopes known as associahedra, and try to say something about their algebraic significance as well.
There is exactly one associahedron of each dimension. It is labeled by an index n+2. Thus K5 looks like this:

This is not at first sight a lovable figure, not elegantly symmetrical like the more familiar regular polyhedra, and indeed to all appearances assembled rather randomly. But then true beauty is never based on superficial appearances, is it?
Simplices
I'll start with the ... well, simplest ... examples of polytopes. They are called simplices (singular: simplex). Suppose we are given in Rn(n-dimensional space) a collection of n+1 points that do not lie in n-1 dimensions. For example, in R2 we would be given three non-collinear points A, B, C; and in three dimensions four points, not lying in a plane. The simplex determined by them is their convex hull. In two dimensions this is a triangle
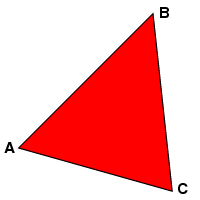
and in 3 dimensions a tetrahedron.
The faces of any polytope are ... well, its faces - the flat subsets making up its boundary. They come in different dimensions. The vertices are its extremal points, its edges are the links between neighbouring vertices, and so on. For a simplex, the faces are simplices of lower dimension, parametrized precisely by the subsets of its vertices (all of them but the empty set, and sometimes it is thrown into the collection as well). In two dimensions the faces of triangle ABC are thus
vertices: A, B, C
edges: AB, AC, BC
the triangle itself: ABC
For a tetrahedron associated to ABCD they are
vertices: A, B, C, D
edges: AB, AC, AD, BC, BD, CD
the two-dimensional triangular faces: ABC, ABD, ACD, BCD
the tetrahedron itself: ABCD
The faces of any polytope make up a set with an order relation: One face is considered to be less than another when it is properly contained in it. For simplices, one face is less than another when its parametrizing subset is contained in that of the other. Thus the edge AB of the tetrahedron ABCD is contained in both the faces ABC and ABD, and no other proper faces. This set and this order are the most important feature of a polytope, rather than the explicit geometric object realizing it. Thus in two dimensions all triangles are essentially the same polytope; in three dimensions all tetrahedra are essentially equivalent; and in general all n-dimensional simplices are essentially the same. Simplices are, in fact, somewhat dull objects. Too ... uh ... simple to be interesting. (But although a single simplex is not so exciting, several simplices assembled together may very well be fascinating. Just as the relatively simple single cells of a multi-celled organism become much more interesting in the assembly.)
Exercise. The convex hull in Rn of all points (xi) with xi = +1 or -1 is an n-dimensional cube. It has 2n vertices. Describe explicitly all of its faces at least when n=2, 3, or 4. How many are there of each dimension for a general n?
The face graph of a polytope
The essential nature of a polytope lies somewhere in between its metric structure and its topological structure. We don't care about the exact size of things. All tetrahedra are equivalent in this business, but we do want to distinguish between a tetrahedron and a cube, even though they have the same topological structure (since both can be smoothly deformed into a sphere). This combinatorial structure is pretty much captured by the face graph of the polytope that displays the set-plus-order I have mentioned above, and does this so that all faces of the same dimension are somehow seen to be of that dimension. This I'll call a ranked graph - that is to say, each node of the graph is assigned a rank (here, the dimension of the face) and if one node is less than another than it has lower rank. Here is the face graph of the triangle ABC:

One very general question considered in this theory is, How can one tell whether a given ranked graph is the face graph of a polytope? This can be a very, very difficult question, even for a particular graph.
Associahedra
The essential nature of the simplex lies in its face graph, but this can be described in purely combinatorial terms - i. e. purely in terms of the subsets of its set of vertices, and the way they are contained in one another. There are many other polytopes that can be described in purely combinatorial terms. Among the more curious are the associahedra. I describe first the combinatorial object.
Start with a product xx ... x of n copies of a single variable x. List what you get when you start inserting balanced parentheses into it, subject to two exclusions: (a) you do not put parentheses (...) around the whole thing and (b) you do not put parentheses around just a single variable. Thus x(x)x and (xxx) are not allowed. If n=4, you start with xxxx. Inserting just one pair you get
(xx)xx
(xxx)x
x(xxx)
xx(xx)
x(xx)x
Inserting two pairs you get
(xx)(xx)
((xx)x)x
(x(xx))x
x(x(xx))
x((xx)x)
You can't insert any more, according to the rules.
At first it might seem that this is a largely messy process. But now I associate to these lists its face graph. At its top is xxxx. This is linked to each one of the expressions with just one pair of parentheses. And one of these expressions is linked to any one of the expressions with two pairs if the one with two pairs is obtained by adding a suitable pair to the first. For example, x(xx)x is linked to (x(xx))x and also x((xx)x). The graph we finally get is this one:
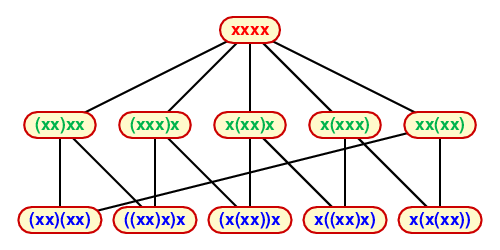
which can be rearranged to look like this:

Thus, we see that the associahedron K4 is a pentagon (vertices blue, edges green). Not too exciting. What about K5? It will be a three-dimensional solid. We start with xxxxx to represent the entire solid. Adding a single pair of balanced parentheses we get
(xx)xxx
(xxx)xx
(xxxx)x
x(xx)xx
x(xxx)x
x(xxxx)
xx(xx)x
xx(xxx)
xxx(xx)
(There is a systematic way to make this list - list first all expressions where the ( occurs at the far left, then where it occurs between the first and second characters, etc.) These parametrize the two-dimensional faces of K5. Next one could list the edges, and finally the vertices. I won't make those lists, but I will tell you that there are 14 vertices, that you can tell how many edges there are by keeping in mind that any edge lies on exactly two 2D (two-dimensional) faces, and that each edge has two vertices as its end points. If you have made a list of all vertices, it is an interesting exercise to figure out how to assemble them into faces. As the first image of K5 shows, among the 2D faces there are three quadrilaterals, and the rest are pentagons.
Rendering
Even when one knows that a given combinatorial structure comes from a polytope, it is not necessarily a trivial matter to construct it explicitly. This is certainly true of associahedra. The very first description of an associahedron is to be found in the Ph. D. thesis of the topologist Jim Stasheff, but he was unable to represent it as a strict polytope. Instead, he had to be content with a somewhat curvy shape. Here is his K5:

Of course, it is easy to see how to modify this to be a true polytope. In fact, John Milnor showed up at Stasheff's thesis defense with a cardboard model. But is is not at all easy to see how to straighten out Stasheff's curvy associahedron in all dimensions.
There are by now many, many constructions of the associahedron as a true polytope. Nearly all of them are intimately related to some deep theoretical understanding of the structure, but ultimately there is some more or less arbitrary decision to be made. This is what one expects, since after all the "essence" of the shape is not, as I have said, in its explicit metric structure.
What seems to be the the simplest rendering in all dimensions is that of Loday. He sets this up in terms of a natural tree structure associated to a well-balanced expression, but I'll describe it in ternms of the expression itself. It works by mathematical induction on the length of the expression.
- First of all, we write our expressions with indexed variables xi, increasing from 0 left to right. So a typical expression might look like (x0(x1x2))x3.
- Any saturated expression can be expressed as a product of two such expressions of lower degree. Thus x0(x1x2) is the product of x0 and x1x2.
- These left and right factors may in general themselves be factored. There will be some expression in the final collection of compound sub-expressions with an xi-1 at the far right end of its left half and xi at the far left of its right half. We label this expression as ei. For example, in the expression (x0(x1x2))(x3x4) we have
e1 = x0(x1x2)
e2 = x1x2
e3 = (x0(x1x2))(x3x4)
e4 = x3x4
- We set ai equal to the degree of the left factor of ei, bi equal to that of its right half. Thus
a1 = 1, b1 = 2
a2 = 1, b2 = 1
a3 = 3, b3 = 2
a4 = 1, b4 = 1
- To the total expression e of degree n we associate the point M(e)an n-1-dimensional point whose coordinates are the products aibi. The expression above thus gives us (2, 1, 6, 1).
Here is Loday's very pretty result:
Theorem. The associahedron of dimension n may be realized in n+1 dimensions as that polytope whose vertices are the points M(e) as e varies over all saturated, balanced expressions of degree n+2.
For n=3 we get the vertices (in compressed format) 1261 1621 1612 2161 1234 1414 2134 4141 3124 4123 4321 4312 4213 3214. These all lie in the 3D hyperplane x0+x1+x2+x3=10, which can be rendered in ordinary 3D. You can see in Loday's paper how these assemble to make the associahedron K5:
(Hidden edges are in red.)
History
The history of associahedra is curious. They were first constructed by the topologist Jim Stasheff in his 1961 Princeton University thesis, where they were used to explore various kinds of topological associativity. Stasheff tells me that his thesis was received with no fanfare, and that in fact he had some trouble getting his research published. It was turned down by one prestigious journal, then accepted by the Transactions of the American Mathematical Society.
Nonetheless time passed, and after a while things began to appear in a different light. Stasheff's work was taken up into the theory of operads, of importance today in physics as well as in homotopy theory. Independently, around 1978 these structures were rediscovered, but this time by combinatorialists instead of topologists. The combinatorial structure of associahedra was specified as I have given it here in a paper by Huguet and Tamari, and it was asserted without proof by them that this was the face-graph of a polytope. I am not sure what the background to that construction was, but Gil Kalai tells me that Tamari had been interested in general questions of associativity in algebra since his thesis of 1951.
It was Kalai himself who named this structure an associahedron, and he called the problem of constructing the polytope explicitly to the attention of Mark Haiman, who then wrote down what was apparently the first detailed proof. From that point on, the subject expanded rapidly, but Stasheff's priority and the connection of associahedra with homotopy theory was not recognized by the combinatorialists until Mikhail Kapranov pointed it out. He was one of the first to extend significantly the family of associahedra to include other polytopes of combinatorial interest. The interest in associahedra and related polytopes continues to rise. New relations with widely spread fields of mathematics are still appearing.
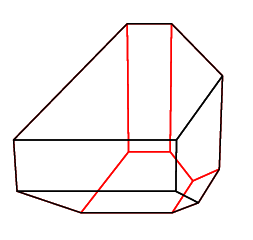
Developments have taken place in several different directions, all rather intriguing developments for such an intrinsically simple object. One closest to the original combinatorial invention is that explained in work of Satyan Devadoss (and a colleague or two) which associates a polytope rather explicitly to any finite graph whatsoever. Simplices come from a collection of unconnected nodes, associahedra from lines of connected ones. This is Devadoss' rendering of K5:

To find out more
- Satyan Devadoss, A realization of graph-associahedra, preprint, 2007.
- Mark Haiman, Constructing the associahedron This is a scan of his original manuscript with his proof, apparently the first found, that the associahedron is a polytope.
- Danièle Huguet and Dov Tamari, "La structure polyédrale des complexes de parenthésages", Journal of Combinatorics, Information & System Sciences 3 (1978).
- M. Kapranov, "The permuto-associahedron, MacLane coherence theorem and asymptotic zones for the KZ equation", Journal of Pure and Applied Algebra 95 (1993).
- Carl Lee, "The associahedron and triangulations of the n-gon", European Journal of Combinatorics 10 (1989). This was the first published proof.
- Jean-Louis Loday, Realization of the Stasheff polytope, Archiv der Mathematik 83 (2004), 267-278.
- James Stasheff, "Homotopy associativity of H-spaces I.", Transactions of the American Mathematical Society 108, 1963.
- James Stasheff, "From operads to physically inspired theories" available at various places on the Internet. The appendix by Stasheff and Snider was perhaps the first construction of the associahedron by truncating a simplex, eventually a standard technique.
- Günter Ziegler, Lectures on polytopes, Springer-Verlag, 1992. Filled with relevant stuff. In chapter 9, he discusses efficiently the theory of fiber polytopes, which extends the family of associahedra and has proven to be extremely useful in many branches of mathematics. This in turn originated in the secondary polytopes of Israel Gelfand, Mikhail Kapranov, and Andrei Zelevinski, an earlier surprising extension. Fiber polytopes have arisen most recently in the work of Gill Kalai's colleague Erez Lapid and his associates in some work on James Arthur's trace formula
Bill Casselman
University of British Columbia, Vancouver, Canada
cass at math.ubc.ca
Those who can access JSTOR can find some of the papers mentioned above there. For those with access, the American Mathematical Society's MathSciNet can be used to get additional bibliographic information and reviews of some these materials. Some of the items above can be accessed via the ACM Portal , which also provides bibliographic services.


















