Bin Packing
Posted May 2004.
1. Introduction
If you live in a city apartment, finding room to store your possessions is a major problem--there never seems to be enough room. Suburban residents must be having similar problems because the growth in using off-site storage facilities is on the rise. Metaphorically, there never seem to be enough bins for all one needs to store. Mathematics comes to the rescue with the bin packing problem and its relatives. The bin packing problem raises the following question: given a finite collection of n weights w1, w2, w3, ... , wn, and a collection of identical bins with capacity C (which exceeds the largest of the weights), what is the minimum number k of bins into which the weights can be placed without exceeding the bin capacity C? Stripped of the mathematical formulation, we want to know how few bins are needed to store a collection of items. This problem, known as the 1-dimensional bin packing problem, is one of many mathematical packing problems which are of both theoretical and applied interest in mathematics.
It is important to keep in mind that "weights" are to be thought of as indivisible objects rather than something like oil or water. For oil one can imagine part of a weight being put into one container and any left over being put into another container. However, in the problem being considered here we are not allowed to have part of a weight in one container and part in another.
One way to visualize the situation is as a collection of rectangles which have height equal to the capacity C and a fixed width, whose exact size does not matter. When an item is put into the bin it either falls to the bottom or is stopped at a height determined by the weights that are already in the bins.
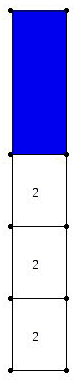
The diagram below shows a bin of capacity 10 where three identical weights of size 2 have been placed in the bin, leaving 4 units of empty space, which are shown in blue.
By contrast with the situation above, the bin below has been packed with weights of size 2, 2, 2 and 4 in a way that no room is left over.
Joseph Malkevitch
York College (CUNY)
Email: malkevitch@york.cuny.edu
- Introduction
- Basic ideas
- More approaches to bin packing
- Applications of bin packing
- References
Welcome to the
Feature Column!
These web essays are designed for those who have already discovered the joys of mathematics as well as for those who may be uncomfortable with mathematics.
Read more . . .
Feature Column at a glance