Mathematics and Cosmology
Posted April 2005.
There are a surprisingly large number of ways that mathematics has supported our attempts to understand the universe..
Joe Malkevitch
York College (CUNY)
malkevitch at york.cuny.edu 
Introduction
If you live near a major urban area as I do, the night sky features the moon, a few bright stars and an occasional glimpse of a planet. But many years ago when I was in South Dakota, on a very clear night I could see virtually to the horizon in all directions. This was my most personal encounter with the cosmos. There are certainly a lot of stars out there, more than books or living near New York City had given me a clue to. Perhaps one of the specks of light I saw was this object, now made more visible by mankind's ingenuity.
|
|
|
(Image of galaxy NGC 4414, courtesy of NASA.)
|
Although it may appear that understanding the universe in which we live is far removed from mathematics, this is not true. There are a surprisingly large number of ways that mathematics has supported our attempts to understand the universe. First, there is the question of the nature of the matter which makes up the cosmos. Mathematics has played a big role in understanding the subatomic particles which form the matter of living things, planets and stars. Second, geometers have been working with physicists and astronomers to understand the geometry of the space we live in. Whereas mathematicians might view alternative geometries as "different games" which are fun to investigate because their properties are so varied, physicists are concerned with what is space and its nature.
The mathematics involved in both of these areas gets very technical. This being Mathematics Awareness Month, with this year's theme Mathematics and the Cosmos, I will try to put in perspective how mathematics has played an essential role in the way humankind has come to view the cosmos.
The origins of the study of cosmology
The history of cosmology has two important threads: the history of the geometry of space as it evolved both in the mathematics and physics communities, and the history of astronomy, broadly interpreted.
Let us begin with a history of astronomy. It is a sign of human concern with cosmological issues that all ancient cultures took an interest in astronomy, sometimes independently and sometimes building on earlier interest. Work related to astronomy was carried out in Egypt, Babylonia, China, India, Mexico (the Maya), and Greece. Interest in the stars in ancient times combined an interest in astrology and astronomy. Astrology was concerned with the issue of the relationship between configurations in the heavens and human events. It must have been indeed scary for people during pre-scientific times to have seen such strange events as meteor showers, comets, and eclipses. Imagine having the sun suddenly disappear and having darkness descend.
Curiosity about the stars was one of the earlier manifestations of early science. A towering figure in this study was Claudius Ptolemy. Ptolemy's work had an enormous effect on the history of astronomy and cosmology. He developed a system that tried to explain the apparent motions of the planets under the assumption that the earth was the center of the universe. This required that the sun and planets' motions had to be explained in terms of the earth's being still, as it seemed to be, and that the sun and planets moved around the earth.
After the decline of Greek culture, the development of interest in astronomy was kept alive in the Islamic world, where mathematics was used in support of observational studies. Some of this concern with astronomy stemmed from an interest in charting the time for prayers, tracking important religious holidays using the lunar calendar, and knowing the direction to Mecca.
Although even in ancient times there had been individuals who were suspicious of a cosmology which placed the earth at the center of the universe, their opinion was largely ignored. Much later Copernicus (1473-1543) put forward the theory that the earth moved around the sun. There was great turmoil between holding on to older well-established ideas and trying to prove that the new approach was correct.
Theory and experiment
How has progress in our insights into the cosmos been made? Science proceeds by a delicate interplay of theory and experiment. Sometimes an experimentalist produces careful data over a long period of time which suggests the route for codifying a new theory based on the data. Other times, theory suggests experiments which make it possible to have much greater confidence in that theory. An example of the first type of progress is given in the interaction of the great Danish astronomer Tyco Brahe. It is somewhat ironic that Brahe publicly remained an adherent to his own variant of an earth-centered universe. His concern with the Copernican approach was being able to achieve sufficient verification. His empirical studies laid the foundation for a great leap forward in being able to give confirmation for a heliocentric view.

Brahe's careful observations with better designed and more carefully constructed instruments than his immediate predecessors resulted in very detailed information in the realm of observational astronomy. Even though he used only the naked eye, his observations were unusually reliable, as was to be verified by Johannes Kepler (1571-1630). Using Brahe's data, Kepler was able to formulate "guesses" as to what "laws" were governing the behavior that was being observed experimentally. Kepler used some of the data to generate proposed orbits and then used other data values as "proof" that the formulas he was generating were correct.
With Kepler's work the value of analytical thinking in support of cosmology made a great leap forward.

Based on Brahe's work and his own insights Kepler arrived at the formulation of "laws," now known as Kepler's Laws, that govern the "local cosmos:"
* The planets move around the sun in a path which is an ellipse with the sun at one of the foci.
* As the planet moves around the sun, a line joining the planet to the sun sweeps out equal areas in equal periods of time.
* For any two planets the squares of the periods of their revolution around the sun has the same ratio as the cubes of their average (mean) distances from the sun.
Johannes Kepler offers an interesting example of the complex ways that a person's milieu and way of thinking govern his/her abilities to understand the world. Kepler did his work at a time when scholars did not have as developed an infrastructure to work in as they do today. For example, journals to publish creative work had yet to be established. Despite this there was a surprising amount of interaction for active scholars by correspondence and personal contact. Kepler's work in some areas was way ahead of its time, but also preserved the past. Thus, Kepler reported on the work of Pappus of Alexandria about Archimides' work on what today are known as the 13 Archimedean polyhedra. From a modern perspective the regular convex polyhedra (also known as the Platonic solids) can be thought of as solids where all the faces are congruent regular polygons with the same number of sides, and where the faces all have the same pattern at each vertex. Two tetrahedra pasted together along a face would not be regular because although all the faces are congruent equilateral triangles, some vertices would have three triangles at a vertex while others would have four triangles at a vertex. Archimedes allowed different kinds of convex faces but wanted the vertex patterns at every vertex to be the same. Kepler also did pioneering work on tilings and sphere packings. Although there are a variety of very innovative and "oddball" mathematical musings in Kepler's work, his talents as a mathematician are not in the same league as those of Archimedes (who came before him) or Newton (who came after). Yet Kepler was a practicing astrologer (probably out of economic necessity), while Newton was a practicing alchemist!
Kepler used the regular polyhedra as a basis for a cosmological system which today looks like a very strange approach for such a very creative and smart man. However, it grew out of his great interest and insight into polyhedra At the time Kepler attempted to construct a cosmology based on the Platonic solids, believers in an earth-centered (geocentric) theory thought there were seven planets. This was because the earth's moon was treated as a planet in this system! Under the Copernican approach there were six planets known at the time (Mercury, Venus, Earth, Mars, Jupiter, and Saturn). The earth's moon now had to be treated in a separate category. There are five "spaces" between six planets, and it was in dealing with the varied sizes of these spaces that Kepler devised a cosmology based on the five regular solids.
Towards a modern cosmology
Galileo (1564-1642) played a critical role in the development of a modern cosmology. Although many people think of Galileo as a physicist, in fact, he first earned income by teaching mathematics. Eventually (1589) he took a position at the University of Pisa, where he had studied earlier under the mathematician Filippo Fatoni. In 1592 he moved to Padua to teach mathematics. (His chief duty was to teach the works of Euclid.) The history of cosmology changed dramatically in 1609 when Galileo was informed in a letter from a friend about the invention of a device using a lens which made it possible to view distant objects more clearly. Galileo immediately began making telescopes, and towards the end of 1609 made some dramatic discoveries. He described these discoveries in his book The Starry Messenger, published in 1610. He stated that he had seen mountains on the Moon, stars in the Milky Way, and four objects moving about the planet Jupiter. Galileo's observations immediately showed that the idea that all heavenly bodies orbited the earth was incorrect. Galileo continued his work in observational astronomy, being among the first to make observations of Saturn, though the resolution of his telescopes did not enable him to realize that Saturn was girdled with rings.
Galileo and Kepler lives overlapped, though Galileo lived much longer. They corresponded over a long period. Kepler encouraged Galileo to publish and popularize his thoughts on the heliocentric theory. Galileo mentions Kepler very rarely in his work and seems to have used some of his ideas without attribution. In his famous book Dialogues on the Two Great World Systems, Galileo mocks Kepler for speculating that the earth's tides are caused by the moon. Galileo's own theory about the tides turned out to be mistaken.

Galileo would certainly have been surprised and would have enjoyed the images below made possible by work he helped set in motion.


(Top: Saturn's rings including some of Saturn's moons; Below: A close-up of Saturn's ring structure. Courtesy of NASA)
What is amazing about Isaac Newton (1642-1727) is that he is rightly on both any short list of greatest mathematicians and of greatest physicists. Newton's great intellectual curiosity drove him to fathom the cosmology of the universe as it could be understood in the 17th century and to develop new mathematical tools to assist him in understanding the questions in physics that interested him. It is not an accident that Newton made contributions both as an experimentalist and a theoretician. His work on the reflecting telescope (1672) grew out of his insight into the need for data to be consistent with theory.

At this point it is perhaps worthwhile to comment briefly on the interplay between mathematics and the "real world." In the 20th century we have seen the development of the subfield in mathematics known as mathematical modeling. This part of mathematics concerns itself with the systematic study of the way that mathematics interacts with and can be applied in the "real world." Although formal attempts to study the modeling process are quite recent, the "abstraction" of how mathematics plays a part in the world is quite old, and there is no better "playground" in which to look at this interaction than the study of cosmology.
The details of our solar system, the first realm of concern in attempts to study cosmology, are very varied and complex. Early physical scientists (e.g. Ptolemy) understood the need to explain eclipses of the moon and the sun, the phases of the moon, and various motions of the stars. To do this they simplified. This is the essence of mathematical modeling: controlled simplification. One makes simplifying assumptions, uses deductive reasoning about this simplified world (the mathematical model) and then sees if the resulting conclusions accord enough with the "real world" to accept the model or to try to improve it. If the model roughly explains the data, if one has the mathematical tools to do so, one wants to tinker with the model to get it to explain the data better.
When Copernicus suggested that the over 1000-year tradition in explaining the nature of cosmology (the sun moves around the earth) was incorrect, he used a simplified model of circular motion for the earth around the sun. Even though the truth is that the earth's orbit is closer to an elliptical than a circular orbit, this orbit, as ellipses go, is very close to a circle. Yet Ptolemy's model had been so carefully honed over the centuries that it better predicted the motions of the heavenly bodies than Copernicus' new, and more correct, model. Kepler worked very hard on the computational side to demonstrate the accuracy of the heliocentric view of the solar system. He took Brahe's very accurate data and coupled it with an empirically based approach to finding the right curve to fit the data that Brahe had made. Eventually, he realized that an ellipse gave the closest fit for the Mars data, and then, having hit on the idea of elliptical orbits for the planets, verified that the planets other than Mars also move along ellipses. I am sure that Kepler would have been wowed by the following images from Mars. NASA's spacecraft arriving successfully at Mars represents a culmination of work on orbit calculations that Kepler set in motion.


(Images courtesy of NASA)
Once Kepler completed the formulation of his three laws of motion for the planets, it became possible for Newton's new model (universal gravitation with an inverse square law) to become the new "standard model," replacing Ptolemy and confirming Copernicus' and Kepler's views.
In Newton's lifetime the (Royal) Greenwich Observatory was created and directed by the Astronomer Royal. The people who have held that title are listed below:
John Flamsteed 1675 – 1719
Edmond Halley 1720 – 1742
James Bradley 1742 – 1762
Nathaniel Bliss 1762 – 1764
Nevil Maskelyne 1765 – 1811
John Pond 1811 – 1835
George Airy 1835 – 1881
William Christie 1881 – 1910
Frank Dyson 1910 – 1933
Harold Spencer Jones 1933 – 1955
Richard van der Riet Woolley 1956 – 1971
Martin Ryle 1972 – 1982
Francis Smith 1982 – 1990
Arnold Wolfendale 1991 – 1995
Martin Rees 1995 –
(In recent times the title is not associated with directing the Greenwich Observatory. Greenwich's proximity to large metropolitan areas has resulted in its no longer being used as an observational center.) The list above contains a variety of people whose names will be recognized by mathematicians. It is important to notice that when mathematics cooperates and takes an "interest" in another subject, invariably both subjects benefit. Here is a very small example of this phenomenon. Although George Airy had a very distinguished career as an astronomer he is now below the radar of most mathematicians.

Yet he retains a small footnote in contributing to mathematics via the attachment of his name to Airy Functions.
The great mathematicians of the post-Newton period were often equally important for their contributions to physics and astronomy. Among these many individuals were Karl Gauss (1777-1855), Pierre Simon de Laplace (1749-1827), and Leonhard Euler (1707-1783). I am sure that Gauss would have been pleased to see the image of Saturn's moon Phoebe (below) because in his position as director of the Göttigen observatory (from 1807 until his death), he was interested in computing the orbits of small astronomical bodies, having assisted in calculating the orbit of the asteroid Ceres.

(NASA image)
Modern cosmology
It is difficult so say when a modern view of cosmology emerged but one of the landmark figures who made the transition possible was James Clerk Maxwell (1831-1879), without whose famous equations connecting electrical and magnetic phenomena, dramatic progress could not have been made.
Much of modern cosmology begins with Edwin Hubble's (1889-1953) discovery of the seeming expansion of the universe with a linear law of expansion.

One way to visualize what might be happening in our universe would be to imagine what happens to points as the radius of a sphere uniformly increases. Under these circumstances a finite collection of points on the surface of the sphere (think of these as "galaxies") would have mutual distances which grow. Hubble's Law and the discovery of Cosmic Microwave Background Radiation (by A. Penzias and R. Wilson in 1965, for which they won a Nobel Prize) developed into what has come to be known as the Big Bang theory for the origin of the universe. The development of this theory played out against the maturing of such developments in physics as quantum mechanics, special relativity theory, and general relativity theory. There were also spectacular developments in understanding the structure of subatomic particles. However, despite all of the progress, there was no theory that put together what was happening on a very small scale (quantum mechanics and the forces governing subatomic particles) with what was occurring on a large scale (gravity and general relativity). The development of string theories seemed to offer a way to make this connection. String theory owes its origins to some work of mathematician Leonhard Euler (on the Beta function) which inspired physicists Gabriele Veneziano and Mahiko Suzuki, and offers a connection between general relativity theory and gravity. However, there are many "string theories" and at least so far, no single path offered by string theory has emerged as the way to proceed. Furthermore, no string theory offers experimental choices which could be carried out today and, thus, would resolve which of the many lines of theory might be what is true in the actual universe.
As mature as the progress in understanding our cosmos has gotten to be, it is helpful to remember the "kickers" that the history of science has provided. At the turn of the 19th to 20th century, Newton's approach to cosmology was riding high and had many predictive triumphs (the discovery of Neptune) to suggest its accuracy. However, Albert Einstein's (1879-1955) contributions were soon to show that Newton's laws were not the whole picture and that certain large-scale modifications had to be made to them. Intriguingly, Einstein's use of curvature concepts is built on the work of Gauss and Riemann.

Another physicist who captured the world's imagination with his use of mathematical reasoning in support of cosmology is Stephen Hawking (1942- ).

Hawking did seminal work on understanding the structure of the phenomena known as black holes. His theoretical work has resulted not only in a wide variety of observational work to try to understand black holes, but also in the theoretical exploration of new kinds of black holes. Hawking's work has also had unexpected ramifications for information theory. What happens to "information" that enters a black hole has become an important topic of interest to theorists.
As persuasive as Big Bang theory is, there are those who remain unconvinced of its truth. For example, I. E. Segal published attempts to explain existing data using a different model. Furthermore, recent discoveries of what appears to be an unexpected acceleration in the way that various locations in the universe are receding from each other do not fit into the model of cosmology that was being used. In the long run, the development of experimental tools (e.g. Hubble telescope, Cassini space probe) for understanding our cosmos, far and near, are as important as the current state of our theoretical insights. Although string theory appears to be a way to get insight into physical reality, its value as a mathematical theory unto itself, and its role as a catalyst in discovering new and better honed mathematical tools, may turn out to be its most important legacy. Two mathematicians who have tried to synthesize the current state of our understanding are Roger Penrose (1931- ) and Edward Witten (1955- ).

(Roger Penrose)

(Edward Witten)
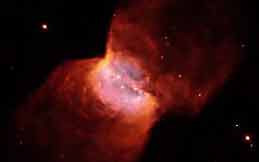
For those who want to explore the connections between mathematics and cosmology there are many entry points. There are no doubt many surprises down the path of mankind's efforts to better understand the universe in which we live. Mathematics will continue to be a major part of those efforts. Perhaps the following exotic stellar object will inspire you to do some work in this area.
Joe Malkevitch
York College (CUNY)
malkevitch at york.cuny.edu 
References
Abetti, G., The History of Astronomy, H. Schuman, New York, 1952.
Adler, K., The Harmonious Universe, Prometheus, Amherst, New York, 2004.
Ball, R., Great Astronomers, Isbister, London, 1895.
Bartusiak, M., (ed.), Archives of the Universe: A Treasury of Astronomy's Historic Works of Discovery, Pantheon, New York 2004.
Buchler, J. and S. Detweiler, J. Ipser, Nonlinear Problems in Relativity and Cosmology, Annals of the New York Academy of Sciences, Volume 631, 1991.
Caspar, M., Kepler, Abelard-Schuman, London, 1959.
Cohen, I., Newton's method and Newton's style, in Newton: Texts, Background, Commentaries, I. Cohen and R. Westfall, (eds.), Norton, New York 1995.
Cohen, I. and R. Westfall, The Newtonian Revolution: With Illustrations of the Transformation of Scientific Ideas, Cambridge U. Press, Cambridge, 1980.
Cornford, F. Plato's Cosmology, Cambridge, London, 1937. (A translation of the Timaeus.)
Daigneault, A. and A. Sangalli, Einstein's static universe: an idea whose time has come back?, Notices Amer. Math. Soc. 48 (2001) 9-16.
de la Torre, L., Math is key to identifying source of "strange foot-print", Physics Today 15 (1997) 102.
Dreyer, J., A History of Astronomy from Thales to Kepler, Dover, New York, 1953.
Field, J., Kepler's Geometrical Cosmology, University of Chicago Press, Chicago, 1988.
Gorst, M., Measuring Eternity, Broadway Books, New York, 2001.
Grabiner, J. Newton, Maclurin, and the authority of mathematics, Amer. Math., Monthly, 111 (2004) 841-852.
Grant, R., History of Physical Astronomy, Henry Bohn, London, 1852.
Greenberg, J., The Problem of the Earth's Shape from Newton to Clairaut, Cambridge U. Press, New York, 1995.
Greene, B., The Fabric of the Cosmos: Space, Time, and the Texture of Reality, Norton, New York, 2004.
Greene, B., The Elegant Universe: Superstrings, Hidden Dimensions and the Quest for the Ultimate Theory, Norton, New York, 1999.
Guth, A., Inflationary Universe: A Possible Solution to the Horizon and Flatness Problems, Physical Review D 23 (January 15, 1981) 347-56.
Guth, A., The Inflationary Universe, Addison-Wesley, Reading, 1997.
Hawking, S. and G. Ellis, The Large-Scale Structure of Space-Time, Cambridge U. Press, Cambridge, 1973.
Hawking, S., A Brief History of Time, Doubleday, New York, 1998.
Hawking, S., Black Holes and Baby Universes and Other Essays, Bantam, New York, 1993.
Hawking , S. and R. Penrose, The Nature of Space and Time, Princeton U. Press, Princeton, 1996.
Kaku, M., Parallel Worlds: A Journey Through Creation, Higher Dimensions, and the Future of the Cosmos, Doubleday, New York, 2005.
Kepler, J., Mysterium Cosmographicum, A. Duncan, translator, Abaris, New York, 1981.
Kepler, J., New Astronomy, W. Donahue, translator, Cambridge U. Press, Cambridge, 1992.
Kepler, Epitome of Copernican Astronomy, C. Wallis, translator, Prometheus Books, Amherst, New York, 1995.
Leff, H. and A. Rex, Maxwell's Demon, Princeton U. Press, Princeton, 1990.
López-Corredoria, M., Observational Cosmology: caveats and open questions in the standard model (preprint: July 7, 2004)
Lerner, E., The Big Bang Never Happened, Random House, New York, 1991.
Niven, L., N-Space, Tom Doherty Associates Books, New York, 1990.
Pecker, J., Some critiques of the Big Bang Cosmology, presented at a conference, The Big Bang and Alternate Cosmologies, Bangalore, India, 1997.
Peebles, P., Principles of Physical Cosmology, Princeton U. Press, Princeton, 1993.
Penrose, R., The Road to Reality: A Complete Guide to the Laws of the Universe, Random House, New York, 2005.
Rainer, M. and H. Schmidt, Current Topics in Mathematical Cosmology, World Scientific, Singapore, 1998.
Reichen, C., A History of Astronomy, Hawthorn Books, New York, 1963.
Segal, I., Mathematical Cosmology and Extragalactic Astronomy, Academic Press, New York, 1976.
Segal, I. and J. Nicoll, Astronomy phenomenological analysis of redshift-distance power laws, Astrophysics and Space Science, 274 (2000) 503-512.
Smith, G., The newtonian style in Book II of the Principia, In Isaac Newton's Natural Philosophy, J. Buchwald and I. Cohen, (eds.), MIT Press, Cambridge, 2000, p. 249-313.
Taylor, E. and J. Wheeler, Spacetime Physics, W.H. Freeman, San Francisco, 1963.
Tyson, N., Origins, Norton, New York, 2004
Tweddle, I., James Stirling, Scottish Academic Press, Edinburgh, 1988.
Thurston, H., Early Astronomy, Springer-Verlag, New York, 1996.
Weeks, J., The twin paradox in a closed universe, Amer. Math. Monthly, 108 (2001) 585-590.
Zebrowski, E., A History of the Circle, Rutgers U. Press, New Brunswick, 1999.
NOTE: Those who can access JSTOR can find some of the papers mentioned above there. For those with access, the American Mathematical Society's MathSciNet can be used to get additional bibliographic information and reviews of some these materials. Some of the items above can be accessed via the ACM Portal, which also provides bibliographic services.