Cubes
7. Symmetries of the cube
The symmetries of a figure X are the geometric transformations (one-to-one, onto mappings) of the figure X onto itself which preserve distance, in our case, Euclidean distance. Symmetries which preserve distance are known as isometries. If f and g are two symmetries of X, the "product" formed by first performingf and then performing g is also a symmetry of X. It is important to note that g followed by f will not in all cases be the same symmetry as f followed by g. The mathematical structure consisting of the symmetries of a figure X together with the operation of performing one symmetry after another is called the symmetry group of X. The number of elements in a symmetry group is called the order of the symmetry group. Loosely speaking, figures with more symmetry have symmetry groups of larger order.
The symmetry (isometry) group of the 3-cube has 48 elements. To give you a sense of comparison, the regular tetrahedron has a symmetry group of 24 elements and the symmetry group of the regular dodecahedron and regular icosahedron have order 120. The isometries for the cube are rotations and reflections. Note that the symmetry group of the 3-cube is not the same as the group of rotations of the cube about some line. The rotation group of the 3-cube only has 24 elements.
If you are having trouble seeing what is going on here, consider the simpler case of the symmetry group of the 2-cube, the square, and the rotation group of the square.
The rotation group of the square has 4 elements. To write down the symmetries of the square we will use the well-known cycle notation for permutations of the number which represent the vertices of the square.
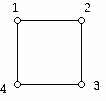
Thus, (13)(24) represents the mapping which takes vertex 1 to vertex 3 and vertex 3 to vertex 1, and vertex 2 to vertex 4 and vertex 4 to vertex 2. The notation (1), for example, signifies that vertex 1 is unmoved.
We have the following rotational symmetries:
0 degree rotation: (1)(2)(3)(4)
90 degree rotation clockwise: (1234)
180 degree rotation clockwise: (13)(24)
270 degree rotation clockwise: (1432)
However, the symmetry group of the square includes other symmetries that do not arise from translations or rotations. These symmetries arise by reflections and thus carry the square into a higher dimensional space in order to physically carry them out!
As an abstract group, the rotations of the square form the cyclic group on 4 elements. However, the symmetry group for the square is the dihedral group D4 of order 8 and the additional permutations in this group are:
(1)(3)(24)
(2)(4)(13)
(12)(34)
(14) (23)
In an analogous way, the rotation group of the 3-cube has 24 rotations. Abstractly, this group is isomorphic to the 24 different permutations of 4 symbols. The full symmetry group of the cube, however, has 48 elements. These additional symmetries arise from the reflections of the cube that are isometries but which can not be carried out physically in 3-dimensional space.
For the n-cube it will probably not surprise you that there are a lot of symmetries. In fact, the size of the symmetry group of the n-cube is 2n(n!), which grows very rapidly.
-
Introduction
-
Some history
-
The 3-dimensional cube
-
Combinatorial perspectives on cubes
-
A recursive way of constructing cubes
-
Cube puzzles
-
Symmetries of the cube
-
The Sharir-Ziegler cube
-
References
Welcome to the
Feature Column!
These web essays are designed for those who have already discovered the joys of mathematics as well as for those who may be uncomfortable with mathematics.
Read more . . .
Feature Column at a glance



