Descartes 2 Descartes's Lost Theorem
The strange history of Descartes's Treatise
Descartes never published his Treatise on Polyhedra; the manuscript was inventoried among his papers after his death in Stockholm in 1650. These papers passed into the possession of his friend Hector-Pierre Chanut, the French ambassador to Sweden, and from him to his brother-in-law, Claude Clerselier, who had become Descartes's principal correspondent in France.

Gottfried Wilhelm,
Freiherr von Leibniz
1646-1716 | In 1675 and 1676, when Leibniz was in Paris, he had access to Descartes's papers chez Clerselier. He made copies of many of them and in particular a copy of the Treatise in his own hand. The copy remained among Leibniz's papers after his death, unrecognized and still unpublished. Some hints by biographers and in Leibniz's correspondence led to its discovery towards the middle of the nineteenth century (by then, the original manuscript had disappeared). |
The complete reestablishment of the text required expertise in the deciphering of Leibniz's handwriting and the correct interpretation of certain ``cossic'' symbols for variables, squares, and cubes, with which Descartes
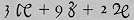
Cossic notation for 3 x3 + 9 x2 + 2 x. followed the usage of Clavius and the Italian algebraists of the beginning of the seventeenth century. This story, as well as the version I have followed, is that given in the Adam-Tannery Oeuvres de Descartes, Vol. X, Paris 1908.
Part of the interest that greeted the discovery of the Treatise was due to the equivalence between Descartes's Lost Theorem and a very famous theorem of Leonhard Euler. By Euler's time, scientific journals existed, and his theorem and its proof were published in two consecutive articles in the Communications of the St. Petersburg Academy for 1752-53.
On to next Descartes page.
Back to first Descartes page.
Welcome to the
Feature Column!
These web essays are designed for those who have already discovered the joys of mathematics as well as for those who may be uncomfortable with mathematics.
Read more . . .
Feature Column at a glance



