dna-abc2 The ABC of DNA Computing
2. The Directed Hamiltonian Path Problem
The Directed Hamiltonian Path Problem problem involves an oriented graph. This means a collection of points (vertices) and of arrows (oriented paths) from one point to another. A nice way to think about the problem (following Fred Hapgood) is to turn the graph into the route map for an airline:
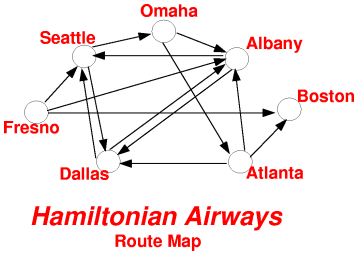
each vertex represents an airport and each arrow represents a flight from one airport to another. We designate a Start airport (say, Fresno) and a Finish (say, Boston). In these terms, the directed Hamiltonian path problem for this graph is to find a sequence of flights beginning in Fresno, ending in Boston and visiting each airport in the route map exactly once. In usual graph terminology, such a sequence is called a
Hamiltonian path.
- This problem is simple to state and, when there are only few airports and flights, can be solved by inspection.
- But the amount of computation necessary to settle the question, using the most efficient algorithms known at present, grows exponentially with the size of the route map: essentially the only way is to go down the list of all possible chains of flights until a solution is found or until the list is exhausted.
- On the other hand given any list of airports, even in a very large graph, checking if that list defines a Hamiltonian path or not just means checking for each airport if one of its flights leads to the next airport on the list. The number of computations is bounded by some constant times the number of airports times the maximum number of flights leaving an airport.
The combination of exponential growth of the list to be searched, and polynomial growth of the length of the checking algorithm, makes this an NP problem.



