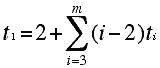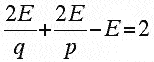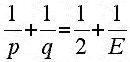Euler's Polyhedral Formula: Part II
Posted January 2005.
So much power from just the simple relationship: Vertices + Faces - Edges = 2 . . .
Joseph Malkevitch
York College (CUNY)
malkevitch at york.cuny.edu 
1. Introduction
Occasionally a mathematical fact is so significant that the results it leads to give insights which range widely over a large area of mathematics and its applications. This is true of Euler's seminal polyhedral formula. Not only did the result lead to deep work in topology, algebraic topology, and the theory of surfaces in the 19th and 20th centuries, but the result has also had great significance for combinatorics, graph theory, computational geometry, and other parts of mathematics. This research continues to be actively pursued today. So much power from just the simple relationship: Vertices + Faces - Edges = 2.
2. Euler relations
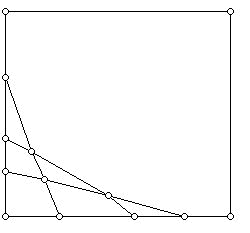
Using Euler's polyhedral formula for convex 3-dimensional polyhedra, V (Vertices) + F (Faces) - E (Edges) = 2, one can derive some additional theorems that are useful in obtaining insights into other kinds of polyhedra and into plane graphs. A plane graph is a diagram consisting of dots (vertices) and line segments (edges) which can be drawn in the plane so that the line segments meet only at vertices. (More on graphs can be found here.) A graph is called regular if all its vertices have the same degree or valence - the number of edges that meet at that vertex.
For what values of k is it possible for a convex polyhedron to have a k-regular graph? It turns out that it is easy to verify from Euler's formula that k can only be 3, 4, or 5. (For arbitrary plane graphs one can also have the case that k = 1 or k = 2.)
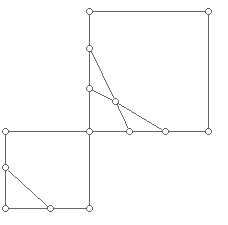
Let us denote by pk (as has become standard) the number of faces of a plane graph with k sides. We can illustrate this notation using the plane graph shown in the diagram below, which also illustrates a 3-valent graph. Each of its vertices has exactly three line segments at a vertex. Note that the line segments are straight line segments and that all of the faces are convex regions except for the 6-gon region which represents the "infinite face."

Figure 1
In this plane graph above, we have: p3 = 2, p4 = 3, p5 = 1, p6 = 2, and p7 = 1.
Since each edge of the graph is counted in two faces, we have that the following equation must hold in general:
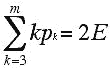
(*)
where m denotes the number of sides of the largest face in the graph. (Graphs which arise from convex polyhedra can not have faces with 1 or 2 sides, but one can easily extend the discussion to handle that case as well.)
We can obtain a relationship that must be satisfied by the values of a k-valent graph. Since every edge also has exactly two endpoints, in a 3-valent graph we have that:
Substituting in Euler's polyhedral formula multiplied by 6 we get:
which gives:
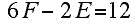
(**)
Using equation (*) above and the fact that
and again substituting in (**) and simplifying, we obtain:
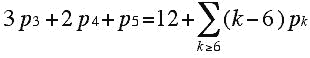
(***)
What is remarkable about this equation is that there is no restriction placed on the number of six-sided faces that are present in a plane 3-valent graph. One can derive analogous formulas for 4-valent and 5-valent plane graphs. A general question is: Which sets of non-negative integers that satisfy the "Euler relation" above can arise as the numbers of faces of a 3-valent convex polyhedron? Another question is whether or not a diagram such as the one in Figure 1 can arise from a convex polyhedron.
3. Steinitz's Theorem
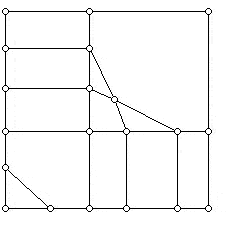
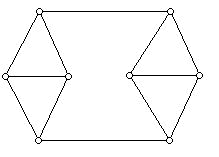
An argument of Cauchy's (1789-1857) shows that if G is the edge-vertex graph of a convex 3-dimensional polyhedron, then G is a planar graph. Furthermore, since a polyhedron can not have fewer than three edges at any vertex or any faces with fewer than 3 sides, these are obvious necessary conditions that a graph must obey in order for it to be the edge-vertex graph of some convex 3-dimensional polyhedron. However, these conditions are not sufficient for a graph to arise from a convex polyhedron. Clearly, a graph corresponding to a polyhedron can not have a single edge whose removal disconnects the graph into more than one piece, as would be true for the graph below:
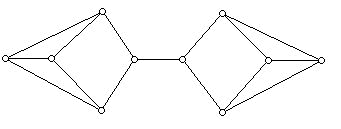
The graph below is 3-valent and has faces which are at least three-sided. Can you convince yourself that it does not correspond to any convex 3-dimensional polyhedron, but that there is a non-convex 3-dimensional polyhedron which does have this as its edge-vertex graph? The polyhedron, when you find it, has four triangular faces and two hexagonal faces!
In a rather curious situation, the solution to this problem, finding conditions on a graph that it be isomorphic to (have the same structure as) the vertex-edge graph of a convex 3-dimensional polyhedron, was completely answered in the early part of the 20th century. This work was done by the great German geometer and algebraist Ernst Steinitz (1871-1928).
Steinitz's work was published in German and, unfortunately, did not become widely known for quite some time. The catalyst for the reformulation of what Steinitz had done was the "translation" of his work into modern graph theory terminology. This was done by the distinguished geometer Branko Grünbaum.

Grünbaum became interested in polyhedra during his graduate studies in Israel and was focused by work he did with Theodore Motzkin (1908-1970) on the combinatorial structure of polyhedra.
Steinitz's Theorem (as reformulated by Branko Grünbaum):
A graph G is isomorphic to the vertex-edge graph of a 3-dimensional polyhedron (i.e. G is 3-polytopal) if and only if G is planar and 3-connected.
The property of being 3-connected requires that for any pair of vertices u and v of the graph, there are at least three paths between u and v whose only vertices in common are u and v. The diagram below offers a "schematic" view of what such paths might look like for two typical vertices in a graph. (The diagram omits other edges that might be present at the dots shown.)
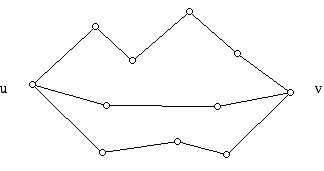
Amazingly, Steinitz's Theorem enables one to study the combinatorial theory of 3-dimensional convex polyhedra by drawing diagrams in 2 dimensions! Whereas there were almost no mentions of what Steinitz had done between the time when Steinitz published his original theorem and Grünbaum's reformulation, after the reformulation there was a flood of new results. These appeared in areas involving Hamiltonian circuits (a tour of the vertices, starting and ending at the same vertex, visiting each vertex once and only once), coloring problems, and matchings (disjoint sets of edges). Perhaps the greatest progress concerned existence theorems for 3-dimensional convex polyhedra. Such questions now were reduced to constructions of planar graphs.
The study of Hamiltonian circuits was spurred by the graph theory version of Steinitz's Theorem. Although William Tutte discovered n 1947 his famous example of a 3-valent 3-polytopal graph with 46 vertices which did not have a Hamiltonian circuit, work in this area took off after the appearance of Grünbaum's important book Convex Polytopes, which appeared in 1967. Thus, David Barnette (and others) found a 38-vertex, 3-valent, 3-polytopal non-Hamiltonian graph, and was led by his work to the still open conjecture that planar 3-valent 3-connected bipartite graphs have a Hamiltonian circuit. Another milestone in the theory of Hamiltonian circuits was Grinberg's amazing result, described below.
Let G be a plane graph with Hamiltonian circuit H, let pk' denote the number of k-gonal faces of G which are interior to the circuit H, and let pk'' denote the number of k-gonal faces of G which are exterior to the circuit H.
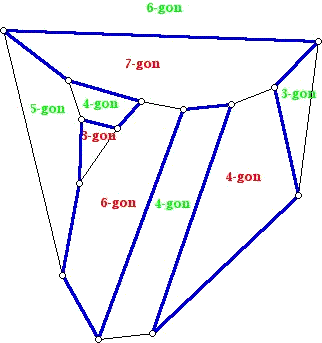
Figure 2
For the diagram above and the Hamiltonian circuit shown in blue we have four interior faces (labeled in red) which are a 3-, 4-, 6-, and 7-gon. The faces which are exterior to the blue Hamiltonian circuit (labeled in green) are a 3-gon, two 4-gons, a 5-gon, and a 6-gon. Grinberg's Theorem states that the following relationship must hold between the faces lying in the interior and exterior of such a Hamiltonian circuit:
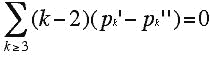
You should verify that the numbers associated with the Hamiltonian circuit in Figure 2 satisfy the equation above. As an example of the power of Grinberg's Theorem, one can use it to show that the 3-valent polyhedron whose graph is shown below has no Hamiltonian circuit. The lack of a Hamiltonian circuit follows from the fact that all of the faces in the graph except one have a number of sides which leaves a remainder of 2 when divided by 3. (Put differently, all the faces have a number of sides congruent to two mod 3, except for one face, the 9-gon.) Although Tutte's 46-vertex graph contains sets of 3 edges which will disconnect the graph into two pieces, each of which contains a circuit, for the graph below, one has to cut 5 edges to disconnect the graph into two pieces, each of which contains a circuit.
4. Eberhard Type Theorems
Look again at the equation that a 3-valent plane graph must satisfy:
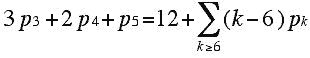
(***)
A natural question to ask is: Given a solution of this equation in non-negative integers, does there exist a convex 3-dimensional polyhedron P such that the number of sides of the faces of P are the given ones? For example, it is not difficult to see that p5 = 13 and p7 = 1 satisfy (***), but there is no plane 3-valent 3-connected graph with 13 pentagonal faces and 1 heptagonal face. However, because there is no restriction on the value of p6 for a plane graph, the following question arises. Given a solution S of (***) in non-negative integers, can one choose a value of p6 and construct a plane 3-connected graph that has the chosen value of p6 and the values of faces given by S? It was this problem that a blind 19th century geometer, Victor Eberhard, raised and thought he had solved in his book Zur Morphologie der Polyeder. Although Eberhard's "Theorem" was given by Eberhard, his proof does not meet modern standards of rigor. Branko Grünbaum, using Steinitz's Theorem, was able to give a proper proof of Eberhard's Theorem. However, the proof and some extensions and generalizations of the original proof and theorem are somewhat technical.
Branko Grünbaum considered the 4-valent analogue of Eberhard's Theorem whose proof is a tour de force and a mathematical gem. The Euler relation for plane 4-valent graphs is:
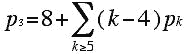
(****)
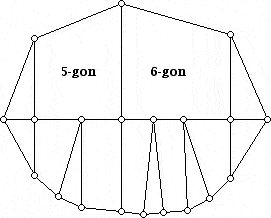
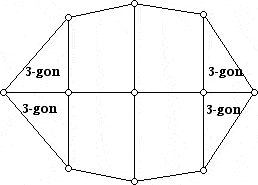
Here I will outline Grünbaum's original proof, which is very lovely and unexpected. Then I will show a slightly simpler proof (with easier-to-realize drawings). Rather than show a general proof, I will show an example which indicates how to proceed in the general case. First, note that what the 4-valent Euler relation tells us is that every 4-valent 3-polytopal graph (i.e. plane, 4-valent, 3-connected) has 8 triangles, and (k-4) additional triangles for each k-gon. Now, suppose we would like to find a 3-polytopal graph with p5 = 1 and p6 = 1, and we are allowed to use as many 4-gons as we would like, since they are unrestricted by the 4-valent Euler relation (****).
Grünbaum's proof constructs a square "block" for each of the k-gons (k ≥ 5). The block is constructed by placing k-4 dots along the left hand side and bottom of a square (note: these dots do not include those already at the corners). The dots are joined in the order of top dot on the left to the left dot on the bottom. Next, one joins the next dot down on the left to the next dot to the right on the bottom, etc.. Note that this results in a group of (k-4) triangles hugging a k-sided region in the square. The internal vertices in the block are 4-valent, and the other faces within the block are all 4-gons, which can be used as generously as we want.
One now takes the individual blocks, one for each k-gon, and lays them out along the anti-diagonal of an array. For blocks with a 5-gon and 6-gon we get the diagram shown below:
Grünbaum now adds additional horizontal and vertical edges to create the situation below. Note that in doing so only 4-gon regions are added, but we are allowed as many of these as we would like.
Notice also that all the interior vertices above are 4-valent and that the number of vertices along the left and bottom are equal. There are also equal numbers of vertices along the top and right hand side of the "array." The 4 corners of the square have valence two at this juncture and the other vertices have valence three.
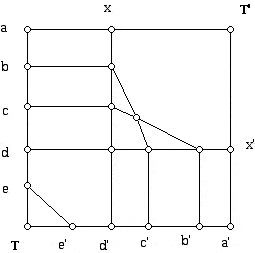
To finish his construction Grünbaum joins the vertices b and b', c and c', etc., and x and x' (in this example there is only one pair of such vertices but usually there will be many), etc. Finally, a is joined to a' with two curved lines, one going past T and the other past T', and T is joined to T' with two curved lines one going past a and the other past a'. You can verify for yourself by carrying this out and treating lines that cross as 4-valent vertices, that all of the new vertices are 4-valent, and that all the new faces with 8 exceptions are 4-gons. The 8 exceptional faces are triangles. Three of these are located near T and three are located near T'. Can you find the additional two triangles?
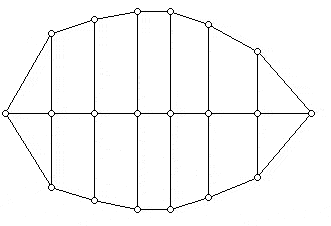
With Grünbaum's pioneering proof to inspire, other proofs were developed. The one that follows is due to Ernst Jucovic, a Czechoslovakian mathematician. We start with the graph depicted in the diagram below, where we would have used more "vertical" lines between the four indicated 3-gons had we wanted more k-gons (k > 4) in the final graph. The number of such verticals is one less than the number of k-gons to be added.
The diagram above is now modified by introducing (k-4) triangles for each k-gon to be added, as indicated in the diagram below for the 5-gon and 6-gon we wish to have. Note that there are fourteen 3-valent vertices in the graph shown. These vertices lie along the infinite face of the current drawing.
Also note that the vertices along the infinite face of the graph above are all 3-valent while all the internal vertices of the graph are 4-valent. To complete the construction we will use the graph shown below: This graph also has four 3-gons, and 4-gons with its internal vertices 4-valent, while the vertices on the infinite face are equal in number to the graph above (e.g. 14 vertices) and 3-valent.
If we place the graph with the k-gons (k > 4) on the northern hemisphere of a sphere, with the fourteen 3-valent vertices along the equator, and the diagram with only 4-gons and four triangles on the southern hemisphere of the same sphere matching up its fourteen vertices along the equator, the result is a graph with all 4-valent vertices, and exactly the right number of triangles and k-gons that we wish. Since all the other faces are 4-gons, and these are not restricted by the 4-valent version of Euler's equation, we have constructed a 4-valent plane 3-connected graph which has the properties that were asserted for the 4-valent Eberhard Theorem. One can also look at the values of p4 which can occur as the number of 4-gons for a plane 3-connected graph and which "realizes" the given solution of the 4-valent Euler relation.
Grünbaum's new look at Eberhard's original theorem and his 4-valent version opened a floodgate of interesting work related to this topic. For example, extending the 4-valent Eberhard Theorem, Dalyoung Jeong showed that for any face vector satisfying the 4-valent Euler relation (number of 4-gons not restricted) one can select a value for the number of 4-gons and construct a plane embedding of a valent 3-connected graph which realized the given face vector with the selected value of p4 and the resulting graph would be a projection of a knot! (Another way of thinking of this is that in the plane drawing, if one is moving along any edge and then takes the "middle choice" of edge when one gets to a vertex, the sequence of edges one generates in this manner forms an Eulerian circuit for the graph, a circuit that traverses each edge of the graph in one stroke.) Many attempts have been made to generalize Eberhard's theorem to other kinds of Euler relations. For example the valences of a tree (a connected graph without circuits) satisfy the equation below, where ti denotes the number of vertices of the tree which are i-valent:
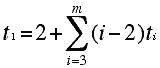
Since the coefficient of t2 vanishes in this equation, it is possible to formulate a variety of Eberhard type theorems for various classes of graphs which involve the spanning trees of these graphs.
5. Putting Euler's formula to use
One of the reasons why Euler's formula is on my list of most important theorems is its role in both the small and the large in supporting the development of new ideas and solving problems. A typical example is obtaining insight into the area of "regular polyhedra."
The Greeks seemed to have been the first to call attention to the question of what (convex) polyhedra have congruent regular polygons for faces, and that an equal number of faces meet at a vertex. In Euclid's Elements there is a metrical argument to prove that there are exactly 5 such regular polyhedra. However, one can prove a bit more using Euler's polyhedral formula. Namely, one can show that there are 5 combinatorially regular polyhedra, that is, there are only 5 types of polyhedra all of whose faces have the same number p (p ≥ 3) of sides and the same number of faces q (q ≥ 3) at each vertex.
To see this we note that if all the faces of a plane graph are p-gons, then we have that pF = 2E (where as usual F and E are the number of faces and edges of the graph, respectively) and we have qV = 2E, since every edge has exactly two endpoints. Substituting both of these into Euler's formula V + F - E = 2, we obtain:
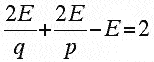
Simplifying, we obtain:
It is easily seen that since p and q must be at least 3, there are only 5 solutions of this equation in integers:
| p |
q |
E |
| 3 |
3 |
6 |
| 3 |
4 |
12 |
| 3 |
5 |
30 |
| 4 |
3 |
12 |
| 5 |
3 |
30 |
These rows correspond to the regular tetrahedron, the regular octahedron, the regular icosahedron, the cube, and the regular dodecahedron.
Modern insights into the semi-regular and Archimedean solids also involve the use of Euler's Formula. The idea here is to weaken the condition of regularity requiring that all faces be regular polygons to allow perhaps several different kinds of polygons, and the condition that the pattern of polygons around each vertex be identical. Pappus described 13 convex polyhedra that he attributed to Archimedes, though he did not mention the two infinite families, the prisms and anti-prisms. Later Kepler claimed to give a proof that there are 13 such solids, but in fact, there is a 14th solid that obeys these local regularity conditions. However, the modern definition of Archimedean has been altered to retain the count at 13. This definition requires that the symmetry group of the polyhedron be transitive on the vertices. (This means that there is an isometry, a distance-preserving transformation, of the polyhedron onto itself that moves any vertex to any other vertex.)
Euler's formula also played a role in a lovely generalization of the work set in motion by the Greeks, namely, the completion of a list of all of the convex 3-dimensional polyhedra which have only regular faces. For this work the requirement that all of the vertices of the solid be alike in any way is dropped. Only the regularity condition on the faces remains. Norman Johnson (a doctoral student of H.S.M. Coxeter) developed a conjecture that this collection of polyhedra is finite, once one excludes the two infinite families, the prisms and the anti-prisms. Johnson conjectured that in addition to the 5 regular convex 3-dimensional polyhedra and the 13 Archimedean 3-dimensional polyhedra, there are 92 convex solids with regular faces. He provided names for all of these solids, and he and Branko Grünbaum showed the important step that there could be only a finite number of such solids. In 1969, the Soviet Mathematician V. Zalgaller completed a proof that Johnson's list of solids was complete. These 92 solids are now known as the Johnson Solids. Even though they do not have as many special features as the regular polyhedra they are none the less very remarkable.
Euler's formula has a spawned a seemingly endless stream of mathematical results. May that stream never stop!
6. Acknowledgments
I blinked and three years have gone by. My term for writing the Feature Column has come to an end. I want to thank Tony Phillips, without whose encouragement I would not have started writing columns. Writing these has been a tremendous mathematical high, and I am glad to say that I will have a continuing role in the future of the column. In thinking over my experiences of the last three years I would like to thank all of the people who in ways direct and indirect have affected me and, hence, these columns. My continued interest in and love of mathematics in general, and geometry in particular has grown out of my interactions with Donald Crowe (U. of Wisconsin), Branko Grünbaum (University of Washington) and Walter Meyer (Adelphi University). I have also been continually inspired by the people who regularly and irregularly attend and make presentations at the Courant Institute Geometry Seminar (notably Jacob Eli Goodman, Janos Pach, and Richard (Ricky) Pollack). Many people have assisted with providing me with photographs and copies of their work. I thank them all. Professor Hope Young of the York College Library has been of great help in getting me a variety of obscure items. The staff of the library at the Courant Institute of Mathematical Sciences have also proved very helpful.
I have gotten tremendous encouragement and support for this column from the American Mathematical Society. In particular, Mike Breen and Annette Emerson of the Public Awareness Office, Sherry O'Brien and Timothy McMahon on the technical end, and John Ewing helped make it all possible. Finally, I would like to thank my family for sparing me the time to write these monthly columns, and my wife, Nina Greenberg Malkevitch, who found time to read every one of my columns and help out with improving their grammar, clarity, and effectiveness.
Joseph Malkevitch
York College (CUNY)
malkevitch at york.cuny.edu 
7. References
Aigner, M. and G. Ziegler, Proofs from the Book, 3rd. edition, Springer-Verlag,
Appel, K. and W. Haken, Every planar map is four-colorable, Bull. Amer. Math. Soc., 82 (1976) 711-712.
Barnette, D., Trees in polyhedral graphs, Can. J. Math., 18 (1966) 731-736.
Barnette, D., Wv paths on 3-polytopes, J. Combinatorial Theory, 7 (1969) 62-70.
Barnette, D., On p-vectors of 3-polytopes, J. Combin. Theory, 7 (1969) 99-103.
Barnette, D., Projections of 3-polytopes, Israel J. Math., 8 (1970) 304-308.
Barnette, D., Polyhedra, and the Four Color Theorem, Volume 8, Dolciani Mathematical Expositions, MAA, Washington, 1983.
Barnette, D. and B. Grünbaum, On Steinitz's theorem concerning convex 3-polytopes and on some properties of 3-connected graphs, in Many Facets of Graph Theory, Lecture Notes in Mathematics, Volume 110, Springer-Verlag, 1969, p. 27-40.
Barnette, D and B. Grünbaum, Preassigning the shape of a face, Pac. J. Math., 32 (1970) 299-302.
Beck, A. and D. Crowe, M. Bleicher, Excursions into Mathematics, Millennium edition, A.K. Peters, Wellesley, 2000.
Beineke, L. and R. Wilson, (eds.), Graph Connections, Clarendon Press, Oxford, 1997.
Biggs, N. and E. Lloyd, R. Wilson, Graph Theory 1736-1936, Clarendon Press, Oxford, 1986.
Bruggesser, H., and P. Mani, Shellable decompositions of cells and spheres, Math. Scand., 29 (1971) 197-205.
Cauchy, A., Recherches sur les Polyèdres - Premier Mémoire, Journal de l'École Polytechnique, 9 (Cahier 16) (1813) 68-86.
Dress, A., A combinatorial theory of Grünbaum's new regular polyhedra, Part II, Complete enumeration, Aequationes Math., 29 (1985) 222-243.
Eberhard, V., Zur Morphologie der Polyeder, Leipzig, 1891.
Euler, L., Elementa doctrinae solidorum, Novi Comm. Acad. Sci. Imp. Petropol., 4 (1752-3) 109-140 (published 1758), Opera Omnia (1) Volume 26, 72-93.
Euler, L., Demonstratio nonnullarum insignium proprietatum quibas solida hedris planis inclusa sunt praedita, Novi Comm. Acad. Sci. Imp. Petropol., 4 (1752-1753), 140-160 (published 1758) Opera Omnia (1) Volume 26, 94-108.
Fary, I., On straight-line representation of planar graphs, Acta. Sci..Math., (Szeged), 11 (1948) 229-233.
Fauvel, J. and R. Flood, R. Wilson, (eds.), Möbius and His Band, Oxford U. Press, Oxford, 1993.
Federico, P., Descartes on Polyhedra, Springer-Verlag, New York, 1982.
Felsner, S., Convex drawings of planar graphs and the order dimension of 3-polytopes, Order 18 (2001) 19-37.
Fisher, J., An existence theorem for simple convex polyhedra, Discrete Math., 7 (1974) 75-97.
Fisher, J., Five-valent convex polyhedra with prescribed faces, J. Combin. Theory, Ser. A., 18 (1975) 1-11.
Goodman, J. and J. O'Rourke, Handbook of Discrete and Computational Geometry, Second Edition, Chapman & Hall/CRC, Baton Rouge, 2004.
Grinberg, E., Plane homogeneous graphs of degree three without hamiltonian circuits. Latvian Math. Yearbook 5 (1968) 51-58.
Grünbaum, B., Some analogues of Eberhard's theorem on convex polytopes, Israel J. of Math., 6 (1968) 398-411.
Grünbaum, B., Planar maps with prescribed types of vertices and faces, Mathematika, 16 (1969) 28-36.
Grünbaum, B., Polytopes, graphs, and complexes, Bull. Amer. Math. Soc., New Ser., 76 (1970) 1131-1201.
Grünbaum, B., Polytopal graphs, in Studies in Graph Theory, Part II, MAA Studies in Mathematics, Volume 12, D. Fulkerson, (ed.), Washington, 1975, p. 201-224.
Grünbaum, B., Regular polyhedra - Old and new, Aequationes Math., 16 (1977) 1-20.
Grünbaum, B., A convex polyhedron which is not equifacettable, Geombinatorics 10 (2001) 165-171.
Grünbaum, B., Convex Polytopes, 2nd. edition, Springer-Verlag, New York, 2003 (first edition, 1967, Wiley-Interscience).
Grünbaum, B. and N. Johnson, The faces of a regular-faced polyhedron, J. London Math. Society, 40 (1965) 577-86.
Grünbaum, B. and J. Malkevitch, Pairs of edge-disjoint Hamiltonian cirucits, Aequat. Maht., 14 (1976) 191-196.
Grünbaum, B. and T. Moztkin, Longest simple paths in polyhedral graphs, J. London Math. Soc., 37 (1962) 152-160.
Grünbaum, B. and T. Mozkin, On polyhedral graphs, Proc. Symp. Pure Math., Volume 7, Convexity, American Mathematical Society, Providence, 1963.
Grünbaum, G. and G. Shephard, Tilings and Patterns, W. H. Freeman, New York, 1987.
Grünbaum, B. and J. Zaks, The existence of certain planar maps, Discrete Math., 10 (1974) 93-115.
Haussner, R., Abhandlungen über die regelmäßigen Sternkörper, Ostwald's Klassiker de Exakten Wissenschaften, Nr. 151, Wilhem Engelmann, Leipzig, 1906.
Hilton, P. and J. Pedersen, Descartes, Euler, Poincaré, Pólya and Polyhedra, L'Enseignement Mathématique, 27 (1981) 327-343.
Ivanco, I. and S. Jendrol', On an Eberhard-type problem in cubic polyhedral graphs having Petrie and Hamiltonian cycles, Tatra Mt. Math. Publ., 18 (1999) 57-62.
Jeong, D., Realizations with a cut-through Eulerian circuit, Discrete Math., 137 (1995) 265-275.
Jendrol', S., A new proof of Eberhard's theorem, Acata Fac. Univ. Math., 31 (1975) 1-9.
Jendrol', S., On the face-vectors of trivalent convex polyhedra, Math. Slovaca 33 (1983) 165-180.
Jendrol', S., On face vectors and vertex vectors of convex polyhedra, Discrete Math., 118 (1993) 119-144.
Joffe, P., Some Properties of 3-Polytopal Graphs, Doctoral Thesis, City University of New York, 1982.
Johnson, N., Convex polyhedra with regular faces, Can. J. Math., 18 (1966) 169-200.
Jucovic, E., On the number of hexagons in a map, J. Combinatorial Theory, Series B, 10 (1971) 232-236.
Jucovic, E., On the face vector of a 4-valent 3-polytope, Studia Sci. Math. Hungar., 8 (1973) 53-57.
Kalai, G., A simple way to tell a simple polytope from its graph, J. Combin. Theory, Ser. A., 49 (1988) 381-383.
Kalai, G. and G. Ziegler, (eds.), Polytopes - Combinatorics and Computation, Volume 29 of DMV Seminars, Birkhäuser, Basel, 2000.
Klee, V., The Euler characteristic in combinatorial geometry, Amer. Math. Monthly, 70 (1963) 119-127.
Lakatos, I., Proofs and Refutations, Cambridge U. Press, New York 1976.
Legendre, A., Élements de géometrie, Firmin Didot, Paris, 1794.
Lebesgue, H., Remarques sur les deux premières demonstrations du théorèm d'Euler, rélatif aux polyèdres, Bulletin de la Socièté Mathématique de France, 52 (1924) 315-336.
Lebesgue, H., Quelques conséquences simples de la formule d'Euler, J. de Mathématiques pures et appliquées, Neuvième série, 19 (1940) 27-43.
L'Huilier, S., Démonstration immédiate d'un théorème est susceptible, Mém. Acad. Imp. Sci. St. Pétersb., 4 (1811) 271-301.
L'Huilier, S., Mémoire sur la Polyédrométrie, Annales de Mathématiques, 3 (1812-1813) 169-189.
Malkevitch, J., Properties of planar graphs with uniform vertex and face structure, Memoir 99, American Mathematical Society, Providence, 1970.
Malkevitch, J., Spanning trees in polytopal graphs, in Second International Conference on Combinatorial Mathematics, L. Gewirtz, L. Quintas, (eds.), Annals of the New York Academy of Sciences, Vol. 313, 1979, p. 362-367.
Malkevitch, J., The First Proof of Euler's Theorem, Mitteilungen, Mathematisches Seminar, Universität Giessen, 165 (1986) 77-82.
Malkevitch, J., Polytopal graphs, in Selected Topics in Graph Theory 3, L. Beineke and R. Wilson, (eds)., Academic Press, London, 1988, p. 169-188.
McMullen, P., On simple polytopes, Inventions Math., 113 (1993) 419-444.
McMullen, P. and E. Schulte, Abstract Regular Polytopes, Cambridge U. Press, London, 2002.
McMullen, P., and G. Shepard, Convex Polytopes and the Upper Bound Conjecture, Lecture Notes Series, Volumne 3, London Mathematical Society, Cambridge U. Press, London, 1971.
Mohar, B. and C. Thomassen, Graphs on Surfaces, Johns Hopkins U. Press, Baltimore, 2001.
Motzkin, T., The evenness of the number of edges of a polyhedron, Proc. Nat. Acad. Sciences, USA, 52 (1964) 44-45.
Robertson, N. and D. Sanders, P. Seymour, R. Thomas, The four-colour theorem, J. Combin. Theory, Ser. B, 70 (1997) 2-44.
Poinsot, L., Sur les polygones and les polyèdres, J. École Polytech., 4 (cahier 10) (1810) 16-48.
Rademacher, H. and O. Toeplitz, The Enjoyment of Mathematics, Princeton U. Press, Princeton, 1957. (Translation of the German edition of 1929, by H. Zuckerman.)
Rajwade, A., Convex Polyhedra with Regularity Conditions and Hilbert's Third Problem, Hindustan Book Agency, New Delhi, 2001.
Read, R. and R. Wilson, An Atlas of Graphs, Clarendon Press, Oxford, 1998.
Senechal, M. and G. Fleck, (eds.), Shaping Space, Birkhäuser Boston, Boston, 1988.
Shephard, G., Combinatorial properties associated with zonotopes, Canadian J. Math., 26 (1974) 302-321.
Shephard, G., Convex polytopes with convex nets, Math. Proc. Cambridge Phil. Soc., 78 (1975) 389-403.
Steinitz, E., Über die Eulerschen Polyederrelationen, Archiv. für Mathematik und Physik, 11 (1906) 86-88.
Steinitz, E. and H. Rademacher, Vorlesungen über die Theorie der Polyeder, Springer-Verlag, Belin, 1934, reprinted, Springer-Verlag, 1976.
Thomassen, C., Planarity and duality of finite and infinite graphs, J. Combin. Theory Ser. B, 29 (1980) 244-271.
Thomassen, C., Kuratowski's theorem, J. Graph Theory, 5 (1981) 225-241.
Thomassen, C., Plane representations of graphs, in "Progress in Graph Theory," J. Bondy and U. Murty, (eds.), Academic Press, New York, 1984, p. 43-69.
Thomassen, C., A refinement of Kuratowski's theorem, J. Combin. Theory Ser. B, 37 (1984) 245-253.
Thomassen, C., Rectilinear drawings of graphs, J. Graph Theory, 12 (1988) 335-341.
Thomassen, C., The graph genus problem is NP-complete, J. Algorithms, 10 (1989) 568-576.
Thomassen, C., A link between the Jordan Curve Theorem and the Kuratowski planarity criterion, Amer. Math. Monthly, 97 (1990) 216-218.
Thomassen, C., Every planar graph is 5-choosable, J. Combin. Theory Ser. B, 62 (1994) 180-181.
Thomassen, C., Trees in triangulations, J. Combin. Theory Ser. B, 60 (1994) 56-62.
Thomassen, C., 3-list coloring planar graphs of girth 5, J. Combin. Theory Ser. B, 64 (1995) 101-107.
Tutte, W., Convex representation of graphs, Proc. London Math. Soc., 10 (1960) 474-483.
Von Staudt, G., Geometrie der Lage, Nürenberg, 1847.
West, D., Introduction to Graph Theory, (Second Edition), Prentice-Hall, Upper Saddle River, 2001.
Wilson, R., Graphs, Colourings and the Four-colour Theorem, Oxford U. Press, Oxford, 2002.
Zaks, J., Non-Hamiltonian simple planar graphs, Ann. Discrete Math., 12 (1982) 255-263.
Ziegler, G., Lectures on Polytopes, Springer-Verlag, 1995.
Zitnik, A., Discrete Math., Plane graphs with Eulerian Petrie walks, 244 (2002) 539-549.
Those who can access JSTOR can find some of the papers mentioned above there. For those with access, the American Mathematical Society's MathSciNet can be used to get additional bibliographic information and reviews of some these materials. Some of the items above can be accessed via the ACM Portal , which also provides bibliographic services.







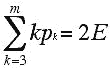 (*)
(*)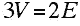
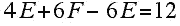
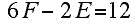 (**)
(**)
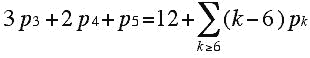 (***)
(***)




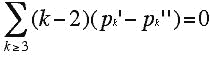

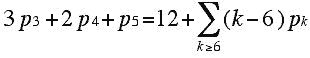 (***)
(***)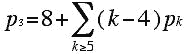 (****)
(****)