Finite-dimensional Feynman Diagrams
Feature Column Archive
4. Wick's Theorem
Calculating high-order derivatives of a function like  can be very messy. A useful theorem reduces the calculationto combinatorics.
can be very messy. A useful theorem reduces the calculationto combinatorics.
Wick's theorem
where the sum is taken over all pairings 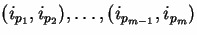 of i1, ..., im
of i1, ..., im
Wick's theorem is proved (a careful counting argument) in texts onQuantum Field Theory. The most detailed explanation is in S. S. Schweber,An Introduction to Relativistic Quantum Field Theory, Evanston, IL,Row, Peterson 1961.
Let us calculate a couple of examples.
To begin, it is useful to write  with
with 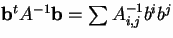 (the sums running from 1 to d)using the series expansion exp x = 1 + x +x2/2 +x3/3! ... .The typical termwill be
(the sums running from 1 to d)using the series expansion exp x = 1 + x +x2/2 +x3/3! ... .The typical termwill be  . This term is a homogeneous polynomialin the bi of degree 2n
. This term is a homogeneous polynomialin the bi of degree 2n
Differentiating ktimes a homogeneous polynomialof degree 2nand evaluating at zero will give zero unless k = 2n. So the job is to analyzethe result of 2ndifferentiations on  .
.
The differentiation carried out most frequently in these calculations is
where we use the symmetry of the matrix A-1,a direct consequence of the symmetry of A.
In what follows 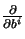 will be abbreviated as
will be abbreviated as 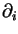 .
.
Note that (1,2) and (2,1) count as the same pairing.
Welcome to the
Feature Column!
These web essays are designed for those who have already discovered the joys of mathematics as well as for those who may be uncomfortable with mathematics.
Read more . . .
Feature Column at a glance



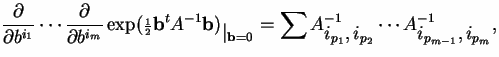

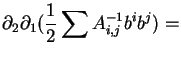
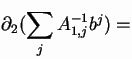 A-11,2,
A-11,2,