Informal Geometry Glossary
Connected graph
A
graph is connected if it is possible to walk along edges between any two vertices in the graph.
A connected graph is in one piece. If a graph has several pieces it is called disconnected and each piece is called a component of the graph.
Below: G is a connected graph, while H is a graph with 4 components.
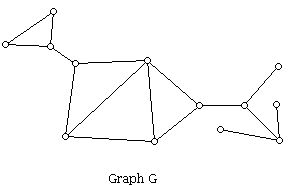
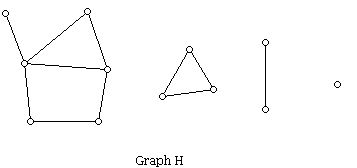 Convex
Convex
A set of points is convex if the line segment joining any two points of the set lies totally in the set.
Intuitively, sets fail to be convex because they have either notches or holes.
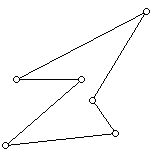
(The polygon above has two notches and is non-convex.)
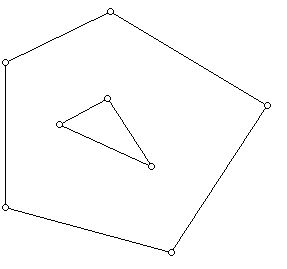
(The region lying between the pentagon and the triangle is non-convex since the region has a hole in it.)
Graph
A graph is a geometric diagram consisting of a finite collection of dots called vertices and a finite collection of line segments (which can be straight or curved) joining these dots called edges. Sometimes the definition of graph prohibits joining a vertex to itself with a line segment (i.e. loops are not allowed) and joining two distinct vertices with more than one edge (i.e. multiple edges are not allowed). If loops and edges are allowed, then a graph which lacks them is referred to as a simple graph.
Examples of simple graphs are shown below:
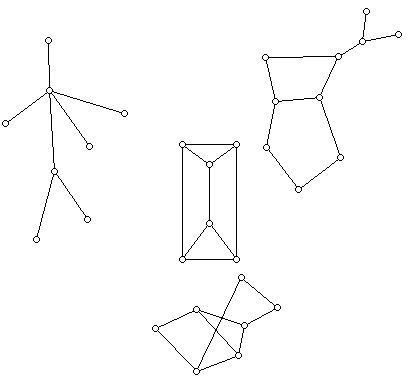
Notice that in the bottom graph there are only 7 vertices and one of the edges cuts two other edges in points that are not vertices of the graph.
Quadrilateral
A
polygon which has 4 sides is sometimes called a 4-gon.
Quadrilaterals can be either convex or non-convex. Furthermore, there are many special kinds of quadrilaterals one can mention: parallelograms, rhombuses, squares, rectangles, trapezoids, etc.
Polygon
A polygon is an alternating sequence of points (called the vertices of the polygon) and line segments (called the edges or sides of the polygon) where the last segment has an endpoint coinciding with the first point in the sequence. We do not allow these line segments to pass through previous vertices of the polygon. However, the line segments are allowed to intersect each other at points other than the vertices. Polygons where this does not happen are known as simple. Usually we insist that the whole structure lies in a single plane. A polygon with n vertices is called an n-gon. The names triangle, quadrilateral, pentagon, and hexagon are used to describe polygons with 3-6 edges, respectively.
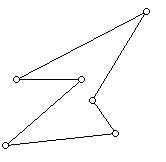
The diagram below shows a 6-gon or hexagon. This hexagon is not convex.
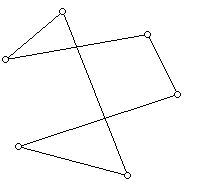
The diagram below shows a non-simple hexagon.
If all the edges of a polygon have the same length the polygon is called equilateral. If the angles between consecutive sides of a polygon are the same then the polygon is called equiangular. A polygon which is both equiangular and equilateral is called regular. Note that rectangles are equiangular but they do not have to be equilateral.
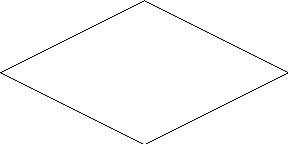
The 4-gon below is equiangular but not equilateral.

The 4-gon below is equilateral but not equiangular:
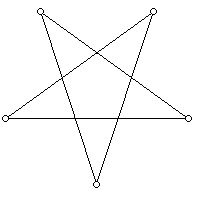
The diagram below shows a non-simple but regular pentagon:
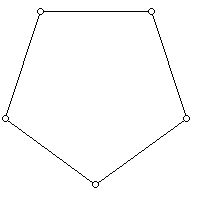
The diagram below shows a convex regular pentagon:
 Polyhedron
Polyhedron
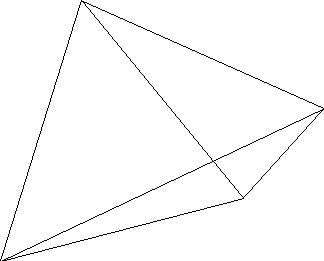
A polyhedron is a surface made up of a finite number of flat (plane) pieces. Some polyhedra may go off to infinity and others are bounded, that is, they will fit inside a large sphere. A tetrahedron is an example of a bounded polyhedron,
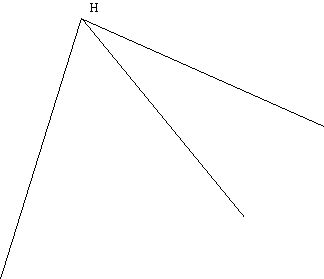
The diagram below shows an example of an unbounded polyhedron. The three rays that emanate from H go off to “infinity.”
The most familiar polyhedra in 3-dimensional space are those where the flat pieces do not intersect each other and where the surface formed is like a sphere. Such polyhedra can be either convex or non-convex. Branko Grünbaum introduced the word polytope to mean a bounded convex polyhedron.
Polyhedra exist in spaces of all dimensions. Thus, one can speak of polyhedra in 3-space or 18-dimensional space. The analog of a polyhedron in 2-dimensions is a polygon; it is made up of line segments.
Sometimes it is convenient to think of a polyhedron as a “solid,” that is, it includes the points both on the surface and the interior of the surface. However, usually when one refers to a polyhedron one means the surface itself, and if one wants to make note of the points within the polyhedron, one refers to the polyhedron and its interior.
Three-dimensional polyhedra can be thought of as being assembled from two-dimensional polygons. These polygons are referred to as the faces of the polyhedron.
Regular polygon
A
polygon is regular if it is both equiangular (all angles equal) and equilateral (all edges equal length).
Rhombus
A quadrilateral which has 4 equal length sides. A square is a special kind of rhombus which has a right angle.
Spanning tree
A spanning tree T of a graph G is a subgraph of the graph G which includes all its vertices and is a tree.
In the diagram below, the graph G is shown and a spanning tree is shown in thick red lines.
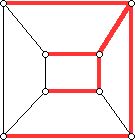
If a graph G has |V| vertices, then the number of edges in any spanning tree of G is |V| -1.
Tree
A tree is a connected graph which has no circuits.
A sample of five trees is shown below:
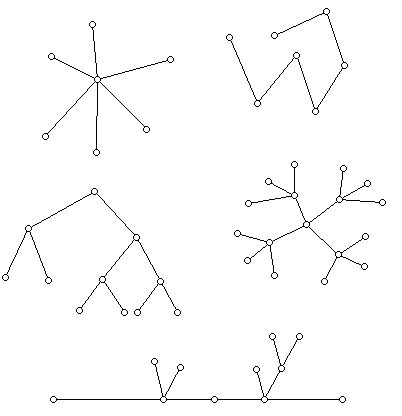
Trees have many nice properties:
There are unique paths between any two vertices.
The number of vertices is one more than the number of edges.
The removal of an edge disconnects the tree.
A tree with at least one edge contains at least two vertices of valence 1.
Valence
The valence of a vertex in a simple graph is the number of edges at the vertex. If a graph has loops, the loop contributes 2 to the valence of the vertex.
For the (simple) graph below: vertices c and e have valence 1, vertex g has valence 2, vertices a, b, and f have valence 3, and vertex d has valence 5.
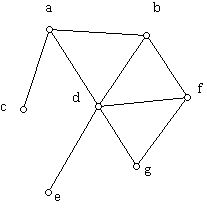
Another name for the valence of a vertex is the degree of a vertex. Computer scientists usually call vertices of a tree which are 1-valent “leaves.”


















