Gray Codes
Posted September 2008.
What can we learn from a mathematical point of view from the kinds of examples we are considering, listing mathematical objects in a list in such a way that adjacent objects in the list are close to each other?...
Joseph Malkevitch
York College (CUNY)
malkevitch at york.cuny.edu
Counting permutations
How many ways are there to take three letters a, b, c and arrange them in different ordered strings?
abc
acb
bac
bca
cab
cba
The list above shows all of the six possible different strings. The strings are listed the way they would be in a dictionary, where words that start with a come before those that start with b, and these in turn come before those that start with c. Which word, able or alert, comes first in the dictionary? Since both words start with a we have a tie, so we look at the letter in the second position. Since b comes before l, we list able before alert. This approach to ordering strings is known as lexicographical ordering. It begins with a system for an ordering of alphabetical strings of length 1 and extends to order strings of any length. Note that to carry such a process one has to know the "ordering" for the letters in the alphabet. Thus, if one has the four-symbol "alphabet" a, A, b, B, one might want to consider the lexicographical order for these 4 symbols to be a, b, A, B or a, A, b, B. Using the ordering a, A, b, B, the legicographical ordering of strings of symbols of length two without repeats would be:
aA
ab
aB
Aa
Ab
AB
ba
bA
bB
Ba
BA
Bb
while with the ordering a, b, A, B we would have:
ab
aA
aB
ba
bA
bB
Aa
Ab
AB
Ba
Bb
BA
Mathematics often involves giving precise definitions of terminology and looking at the consequences of those definitions subject to various rules. Often this offers novel approaches to objects that one thought were familiar territory.
Part of the interest in enumerating the starting collection of strings, which can be thought of as the permutations of three symbols--all the different ways to arrange three symbols where order matters--is because there are so many different situations where they arise. For example, there are 6 different ballots that a voter can produce when three candidates are ranked without ties. Alternatively, these strings are the different "passwords" or "pins" that can be created with exactly 3 fixed letters, where no letter can be repeated.
Distance between strings
However, there is a different point of view about this list of strings. We can ask if there is some way to measure how much alike or different the two strings are. We can try to determine a distance between strings. If two strings have the same length, we can find the Hamming distance between the two strings. The name for this distance honors the American mathematician Richard Hamming.
 (Richard Hamming)
(Richard Hamming)
Hamming distance is the number of "columns" (positions) the two strings differ in, if the strings appear one on top of the other. Thus, bleak and sneak differ in two positions. To see this more clearly, here are the words arranged one above the other:
sneak
bleak
The two strings differ in columns one and two, so they have Hamming distance 2.
If we compute the Hamming distance between the consecutive rows of our initial list and, when we get to the bottom of the list, think of the list as "cyclic," that is, returning to the start, or first row, and compute that Hamming distance as well, we get the total sum of distances between rows of 15.
Is this the smallest possible total that can be obtained? No!
Since the strings have distinct symbols, the smallest number of changes between two consecutive strings must be 2. In the sequence list below, the Hamming distance between two consecutive strings, including the first and last string, is two. Hence, this must be an ordering where the sum of the consecutive distances (including the top and bottom strings) is a minimum. The minimum value is 12.
abc
bac
bca
cba
cab
acb
Hamiltonian circuits
We can get a different insight here by using some graph theory, a geometric tool involving drawing pictures with dots and lines. We will represent each string of length 3 by a vertex (dot) of the graph and join two vertices by a line segment (edge) if and only if the strings differ in exactly two positions.
This graph has exactly 6 vertices and is quite symmetric because of the way it is defined. All of the vertices have exactly 3 edges at a vertex (that is, they are 3-valent). It turns out this graph is isomorphic to the graph K3,3, the complete bipartite graph with 3 vertices. (We have two sets of size three, and there are edges from each vertex in one of the sets to all of the vertices in the other set.) This graph turns out to be one of the two graphs whose "presence" in a graph prevents the graph from being embedded (drawn) in the plane so that edges meet only at vertices. The location in the "center" of the hexagonal region in Figure 1, where three edges appear to meet, is not a vertex of the graph which has been drawn. This intersection point arises by "accident" as a consequence of the way the graph has been drawn on a flat surface.
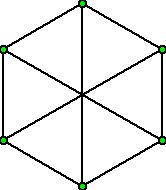 Figure 1
Figure 1
In the graph theory context, the sequence of triples we found above, which minimizes the total Hamming distance when they are listed in "cyclic order," corresponds to the fact that there is a tour of the vertices of the graph in Figure 1 which starts and ends at the same vertex and visits each vertex once and only once. Such a tour is known as a Hamiltonian circuit. William Rowan Hamilton called attention to this concept, though as often is the case, he appears not to have been the first to do so.
 (William Rowan Hamilton)
(William Rowan Hamilton)
Earlier than Hamilton the British cleric Thomas Penyngton Kirkman wrote on the topic of what has now come to be called graph theory and discussed the concept of finding a circuit of vertices in a graph which visited each vertex once and only once.
 (Thomas Penyngton Kirkman)
(Thomas Penyngton Kirkman)
The fact that Kirkman contributed to mathematics without earning his living by doing mathematics illustrates something that is true to the present day. One can enjoy and contribute to mathematics as an "amateur" if one has the interest, time and passion.
Returning to the issue of listing all the triples on three symbols from the point of view of ordering triples so as to minimize the total Hamming distance when moving cyclically from one trip to the next, I have drawn in Figures 2, 3, and 4 some Hamiltonian circuits of the graph which appears in Figure 1. These Hamiltonian circuits use different edges of the graph in Figure 1 but it is natural to ask if there is a symmetry of the graph in Figure 1 which will transform one of these Hamiltonian circuits into another.
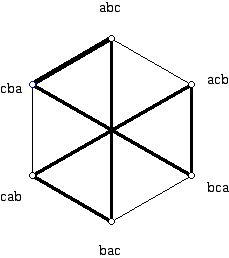 Figure 2
Figure 2
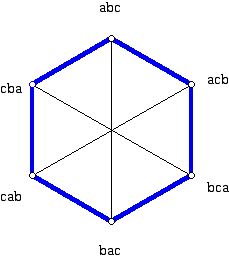 Figure 3
Figure 3
 Figure 4
Figure 4
To make the point clearer, in Figures 5, 6, and 7 of the same graph below, the Hamiltonian circuits in the first two can be thought of as the same, even though they use different edges. However, the Hamiltonian circuits in the second and third are considered different, for reasons other than that they have different edges.
 Figure 5
Figure 5
 Figure 6
Figure 6
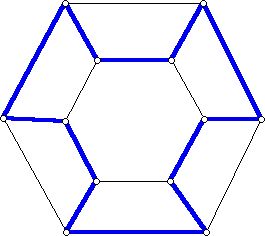 Figure 7
Figure 7
Gray codes
What can we learn from a mathematical point of view from the kinds of examples we have been considering, listing mathematical objects in a list in such a way that adjacent objects in the list are close to each other?
There are many combinatorial objects for which it is interesting to enumerate (find the total count) and then write them down in some systematic and efficient way. Problems of this kind are now sometimes referred to as "Gray Code" problems. This comes from a particular exciting and interesting example of this kind of problem, and is the one in which the notation was originally developed.
What are the binary strings of length n which differ in exactly one position? Clearly, one can think of these as the coordinates of the vertices of a d-dimensional cube. In the diagram below, showing a fairly traditional view on a piece of paper of a 3-dimensional cube, the face of the cube at the bottom has all of its third coordinates 0 while the face on the top has all its first coordinates 1. It is easy to verify that this diagram has as its coordinate strings all binary sequences of length 3.
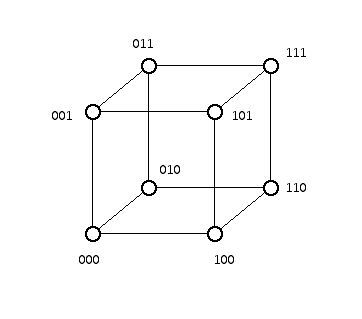 Figure 8
Figure 8
If one wants to obtain a 4-dimensional cube, one can paste together two copies of a 3-cube by adding line segments between corresponding vertices. One can add zeros to the strings in the 4th position for one of the two copies and ones for the other copy in the fourth position. This will guarantee that one gets all strings of length 4 and that all the new strings are distinct. Can you see how to label the two component cubes of the 4-cube in Figure 9 with the sixteen binary sequences of length 4 so that each pair of vertices joined by an edge has Hamming distance 1?
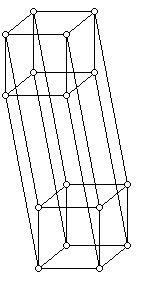 Figure 9
Figure 9
To find a cyclic list of the binary sequences of length n in which consecutive entries in the list differ in only one position, find a Hamiltonian circuit in the graph of the n-cube. It is not difficult to see that such a Hamiltonian circuit exists because we can use the idea that made it possible to construct an n-cube by joining corresponding vertices of two (n-1) cubes.
The notion of arranging a collection of objects (e.g. sequences, trees, partitions) in a cyclic order in such a manner that the number of changes to go between consecutive objects in the sequence is a minimum has come to be known as a "Gray code." The name refers to Frank Gray, an engineer who spent a sizable part of his career at Bell Laboratories. Workers at Bell Labs, although often not themselves "mathematicians," have made many important contributions to mathematics. Gray received a doctorate degree from the University of Wisconsin (Madison) in 1916, and before his involvement with Bell Labs worked for the Western Electric Company. In addition to his work on the codes which bear his name, Gray (pictured below) also was a pioneer in the development of television.
Gray in fact obtained a patent (granted in 1953 but applied for considerably earlier) for ideas involving his code which minimized the number of changes for a cyclic listing of the binary strings of length n. The code that he developed is often now referred to as the reflected Gray code.
Here is a description of how this works. Suppose one wants to construct the reflected Gray code for strings of binary sequences of length n, where one already has a solution for strings of order n-1 in the reflected Gray code form. Gray gave a construction to do this. The idea is to take the solution for (n-1) and add a 0 to all the strings on the left (as a prefix). Now take the strings and list them in reverse order but preface each with a 1.
For strings of length 1, we have the strings:
0 and 1
Note that these strings listed in reverse are 1 and 0.
Placing a zero in front of 0 and 1 we get 00, 01, and a 1 in front of 1 and 0 we get 11 and 10. Thus, we get the four strings:
00
01
11
10
Note the one-digit change between each row and between the last row and the first row. Below (Figure 10) you can see how to visualize what is going on using a Hamiltonian circuit on the 2-cube.
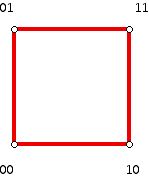 Figure 10
Figure 10
Here is another iteration of the process: We have the strings:
00, 01, 11, and 10 and in reverse order 10, 11, 01, 00.
Now prefix 0 prior to the first 4 strings and 1 prior to the last four:
000, 001, 011, 010 and 110, 111, 101, 100. We get a list of the 8 binary strings of length 3. Again, we can interpret this as a Hamiltonian circuit on a 3-cube (Figure 11).
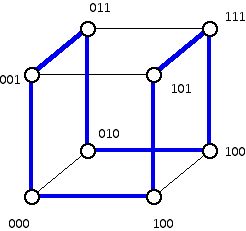 Figure 11
Figure 11
There are other Hamiltonian circuits on the 3-cube such as the one below (Figure 12) which shows an alternative ordering of the binary sequence of length 3 which can serve as a Gray code.
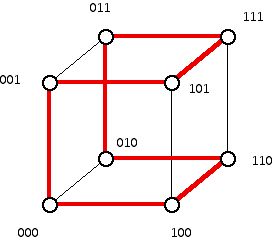 Figure 12
Figure 12
Once the mathematics community became aware of the spirit of a Gray code problem (i.e. given a collection of objects X, list them in a fashion where the total "distance" between moving between consecutive items in X so that the sum of the distances between the items arranged in a cyclic sequence is small as possible), researchers began looking for:
a. Gray codes for other combinatorial objects besides binary sequences of length n
b. applications of Gray codes to new settings in areas outside of mathematics.
Among the applications of Gray codes is analog-to-digital conversion, goniometers (devices for angle measurement), construction of various codes based on the Gray codes, and control mechanisms in communications theory.
Moving mathematical ideas into a new domain comes along relatively rarely, and deep ideas that are simple to explain are more rare. However, this does not mean that people who transfer an innovative new idea into an allied area or new area get "free lunch." As a new idea is applied in additional settings, the problems attacked often become more and more difficult and variations evolve which are very challenging. Such is the case with Gray code problems.
We know that the number of binary sequences of length n is 2n. Furthermore, if we construct a graph whose vertices represent binary sequences and where vertices are joined by an edge if they are Hamming distance one apart, we get a very elegant object, namely the n-cube. However, many Gray code problems "live" in a more subtle environment.
For example, let us consider another fascinating circle of ideas, this time from the domain of number theory. Suppose we are given a positive integer n, say for example 4. What are the ways of writing 4 as the sum of one or more positive integers? For 4, a list of such choices appears below:
4
3, 1
2, 2
2, 1, 1
1, 1, 1, 1
Note that we are not interested in considering different arrangements of the terms making up the "list" as different, and hence, 2, 1, 1 is considered the same as 1, 2, 1. The numbers such as 3 and 1 are known as a partition of 4, and the list above enumerates all of the partitions of 4. These partitions are listed with largest part first down to the smallest part. Note that if one regards this as a cyclic sequence there is a "large distance" between the number of parts in row 1 and the number of parts in row 5. Note also that we cannot use Hamming distance here to find the distance between two rows because the strings in the different rows need not have the same length and Hamming distance can only be used for strings that have the same length. (However, there is a way to enumerate the partitions of n in a way that makes the listing into a Gray code problem.) Using ideas related to the partitions of the number 4, the geometer Branko Grünbaum was able to find a novel way of classifying convex plane quadrilaterals which has led to a variety of new directions for problems in elementary geometry.
Innovative mathematical ideas have a life of their own. Frank Gray's ideas about how to code binary sequences is but one of many examples.
References:
Barnes, T. and C. Savage, Efficient generation of graphical partitions, Discrete Applied Math., 78 (1997) 17-26.
Bhat, G. and C. Savage, Balanced Gray codes, Electronic J. Comb., 3 (1996).
Buck, M. and D. Wiedemann, Gray codes and restricted density, Discrete Math., 48 (1984) 19-29.
Chang, C. and R. Lee, M. Du, Symbolic Gray code as a perfect multiattribute hashing scheme for partial match queries, IEEE Trans. Software Eng., 8 (1982) 235-249.
Etzion, T. and K. Patterson, Near optimal single track Gray codes, IEEE Trans. on Information Theory, 42 (1996) 779-789.
Flajolet, P. and L. Ramshaw, A note on Gray code and odd-even merge, SIAM J. Comput., 9 (1980) 142-158.
Fredman, M., Observations on the complexity of generating quasi-Gray Codes, SIAM J. Comput., 7 (1978) 134-146.
Gilbert, E., Gray codes and paths on the n-cube, Bell System Tech. J., 37 (1958) 815-826.
Grünbaum, B., The angle-side reciprocity of quadrangles, Geombinatorics, 4 (1995) 115-118.
Hamming, R., Coding and Information Theory, Prentice-Hall, Englewood Cliffs, N.J., 1980.
Joichi, J. and D. White, Gray codes in graphs of subsets, Discrete Math., 31 (1980) 29-41.
Joichi, and D. White, S. Williamson, Combinatorial Gray codes, SIAM J. Comput., 9 (1980) 130-141.
Kaye, R., a Gray code for set partitions, Inform. Process. Lett., 5 (1976) 171-173.
Killian, C. and C. Savage, Antipodal Gray codes, Discrete Math., 281 (2004) 221-236.
Klingsberg, P., a Gray code for compositions, J. Algorithms, 3 (1982) 41-44.
Luneberg, H., Abh. Math. Sem. Univ. Hamburg, 52 (1982) 208-227.
Prodinger, Nonrepetitive sequences and Gray code, Discrete Math., 43 (1983) 113-116.
Proskurowski, A. and Frank Ruskey, Binary tree Gray codes, J. Algorithms, 6 (1985) 225-238.
Ruskey, F. and T. Hu, Generating binary trees lexicographically, SIAM J. Comput., 6, (1977) 745-758.
Ruskey, F. and C. Savage, Gray codes for set partitions and restricted growth tails, Australasian J. of Comb., 10 (1994) 85-96.
Ruskey, F. and C. Savage, A Gray code for combinations of a multiset, European J. of Combinatorics, 17 (1996) 493-500.
Ruskey, F. and C. Savage, T. Wang, Generating necklaces, J. of Algorithms, 13 (1992) 414-430.
Savage, C., Gray code sequences of partitions, J. of Algorithms, 10 (1989) 577-595.
Savage, C., Generating permutations with k-differences, SIAM J. Discrete Math., 3 (1990) 561-573.
Savage, C., A survey of combinatorial gray codes, 39 (1997) 605-629.
Sedgewick, R., Permutation generation methods, Computing Surveys, 9 (1977) 137-164.
Shama, B. and R. Khanna, On m-ary Gray codes, Inform. Sci., 15 (1978) 31-43.
Slater, P., Generating all permutations by graphical transpositions, Ars Combinatoria, 5 (1978) 219-225.
Suparata, I. and A. Van Zanten, A construction of Gray codes inducing complete graphs, Discrete Math. 308 (2008)
Wang, M., An algorithm for Gray-to-binary conversion, IEEE Trans. Computers, 15 (1966) 659-660.
Wilf, H. Combinatorial Algorithms, SIAM, Philadelphia, 1989.
Yuen, C., The separability of Gray codes, IEEE Trans. Inform. Theory, 20 (1974) 668.
Joseph Malkevitch
York College (CUNY)
malkevitch at york.cuny.edu
Those who can access JSTOR can find some of the papers mentioned above there. For those with access, the American Mathematical Society's MathSciNet can be used to get additional bibliographic information and reviews of some these materials. Some of the items above can be accessed via the ACM Portal , which also provides bibliographic services.





















