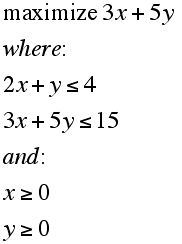People Making a Difference
Posted January 2009.
Klee contributed to combinatorics, convexity, algorithms, and optimization problems but his work always had a strongly geometric flavor....
Joseph Malkevitch
York College (CUNY)
malkevitch at york.cuny.edu
Introduction
Mathematics has a reputation as a subject of austere beauty - a subject that resonates for some people the way that a beautiful sunrise or sunset, a beautiful symphony, or a beautiful painting might for other people. Yet mathematics also has its applied side. Without mathematics that was developed in the 20th century we would not have the cell phones that are radically changing the way we live our lives in the early 21st century. Against a backdrop of the dual aspects of mathematics, its beauty and applicability, is the sense that the frontiers of mathematics are getting further and further from what an "average person," one not pursuing a career in mathematics or one of its closely allied fields, can master. There has been an increase in the length and complexity of mathematical proofs and in some cases, important theorems have required a computer in an integral way. Examples of this are the results of Wolfgang Haken and Kenneth Appel that confirm the conjecture that every plane map can have its faces colored with 4 or fewer colors and Thomas Hale confirming the maximal density that spheres packed in 3-space can achieve.
Yet because of the work of many individual mathematicians and their passion for some parts of mathematics, as well as the clarity of their insights, based on the work of countless generations of impassioned mathematicians of the past, it is possible to see the dual aspects of mathematics' beauty and applicability more clearly. There are many such people, but here I would like to call attention to the work of the American geometer Victor Klee, who recently died.
Victor Klee was one of America's most prominent geometers.

His recent death (August 2007) is a great loss for the mathematics community. His published works included several books and over 240 research papers. Klee was born in San Francisco in 1925 and attended Pomona College with a major in both mathematics and chemistry. Whereas prior to the 20th century nearly all mathematicians (e.g. Newton, Gauss, Euler, Laplace, etc.) made contributions to not only mathematics but physics or some other branch of science, the pressures of specialization have made this more rare. Although most of Klee's work had a geometric focus, his work spanned a wide range of interests motivated by both theoretical and applied considerations. He received his doctorate degree from the University of Virginia, where he studied with the prominent topologist Edward McShane. His doctoral thesis (1949) was entitled:
Convex Sets in Linear Spaces
Klee's early training and research was in the area of topology-- the study of properties of geometric objects that go beyond the traditional concern with angles, distances, and areas of the Euclidean geometry tradition. Thus, from a topological point of view, a straight line segment and a curved segment are alike, and a square and a (Euclidean) ellipse are alike, but a segment and a circle are not alike. This topological difference means that a circle "separates" a plane into an interior region and an exterior region, while a segment does not. Thus, if one picks any two points in a plane not on a segment (or even a finite number of segments), one can find a curve which joins these two points and has no point in common with the segment. However, for a point inside a circle and one outside the circle, any curve joining the points must have a point in common with the circle. This is the kind of geometric information that interests a topologist and does not require information about distances.
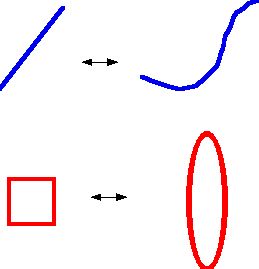 Figure 1: Geometric sets can look different but be topologically equivalent.
Figure 1: Geometric sets can look different but be topologically equivalent.
Most of Klee's career was spent at the University of Washington (Seattle) where he joined the faculty in 1953; he retired from that university in 2000. In his years at the University of Washington, Klee supervised 34 doctoral students, most of whom would describe themselves as geometers. His students in turn have trained many additional geometers. According to the Mathematics Genealogy Project, Klee has 100 mathematical descendants (and he had "regular" children and grandchildren as well). For much of the time Klee was at the University of Washington, another prominent geometer, Branko Grünbaum was also there. The joint presence of Klee and Grünbaum made the University of Washington a center for an evolving newer brand of geometry for about 30 years. From 1971-1972 Klee served as the president of the Mathematical Association of America. Klee contributed to combinatorics, convexity, algorithms, and optimization problems but his work always had a strongly geometric flavor. To fully understand the place that Victor Klee has had in the recent evolution of geometry, it is necessary to take a bit of an aside, to look ever so briefly at the evolution of geometry from ancient to modern times.
What is geometry?
During the early part of the 20th century the study of geometry was at a crossroads. During the late 19th century the world of geometry was rocked by what turned out to be one of the great milestones of intellectual history, not only from the point of view of mathematics but knowledge in general.
The backbone of the study of geometry throughout much of history has been Euclid's Elements. This book has gone through an enormous number of editions in a large array of languages almost since it was written. Although we know little about the man Euclid and have no version of this book that dates back even close to the time that Euclid lived, the Elements has been central to the evolution of geometry. The content of the Elements helped keep mathematics alive during many periods and has inspired many individual mathematicians to become mathematicians, in particular, geometers. There are many beautiful results in the Elements including a discussion of the 5 regular polyhedra and prime numbers. The seminal algorithm, known as the Euclidean Algorithm, for finding the largest positive integer that divides two positive integers can also be found there. The famous 5th postulate of Euclid is:
If a straight line falling on two straight lines makes the interior angles on the same side less than two right angles, the two straight lines, if produced indefinitely, will meet on that side on which the angles are less than the two right angles.
This seemed to many people more complex than the other axioms, and attempts were made to see if this axiom could be proved using the law of logic from the other axioms. It remained until the late 19th century to realize that these efforts were doomed. This work was done by Gauss, Bolyai, and Lobachevsky, but only the last two men published their findings. What emerged is that there are exciting geometries, usually called the "classical non-Euclidean geometries" which arise when one modifies the 5th postulate so that there are no parallels to a line m through a given point P or there are many parallels to a line through a point. One of the classical non-Euclidean geometries is projective geometry. You can think of this geometry as starting with a sphere in 3-dimensional Euclidean space. How are we to interpret the undefined terms "point" and "line" in this geometry? A point of the "new geometry" will be the identified points at the ends of diameters of the sphere, that is, if P and P* are the points at the ends of a diameter, think of (the set) {P, P*} as a single point. The lines of the "new" geometry will be the circles on the sphere whose centers coincide with the center of the sphere. It is now easy to see that with these definitions of point and line, two points determine a unique line and two lines must always intersect at a point, and, thus, we have a geometry without parallel lines.
The diagram below may help you visualize some aspects of the hyperbolic, or Bolyai-Lobachevsky Plane, which is the other classical non-Euclidean geometry. It is known as the Cayley-Klein Model, for the mathematicians Arthur Cayley and Felix Klein. If point and line are undefined, we can interpret these two terms as follows. A point will mean any of the points interior to a circle, such as the one shown in Figure 2. A line will mean any chord of the circle (not including the points on the boundary). Thus, a line such as m consists of the points of a chord whose endpoints lie on the circle but are "deleted" for our purposes. Now, you can see that if P is a point not on m, there are many, infinitely many chords which contain P and do not meet the chord m. Now we have infinitely many lines through a point P which are parallel to a line m which does not contain P!
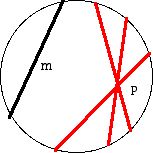
Figure 2: A model for a geometry with many lines parallel to a given line through a point.
The discovery of the non-Euclidean geometries created a kind of "crisis" in the philosophical community and that of mathematics as well. Since projective geometry and hyperbolic geometry were on an equal footing to Euclidean geometry from a mathematical point of view, the question arose what was the true geometry of physical space. Perhaps we live in a space which is not Euclidean! (In Euclidean geometry the sum of the angles of a plane triangle add to 180 degrees, while in the geometry of the sphere they add to more than 180 degrees, and in the hyperbolic plane to less than 180 degrees.) It also raised the question of what direction the study of geometry should take. Relatively speaking, the hyperbolic plane requires more sophistication for its study than is true of Euclidean geometry. Mathematics educators were faced with the question of how much attention should be given to the new geometries (there were also developments in the area of finite geometry during this period). With the publication of Hilbert's Axioms, which clarified the "oversights" that arise in Euclid and provided an independent collection of axioms (that is, none of the axioms could be proved from the others) for Euclidean geometry, geometry seemed in some ways to "run out of steam." The person who helped rejuvenate geometry during a period when doing geometry was out of fashion to some extent was the distinguished geometer Harold Scott MacDonald Coxeter.

(Harold Scott MacDonald Coxeter, known as Donald Coxeter)
Coxeter, who was recently the subject of a biography whose title included "The Man Who Saved Geometry," worked in a niche that grew out of 19th century geometry. His work emphasized the metrical (distance) and axiomatic aspects of geometry. Throughout his life he acted as a "bridge" between the geometry of the past (19th century and earlier) and the emerging new interests of geometers in the 20th century. Coxeter also made connections between geometry and algebra. In particular, he showed the power of using group theory and symmetry ideas to get insights into geometric questions. Coxeter worked on questions involving polyhedra in higher dimensions. This work concerned questions about very symmetric polyhedra that were the analogues of the famous five regular polyhedra (Platonic Solids) that had been studied by Euclid. Klee, who was 18 years younger from Coxeter, would follow very much in the "geometric tradition" but with a very different set of interests than Coxeter, in part set in place by his training in topology.
Klee's mathematics
Klee's mathematics ranged across many aspects of geometry. In what follows I would like to call attention to three important results that Klee was involved with, which can be discussed in elementary terms: Art Gallery theorems, the Klee-Minty polytopes, and Kleetopes. First, I will sample a few items which show his blend of interests in topics that touch both theoretical and applicable mathematics. He made especially important contributions to the theory of convex polytopes, notably, polytopes in higher dimensional spaces. A polytope is a bounded convex set which is the intersection of the higher dimensional analogue of planes. (Note: A set is convex when for any two points p and q in the set, the line segment joining p and q is also in the set.)
 Figure 3: Interior of a convex pentagon (left); non-convex pentagon (right)
Figure 3: Interior of a convex pentagon (left); non-convex pentagon (right)
The theory of polytopes, though a theoretical area from the point of view of theoretical mathematics, has a dramatic connection with applicable mathematics.
Linear programming
During World War II large numbers of men and vast amounts of material had to be transferred from the United States to the European and Pacific war theaters. The United States, in the throes of coming out of the Great Depression, had refitted its factories to manufacture the material of war rather than consumer products. A new sub-discipline within mathematics, variously called operations research or management science, was to emerge in the aftermath of the war. The roots of this work were laid down by the need to find mathematical tools for fighting the war successfully. (Another triumph of mathematics during the war was in breaking both German and Japanese codes.) After the War, being able to solve large problems in production management, scheduling, cost minimization, etc. became increasingly important for governments, industry, and businesses.
The cornerstone of this new branch of mathematics became known as linear programming. A typical linear programming problem might involve how to produce different types of gasoline from different kinds of crude oil. The idea is that each product requires a certain amount of the raw materials for its manufacture. Furthermore, there are certain amounts of raw materials available at different costs. The goal of the process is to minimize the cost of producing the needed amounts of gasoline from the available crude oil supplies. Similar problems can be formulated mathematically as finding the minimum or maximum value of a linear expression, subject to constraints which take the form of a linear system of inequalities. A "baby" problem of this kind, so you can see what they look like in mathematical terms, is shown below:
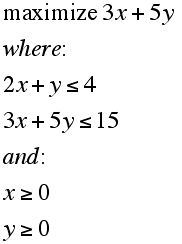
The inequalities above correspond to the interior points of a polygon in 2-dimensional space (shown in red in Figure 4, below. Can you find the coordinate of the point G?). In more general problems there are typically hundreds of variables with perhaps thousands of constraints. These questions lead to problems about the generalization of the polygon concept to higher dimensional spaces. These are the objects known as polytopes. It turns out that the points which satisfy such constraints must be the points on or inside a higher dimensional polytope. However, remarkably, it can be shown that the optimal solution of such a problem always lies at a vertex of the "feasible" polyhedron. In the diagram in Figure 4, there are 4 points to which we can restrict attention in trying to determine where the maximum value occurs among all points that satisfy the constraints. The theorem which gives this result is sometimes known as the Corner Point Theorem. Another way of putting this result is that miraculously, instead of having to check infinitely many points to see where an optimal (best) solution occurs, it is only necessary to check a finite number of points, the corners, to see where the best solution occurs.
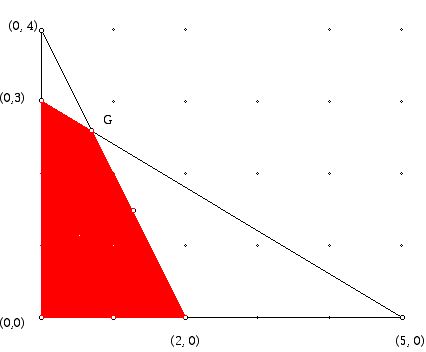
Figure 4: (The points which satisfy the contents of a linear programming problem.)
To solve large-scale linear programming problems one uses a tool known as the simplex algorithm, invented soon after the war by the American mathematician George Dantzig. The simplex algorithm made it possible to solve large-scale production, resource allocation, scheduling, and product manufacturing problems. However, though the algorithm seemed to solve very large problems in a reasonable amount of computer time, it was unclear what the theoretical complexity of the algorithm was; that is, as the size of a linear programming problem became larger and larger as measured by the number of variables and constraints it had, how much computer calculation was needed to solve these problems? The way the simplex method works is that it first locates a point which is feasible, i.e. meets the constraints specified by the problem. Suppose the linear programming problem we are trying to solve is a maximization problem. We seek the value of the variables which makes a certain linear function (known as the objective function) as large as possible. Starting at this feasible point the algorithm chooses a neighboring vertex of the feasible polyhedron, a vertex which is joined to the currently being considered vertex by an edge, which has at least as high a value for the objective function. Now one moves to that neighboring vertex and tries to find an even better neighbor, if possible. It is known that if one reaches a point where all the neighbors offer no higher value of the objective function than the current value, the current value can not be improved. (Thus, there may be several places where an optimal value can occur, but no better value than one that occurs where all neighbors of the current value offer no improvement.) Victor Klee was instrumental in helping make the connection between the applied world of linear programming and the theoretical landscape of the theory of polytopes.
He did this with his work on what are now called the Klee-Minty Polyhedra. This work was joint with George Minty. Many of Klee's papers grew out of an interest that he had in linear programming problems. As discussed above, linear programming is a discrete optimization model where the goal is to maximize or minimize a linear expression where the the values of the variables in the linear expression lie within a convex polyhedron. Since linear programming problems arise in a wide variety of situations including resource allocation, scheduling, and blending, it was of interest to know how much time it might take a computer to solve these problems using the simplex method when the problem size was very large. Despite the fast time that problems were being solved in practice, there was no theoretical result showing that the amount of work to solve these problems was less than how some polynomial would grow for large values. Klee and Minty showed, by example, that the simplex method might require an exponentially large amount of work to solve some problems. The clever idea they had was to modify the structure of a very symmetrical higher dimensional cube, say the d-cube (which has 2d vertices). For example, the diagram below shows a 4-dimension cube.

Figure 5 : Diagram of a 4-cube
By choosing a suitable distortion of the d-cube, that is, a d-cube which was combinatorially equivalent to a very symmetric (regular) cube, Klee and Minty showed that for this version of the d-cube the simplex algorithm starting at a particular point would have to move through all of the vertices of the d-cube (which is exponentially large, 2d) before reaching the vertex of the d-cube that had the optimal value of the objective function. This means that the simplex algorithm follows an edge tour that results in a "hamiltonian path" (that is, while the path goes through all the vertices of the d-cube, the first and last vertex of the path need not be joined by an edge). This family of examples is now known as the Klee-Minty cubes. The Klee-Minty examples mean that the kinds of linear programming problems that occur in practice seem not to have as feasible regions those polytopes that require exponential work since in practice the simplex algorithm runs quickly. This work, which grew out of Klee's theoretical work on the path structure of higher dimensional polyhedra, shows how theoretical and applied ideas in mathematics often complement each other. To this day there are still problems about the diameter of polytopes (e.g. how far apart can vertices of d-polytopes be) which Klee popularized and worked on, that remain unsolved.
Summarizing, what Klee and Minty did was construct a family of polyhedra which had an exponentially growing number of vertices as a function of the dimension and for which, when one applied the simplex method for solving a linear programming problem on these polyhedra, the method required that one visit all of the polyhedron's vertices before reaching the optimal value. This family of examples showed that the simplex algorithm could require an exponential amount of work. For reasons that are not totally clear, examples of real world linear programming problems do not display this kind of behavior. In practice, very large linear programming problems are typically solved very quickly using the simplex method. This makes life easier for businesses and governments around the world!
Kleetopes
Early on in the history of polyhedra, the question of whether or not a polyhedron had a simple closed circuit which included all its vertices, a hamiltonian circuit, has been of interest. Part of this interest stemmed from the fact that if a convex polyhedron with at least three edges at a vertex has a hamiltonian circuit then its faces can be colored with 4 colors. The way to see this is that the graph of an convex 3-dimensional polyhedron P can be drawn in the plane. Once one has such a "plane" drawing, if there is a hamiltonian circuit for the graph (consisting of the vertices and edges of P), then by the Jordan Curve Theorem applied to the hamiltonian circuit, there are faces on the inside of the graph and on the outside of the graph. Now one can color the interior faces with 2 colors and the exterior faces with 2 colors. A typical example is shown in the diagram below. Notice that there is a special face in this diagram, colored turquoise, that surrounds all of the other faces of the graph. The hamiltonian circuit is shown with thick black edges. The two colors used for the faces inside the hamiltonian circuit are red and green, while the faces in the exterior of the hamiltonian circuit are colored blue and turquoise.
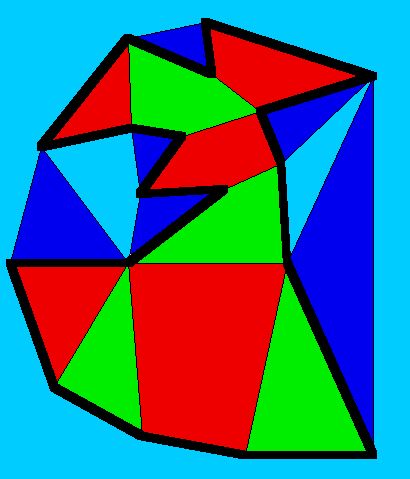
Figure 6: The regions of a graph drawn in the plane which has a hamiltonian circuit colored with 4 colors.
(It turns out that this approach to the 4-color problem will not work since there exist non-hamiltonian 3-valent polyhedra, the first such example being due to W.T. Tutte.) It was natural that Klee would have an interest in whether high dimensional polyhedra always had hamiltonian circuits. This was in part because of his keen interest in linear programming problems and theoretical questions associated with paths on polytopes. Using a very simple idea Klee showed that there existed non-hamiltonian polytopes in every dimension. His idea can be illustrated in three dimensions using the idea that has come to be called a Kleetope.
One starts with a polyhedron all of whose faces are triangles. An example of a graph of such a polyhedron is shown in Figure 7
 Figure 7: The graph of a polyhedron with all faces being triangles.
Figure 7: The graph of a polyhedron with all faces being triangles.
The graph is the graph of the regular octahedron. Note that it has 6 vertices and 8 faces. Thus, the polyhedron has more faces than vertices. What Klee did to construct a non-hamiltonian polyhedron was to erect a pyramid on every face of this polyhedron. The construction is carried out in Figure 8.
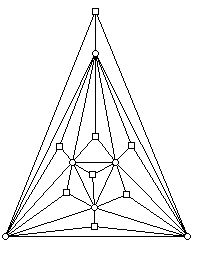 Figure 8: Pyramids drawn on all of the faces of the polyhedron in Figure 7. This new polyhedron is known as a Kleetope.
Figure 8: Pyramids drawn on all of the faces of the polyhedron in Figure 7. This new polyhedron is known as a Kleetope.
The original vertices from Figure 7 are shown with circles and the new vertices, which are the "apexes" of the pyramids, are shown as squares. Note that this graph is not a bipartite graph. (Bipartite graphs are ones where the vertices can be colored with two colors so that vertices joined by an edge get different colors.) However, square vertices are only joined to circle-labeled vertices, but circle-labeled vertices are joined to both circle-labeled vertices and square-labeled vertices. The graph above can not have a hamiltonian circuit, since to get to a square vertex, one must have come from a circle vertex, but there are not enough such vertices to form a simple circuit with the square vertices, since the initial polyhedron had more faces than vertices. The diagram above is a combinatorial diagram, and for this graph, Steinitz's Theorem guarantees the graph can be realized by a convex 3-dimensional polyhedron. However, one does not have to invoke Steinitz's Theorem for this purpose, as Klee observed. Suppose one picks a particular triangle of the polyhedron in Figure 1. If one selects a point very close to the plane that forms this face, above the interior of this face, then a "flat" pyramid over this face will not destroy the convexity of the resulting new polyhedron. This process can be carried out for each of the faces of the original polyhedron in Figure 7 in turn, until one gets a polyhedron with the same graph as the one in Figure 8.
The analogous idea can be carried out in d dimensions, where no analogue of Steinitz's Theorem is known to hold. Thus, Klee's simple idea made it possible to see how to construct non-hamiltonian convex polytopes (and their graphs) in higher dimension. This spurred interest in the question of whether or not higher dimensional polytopes with stronger properties always had hamiltonian circuits. For example, an open question of David Barnette, one of Victor Klee's doctoral students, concerns hamiltonian circuits of 4-dimensional polytopes. A convex polyhedron in d-dimensions is called simple if the valence (degree) of every one of its vertices is d. Thus, a simple convex polyhedron in 3-dimensions would have valence 3 while a simple convex polyhedron in 4-dimensions would have valence 4. While it turns out that there are non-hamiltonian simple polytopes of valence 3 in 3-dimension (the smallest example has 38 vertices), David Barnette has conjectured, and it is still an open problem, that every simple 4-dimensional convex polyhedron has a hamiltonian circuit. Klee's legacy lives on in the geometrical work of his students!
Of these three remarkable achievements, the role Klee played in the development of "art gallery" theorems is the most recent. In 1973 the young Czech mathematician Vasek Chvatál challenged Victor Klee to describe an "interesting" problem in elementary geometry. Klee responded with the following problem.
Suppose we are given a plane simple polygon with n sides. The polygon can be thought of as the floor plan of a bank, museum, or art gallery. We desire to put sensors at some of the vertices of the polygon so that collectively these sensors can see or guard all of the points in the interior of the museum. A point p in the interior of the polygon is said to be visible from a vertex v of the polygon if the line segment pv contains no points from the exterior of the polygon. (This condition is not very realistic. It means that a point p can be visible from a vertex v even if the line from v to p includes many isolated vertices or even segments from the boundary of the polygon. However, it is mathematically convenient to describe the problem this way.)
Although Klee had a conjecture that there were some n-gons that required [n/3] (n/3 rounded down, so [5/3] = 1) vertex guards, and that there are no n-gons which ever require more than [n/3] guards, he could not prove this. Chvatál gave the first proof of this conjecture, but it was Steve Fisk who provided a truly elegant way to see what was going on.
A common misunderstanding of this problem is that what is being asked for is an algorithm which finds for a given fixed polygon P what is the minimum number of vertex guards for the polygon P. This is clearly both an interesting and important problem. However, unfortunately, all known algorithms for this problem require an exponential amount of work as a function of n, the number of sides of the polygon. More precisely, it is known that this problem is NP-Complete. This means that it is unlikely that there is a polynomial time algorithm which finds the minimum number of guards for a fixed polygon P.
Victor Klee had a genius for finding simple ideas, examples, and problems that got to the very heart of geometrical and combinatorial questions. His inquiring mind has changed the direction of geometry and enriched geometry and mathematics immeasurably.
References:
Alexandrov, A., Convex Polyhedra, Springer, Heidelberg, 2005.
Brannan, D. and M. Esplen, J. Gray, Geometry, Cambridge U. Press, Cambridge, 1999.
Brondsted, A., An Introduction to Convex Polytopes, Springer-Verlag, New York, 1983.
Chvátal, V., A combinatorial theorem in plane geometry, JCT (B), 18 (1975) 39-41.
Coxeter, H., Regular Polytopes, Methuen, London, 1948.
Coxeter, H., Introduction to Geometry, Wiley, New York, 1961.
Coxeter, H., Non-Euclidean Geometry, Fifth Edition, U. of Toronto Press, Toronto, 1965.
Coxeter, H., Regular Complex Polytopes, Cambridge U. Press, London, 1974.
Coxeter, H., The Beauty of Geometry: Twelve Essays, Dover Publications, Mineola, 1999.
Coxeter, H. and B. Grünbaum, Face-transitive polyhedra with rectangular faces and icosahedral symmetry, Discrete Computational Geometry, 25 (2001) 163-172.
Fisk, S., A short proof of Chvátal's watchman theorem, JCT (B) 24 (1978) 374.
Gritzmann, P. and B. Sturmfels (eds.), Applied Geometry and Discrete Mathematics: The Victor Klee Festschrift, American Mathematical Society, Providence, 1991.
Goodman, J. and J. O'Rourke (eds.) Handbook of Discrete and Computational Geometry (second edition), Chapman & Hall/CRC, Boca Raton, 2004.
Grünbaum, B., Convex Polytopes, Wiley, New York, 1967.
Grünbaum, B., Convex Polytopes, Second edition, prepared by Volker Kaibel, Victor Klee, and Günter Ziegler, Springer, New York, 2003.
Grünbaum, B., Polytopal Graphs, in Studies in Graph Theory, Part II (D. Fulkersen, ed) MAA STudies in Mathematics, Volume 12, Mathematical Association of America, Washington, 1975.
Hadwiger, H. and H. Debrunner, V. Klee, Combinatorial Geometry in the Plane, Holt, Rinehart and Winston, New York, 1964.
Hartshorne, R., Geometry: Euclid and Beyond, Springer, New York, 2000.
Henderson, D., Experiencing Geometry, Second Edition, Prentice-Hall, Upper Saddle River, 2001.
Henderson, D. and D. Taimina, Experiencing Geometry with History, Prentice-Hall, Upper Saddle River, 2005.
Honsberger, R., Mathematical Gems II, Mathematical Association of America, Washington, 1976, p. 104-110.
Klee, V. (ed.), Convexity, Proceedings Symp. Pure Math., Volume 7. American Mathematical Society, Providence, 1963.
Klee, V., Diameters of polyhedral graphs, Canadian J. Math., 16 (1964) 602-614.
Klee, V., A property of d-polyhedral graphs, J. Math. Mechanics, 13 (1964) 1039-1042.
Klee, V. A combinatorial analogue of Poincaré's duality theorem, Canadian J. Math., 16 (1964) 517-534.
Klee, V., The number of vertices of a convex polytope, Canadian J. Math., 16 (1964) 701-720.
Klee, V., Paths on polyhedra, I., SIAM J., 13 (1965) 946-956.
Klee, V., Convex polytopes and linear programming, in Proc. IBM Scientific Computing Symposium, March 16-18, 1964, published, 1966, pp. 123-158.
Klee, V., Paths on polyhedra, II., Pacific J. Math., 17 (1966) 249-262.
Klee, V., Polytope pairs and their relationship to linear programming, Acta Math., 133 (1974) 1-25.
Klee, V. and G. J. Minty. How good is the simplex algorithm? In O. Sisha, editor, Inequalities III, pages 159--175. Academic Press, 1972.
Klee V. and S. Wagon, Old and New Unsolved Problems in Plane Geometry and Number Theory, Mathematical Association of America, Washington, 1991.
Klee, V. and D. Walkup, the d-step conjecture for polyhedra of dimension d < 6, Acta Math., 133 (1967) 53-78.
Malkevitch, J. (ed.) Geometry's Future (Second edition), Consortium for Mathematics and Its Applications, Bedford, 1991.
Meisters, G., Polygons have ears, Amer. Math. Monthly 82 (1975) 648-651.
O'Rourke, J., Art Gallery Theorems and Algorithms, Oxford U. Press, New York, 1987.
Pritchard, C. (ed.), The Changing Shape of Geometry, Cambridge U. Press, Cambridge, 2003.
Roberts, S., King of Infinite Space: Donald Coxeter, the Man Who Saved Geometry, Walker, New York 2006.
Stahl, S., The Poincaré Half-Plane, Jones and Bartlett, Boston, 1993.
Ziegler, G. Lectures on Polytopes, Springer-Verlag, New York, 1995.
Joseph Malkevitch
York College (CUNY)
malkevitch at york.cuny.edu
Those who can access JSTOR can find some of the papers mentioned above there. For those with access, the American Mathematical Society's MathSciNet can be used to get additional bibliographic information and reviews of some these materials. Some of the items above can be accessed via the ACM Portal , which also provides bibliographic services.