Mathematical Marriages
Posted November 2004.
These theorems involve such intuitively appealing yet deep ideas that they serve as a metaphor for the marriage of the emotional and intellectual, examples of mathematics at its most transcendent.
Joseph Malkevitch
York College (CUNY)
malkevitch at york.cuny.edu
1. Introduction
Marriages are a time for high spirits, celebration, and warm feelings. Mathematics has a reputation of being an impersonal subject, with austere pleasures rather than a subject of high emotion or celebration. Yet, there is a body of mathematical results known as marriage theorems. Why marriage theorems? One reason is the playfulness and whimsey of mathematicians, who enjoy spinning out seemingly artificial tales and giving these tales names forming analogies or connections with everyday experiences. The other is that perhaps by serendipity, two of mathematics' marriage theorems are causes for celebration, high spirits, and warm feelings. These theorems involve such intuitively appealing yet deep ideas that they serve as a metaphor for the marriage of the emotional and intellectual, examples of mathematics at its most transcendent. The unexpected dividend in both cases is that ideas born of theoretical mathematics have shown many applied directions.
2. Philip Hall's Marriage Theorem
Suppose that one has a collection of men and women. Each man knows exactly k women and each woman knows exactly k men. Is it possible to marry off everyone so that in each resulting couple the man and woman know each other? Perhaps only a mathematician would use the term marriage for such a situation! Yet, the theorem that gives insight into this situation is as wondrous as the experiences that lead to marriage in the real world. Here is a mathematical model which tries to frame the problem above, though it does not quite take the path followed by Hall (about which more later).
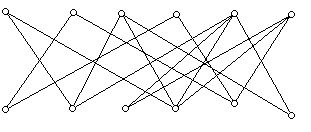
Suppose we represent the men by a collection of dots, and the women by a different collection of dots, as shown in Figure 1 below. Note that, for the moment, we need to have the same number of men and women. In the diagram shown, each man is connected to 3 women and each woman is connected to three men, there being five men (top set of dots) and five women (bottom set of dots).
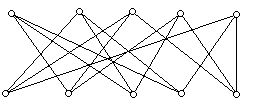
Figure 1
A more general situation occurs if we have equal numbers of men and women but we do not necessarily have the same number of women known by each man and by each woman.
Can you see why it is impossible to marry off all the men to women they know in the diagram above? (Hint: Look at the men at the far left and the far right!)
By contrast, in the diagram below, all the men can be married off to women they know.
Can you see how to pair off the men and women so that they know each other? Not a total triviality. Here is a solution:
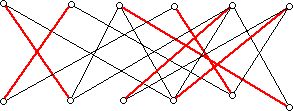
Figure 2
So, we have several issues to address here: When can one marry off the men to the women, and is there an algorithm, a simple set of rules, that can be followed, that will find such a pairing when one exists in a reasonable amount of time, even for large numbers of men and women?
The ideas that lie behind this marriage theorem were discovered independently in several different contexts. The Hungarian graph theorist Dénes König (1894-1944), the British group theorist Philip Hall and others all found their way to the circle of ideas involved.
|
|
 |
A rare photo of Dénes König, kindly provided by Filep László
|
Philip Hall
|
Hall had come across his theorem in 1935 (as a result about cosets in group theory); in recent years it is typically stated as a theorem about sets. The basic idea is to define a system of distinct representatives (SDR). Think of having a list of committees which have potentially overlapping membership. The goal is to elect a different chairperson for each committee. Abstracting, we have a collection of (unordered) sets of objects whose members have been chosen from some list M of objects. The connection with marriage theorems is that one can think of the sets as being the names that each woman lists for the men (who are the elements of the set M, which explains the use of the letter M) whom she would accept as a mate. Assigning each woman a unique man means finding an SDR for the women's sets. Hall's Theorem states that an SDR exists if and only if for any number i of the women (for i equal to one up to the total number of women) the lumping together of the men on the lists of the i women contains at least i men. (If, for example, 5 of the women only have 4 men on their lists of potential mates, no marriage assignment is possible.) The statement of Hall's Theorem, though very elegant, does not lead immediately to finding an SDR in an efficient way, it only gives a test to see if such an SDR exists. The role of an SDR in the set formulation is related to the notion of a matching in a graph. In this setting, finding an SDR becomes more practical.
A matching in a graph is a collection of edges (line segments) which have no vertex in common. Given a graph one can look for matchings which have the property that no edge can be added to the matching. Alternatively, one can look for a matching with the largest possible number of edges. A graph is said to have a perfect matching when every vertex of the graph is the endpoint of some edge in the matching. A necessary condition for this to happen is that the graph have an even number of vertices. However, graphs which have an even number of vertices need not have a perfect matching. The red lines in Figure 2 above represent a perfect matching. Interpreting the vertices as women and men shows how to marry off the women to men they know. Dénes König, who helped reenergize the study of graphs (which was first investigated by Leonard Euler), made important contributions to the theory of matchings by showing how to find matchings in an efficient manner.
Extensions of the idea of matchings allow the graph to have weights assigned to the edges. For example, one might have a collection of people and jobs for which these individuals are qualified. If personi is qualified for job j there is an edge between the vertices representing i and j. This edge can be assigned a weight which indicates:
a. The amount of time that it will take i to complete j, or
b. The efficiency with which i will be able to carry out j, or
c. The cost of completing j if i does j.
This leads to problems of matching workers to jobs to maximize something (perhaps the efficiency with which all the jobs can be completed) or minimize something (the cost of completing the jobs with a particular assignment of workers). Researchers have been successful in obtaining many theoretical and applied results for problems of this sort, including, in many cases, polynomial time (i.e. reasonably practical) algorithms for solving them.
3. Beyond the Hall Marriage Theorem
The Hall Marriage theorem aims to examine when it is possible to marry a collection of men to a collection of women who know each other. However, one can imagine that this might not be a very satisfactory situation because the people who are paired are not happy with the partners that they are assigned. A natural way to try to do better is to ask the men how they rank the women and the women how they rank the men. It is this straightforward idea that leads to a remarkable story of the interplay of theoretical and applicable ideas. The model is usually referred to as the Gale-Shapley Marriage Theorem.

David Gale

Lloyd Shapley
In fact, David Gale and Lloyd Shapley were not the first to either think of the model or apply it to a practical situation. None the less Gale and Shapley showed that there was a truly remarkable mathematical theorem that governed what happened in this situation.
Let us consider the simplest version of the Gale-Shapley framework, which has been extended in many directions, some of which I will mention. Suppose that we have two sets of equal size: a set of men and a set of women. Each man produces a ranking for each woman where indifference is not allowed. Each woman produces a ranking for each man where indifference is not allowed. For example, if the men's names are Man 1, Man 2, and Man 3; and the women's names are Woman 1, Woman 2, and Woman 3, then the rankings produced might look like:
Men's rankings of the women:
| |
1st choice
|
2nd choice |
3rd choice |
| Man 1 |
Woman 1 |
Woman 2 |
Woman 3 |
| Man 2 |
Woman 1 |
Woman 3 |
Woman 2 |
| Man 3 |
Woman 3 |
Woman 2 |
Woman 1 |
Table 1
Women's rankings of the men:
| |
1st choice |
2nd choice |
3rd choice |
| Woman 1 |
Man 2 |
Man 3 |
Man 1 |
| Woman 2 |
Man 1 |
Man 3 |
Man 2 |
| Woman 3 |
Man 3 |
Man 1 |
Man 2 |
Table 2
Our job is take these rankings and marry the men to the women, but how are we to judge when one way of pairing off the people into couples is better or worse than another way?
For example, here are some potential pairings:
Arrangement 1:
Man 1 with Woman 1
Man 2 with Woman 3
Man 3 with Woman 2
or alternatively
Arrangement 2:
Man 1 with Woman 3
Man 2 with Woman 1
Man 3 with Woman 2
In Arrangement 1, Man 1 is very content - he got his first choice. Woman 1, however, finds herself paired with her least favorite. Man 2 in this arrangement gets his second choice, he preferring Woman 1, and we have already noted that Woman 1 would prefer any of the other men to the one she was assigned. Thus, this arrangement tempts Man 2 and Woman 1 to "have an affair" because each prefers the other to the mate they were assigned. When this phenomenon happens for any man/woman pair, that pair is known as a blocking pair for the matching. If a pairing of men and women has no blocking pair, then the assignment or matching is called stable. Thus, a marriage arrangement is unstable if for some man/woman pair, that pair would prefer each other to the partners they were assigned by the arrangement.
Unfortunately, Arrangement 2 is also unstable. Man 1 and Woman 2 would prefer each other to the mates they have been assigned. Note that it may seem to be hard to find a stable matching, but given a proposed matching we can check for a given man whether or not he is a member of a blocking pair. Take Arrangement 2 above, and Man 2. Is he a member of a blocking pair? Since he was assigned Woman 1, his first choice, he can not be a member of any blocking pair. What about Man 3? He is mated with Woman 2, his second choice. Hence, we need only check if he forms a blocking pair with the woman he ranked first, namely, Woman 3. Since Woman 3 prefers Man 3 to the person she was paired with (Man 1), the two form a blocking pair.
In this example we have 6 potential ways to marry off the men to women and we can check them all to see what happens. Can you find an assignment where the stability condition holds?
The obvious question is whether for any n (at least 2), given arbitrary ranking tables for n men and n women, there is a way of marrying the men to the women in such a way that the assignment is stable.
The amazing theorem, due to Gale and Shapley, is that not only can one prove the existence of such a stable marriage assignment in all cases, but there is an algorithm that finds such a marriage assignment in a reasonable amount of time.
4. An Algorithm for Finding a Stable Marriage
How can one find a stable marriage based on the rankings that men and women produce of each other, such as Table 1 and Table 2 above?
Here is a way to find a stable matching. Imagine that each woman sits behind a desk that has been set up in a gym, with a large sign having her name on it. All the men wait until a start signal is given. When they hear this signal, each man heads off to the table of the woman whose name is highest on his list. Some women may find that several men arrive at their desk and other women that no man arrives. If a woman has several suitors, she temporarily accepts the one among them that is highest on her ranking, sending any others back to the starting line. If a woman has exactly one suitor, she temporarily accepts him. Thus, each woman who gets one or more proposals takes the best she can get at the given stage but hopes that perhaps some better (higher on her preference schedule) suitor might come along later.
In the example illustrated in Table 1 and Table 2, suppose the start signal for Round 1 is given. Men 1 and 2 head off for the desk of Woman 1 while Man 3 heads for the desk of Woman 3. Since Woman 3 has only one offer, she provisionally accepts the man who makes the offer, Man 3. (Actually, Man 3 is her first choice, so Woman 3 is very pleased to get his offer.) Woman 1, having the choice of Man 1 or 2 as suitors, provisionally accepts Man 2, and thus, Man 1 heads back to the starting line. In Round 2, when the signal is given Man 1 now goes to the next highest woman on his list who has not sent him packing previously. Thus, Man 1 next proposes at the desk of Woman 2. Since Woman 2 has no provisional suitor, she accepts Man 1, and now, since each woman has exactly one man at her desk, we have found a matching:
Woman 1 is matched with Man 2.
Woman 2 is matched with Man 1.
Woman 3 is matched with Man 3.
Often one must go through many rounds before one reaches a situation where each woman has one man at her desk. However, if one obtains a matching in this way, it is not hard to see that it must be stable.
Since the men and women are in competition with each other for highly ranked mates, it may not be clear how good or bad the stable matching we get from the procedure above is from the viewpoint of an individual man or woman. However, it turns out that the stable matching that we get when the men propose (i.e. women set up desks, and men "move around") is as good as any stable matching we can get from the point of view of each individual man, and is as bad as any stable matching can be from the point of view of each individual woman. Thus, this matching is known as the Male Optimal Stable Matching.
We could design a procedure in which we reverse the roles of the men and women: The women make proposals during the rounds of the procedure and the men set up the desks to receive proposals from them. In our example, when the signal for the start of Round 1 is heard, Woman 1 heads for Man 2's desk, Woman 2 heads for Man 1 and Woman 3 heads for Man 3's desk. The result is that each man has one suitor so we immediately get the stable matching:
Man 1 is matched with Woman 2.
Man 2 is matched with Woman 1.
Man 3 is matched with Woman 3.
Since each woman got her first choice, they are quite happy, and this stable matching is the Female Optimal Stable Matching. In fact, in this example the Male Optimal and Female Optimal Stable Matchings are identical. However, this is not always the case, as the following example shows.
| |
1st choice |
2nd choice |
3rd choice |
| Man 1 |
Woman 1 |
Woman 2 |
Woman 3 |
| Man 2 |
Woman 1 |
Woman 3 |
Woman 2 |
| Man 3 |
Woman 1 |
Woman 2 |
Woman 3 |
Table 3
| |
1st choice
|
2nd choice |
3rd choice |
| Woman 1 |
Man 2 |
Man 3 |
Man 1 |
| Woman 2 |
Man 1 |
Man 3 |
Man 2 |
| Woman 3 |
Man 2 |
Man 1 |
Man 3 |
Table 4
The Male Optimal Stable Matching is:
Woman 1 with Man 2
Woman 2 with Man 3
Woman 3 with Man 1,
while the Female Optimal Stable Matching is:
Man 1 with Woman 2
Man 2 with Woman 1
Man 3 with Woman 3.
In this case, we get two different stable matchings depending on whether the men make the proposals (Male Optimal) or the women make the proposals (Female Optimal).
One easy and clever way to extend the Gale-Shapley idea is to acknowledge that some men or women, given the collection of choices available to them, would rather be single than married to some (or perhaps all) of the mate choices. One can incorporate this idea into the ranking of a man or woman by requiring that they list themselves in the ranking of the members of the opposite sex with the understanding that, say, for a woman's ranking of the men, men to the right of her own name are people whom she would rather not marry. Thus, if Woman 2's ranking were: 1, 3, (Woman 2), 2, then Woman 2 would rank being paired with Man 1, highest, Man 3, next highest, but would prefer to be single rather than to be married to Man 2.
Similarly, if Man 3 had the ranking 1, 3, 2, (Man 3) for women, this would mean he prefers the women in the order Woman 1 first, ...., and Woman 2 lowest, but prefers even Woman 2 to remaining single. With the obvious extension of the blocking concept and stability it is possible to show that there are always stable assignments. In some of these stable assignments some men and women may not get mates. Rather amazingly, however, for any man or woman, if he or she remains single in one stable matching, then that person would remain single in all stable matchings! This remarkable theoretical result has intriguing significance in some of the many applications of the Gale-Shapley model.
5. Hospitals and Residents
When students are trained to become physicians they typically attend medical school after graduating from college. In medical school the future doctors are exposed to extensive text book learning about medicine as well as the opportunity to work with real patients. However, not surprisingly it is highly desirable that beginning doctors get extensive experience with patients before they practice medicine on a regular basis. The system of "internships" and "residencies" provides this training whereby, when doctors obtain their medical degrees from a medical school, they go through hands-on training with patients before fully completing their medical training. This creates a situation where hospitals are interested in students with various specialty interests and achievements in medical school, and students have interests in getting their training in specific hospitals. Students often show a preference for hospitals in cities or at prestigious universities rather than hospitals in rural settings.
This situation is very similar to a marriage! The hospitals want to rank the students and the students want to rank the hospitals and we want to be able to pair the students and hospitals so that no pair would rather be paired with each other than with their assigned mates. Note that hospitals often seek many students but a student can only get a position at one hospital. Much research has been done to try to find good ways of creating such matchings and addressing the social consequences of the fact that rural hospitals do not get enough students. The Gale-Shapley model, extended to the case of unacceptable partners, helps give insight into why rural hospitals do not always get the students they want.
The medical education profession had actually found its way to using a hospital ranking/student ranking matching system to pair hospitals to students and this system was in place before Gale and Shapley did their work! The descendant of this system is known today as the National Resident Matching Program (NRMP). The system that was put in place in 1952, while not explicitly stating any mathematical result in support of the system that was used, did, in fact, produce stable marriages. More importantly, the system was very successful. It brought order to a "market" that up until that time had been chaotic. What had been happening before the voluntary national clearing house system was started was that hospitals were making offers to students earlier and earlier in their medical school careers in the hopes of having the necessary future doctors they needed. As a result, these offers were being made before detailed information about student success in medical school was available and before students really knew what specialties they would pursue.
It is interesting that regional systems which developed in Great Britain to match doctors to hospitals were sometimes successful and sometimes not. In examining those regional systems that worked versus those that "fell apart" due to students working outside the system, the key turned out to be that nearly always, the systems that used algorithms which guaranteed stability for the matchings were successful, while those that were not stable did not function well. This empirical information was an interesting vindication that the "theoretical" notion of a stable matching was an important one for practical applications. The NRMP has over the years been the source of a complicated debate over which stable matching algorithm best met the collective needs of students, hospitals, and the nation. Not all of the debate centered around the matching aspects of the process. Some claimed that the system violated anti-trust laws by allowing hospitals to get a cheap source of qualified "laborers."
Alvin Roth (now at Harvard University) has been a pioneer in exploring the economic implications of two-sided matching markets (in particular the NRMP) and in exploring how to design systems such that they are well accepted. By clarifying how the system has worked in practice and providing detailed nuances of the goals of the students and hospitals, Roth has tried to make the NRMP work better.
Mathematics often progresses by simplifying a situation down to its skeletal essence and in this form getting a striking theorem, one like the Gale-Shapely Marriage Theorem or the Hall Marriage Theorem. However, once one has a spectacular result of this kind it becomes common to try to extend the domain of the theorems to different but related territory. As the system for pairing hospitals and interns evolved, strains developed in the system. One strain was that many doctors married (!) in medical school. Naturally, these couples wanted to be assigned to the same hospital or at the very least to a hospital in the same or nearby city. However, it might well happen that hospitals did not have equal interest in the two married people, who might have rather different appeal (i.e. one might have been a much better student than the other). This problem with meeting the needs of married students has resulted in a rising level of medical school graduates who have chosen not to work through the NRMP. Unfortunately, it is known that trying to extend the Gale-Shapley Theorem to a model that incorporates dealing with "pairs" can not always be guaranteed to provide a stable matching in all situations.
A nice example of this is another attempt to extend the idea of pairings, present in both the Hall Theorem and the Gale-Shapley Theorem. Again one has 2n people, but this time, instead of having two sexes and wanting to marry off men and women, the 2n people are perhaps of the same sex. Think of the people being paired for the purpose of making them roommates. In this case each of the 2n people rates all the other people, and again one wants to pair off the people so that the assignment of roommate pairs is stable. In this case it is not that hard to find examples where there is no stable matching. Negative results of this kind, where examples show there is no general theorem, rarely put mathematicians off. The new challenge is to find what additional special conditions on the rankings produced allow one to find a stable matching.
Joseph Malkevitch
York College (CUNY)
malkevitch at york.cuny.edu 
6. References
Adachi, Hiroyuki. On a characterization of stable matchings. Econom. Lett. 68 (2000), no. 1, 43--49. MR1765147 (2001e:91128)
Aldershof, Brian; Carducci, Olivia M. Stable matchings with couples. Discrete Appl. Math. 68 (1996), no. 1-2, 203--207. MR1393319 (97a:05011)
Alkan, Ahmet. A class of multipartner matching markets with a strong lattice structure. Econom. Theory 19 (2002), no. 4, 737--746. MR1906928 (2003d:91072)
Balinski, Michel; Ratier, Guillaume . On stable marriages and graphs, and strategy and polytopes. SIAM Rev. 39 (1997), no. 4, 575--604. MR1491048 (99b:90096)
Blair, Charles. Every finite distributive lattice is a set of stable matchings. J. Combin. Theory Ser. A 37 (1984), no. 3, 353--356. MR0769224 (86d:05032)
Blair, Charles. The lattice structure of the set of stable matchings with multiple partners. Math. Oper. Res. 13 (1988), no. 4, 619--628. MR0971914 (90c:90005)
Colenbrander, A., Match algorithms revisited, Academic Medicine, 71 (1996) 414-415.
Crawford, V. and E. Knoer, Job matching with heterogeneous firms and workers, Econometrica 49 (1981) 437-450.
Demange, Gabrielle; Gale, David ; Sotomayor, Marilda . A further note on the stable matching problem. Discrete Appl. Math. 16 (1987), no. 3, 217--222. MR0878022 (88c:90161)
Feder, Tomás. A new fixed point approach for stable networks and stable marriages. Twenty-first Symposium on the Theory of Computing (Seattle, WA, 1989). J. Comput. System Sci. 45 (1992), no. 2, 233--284. MR1186885 (93j:68154)
Gale, David. The two-sided matching problem. Origin, development and current issues. Special issue on operations research and game theory with economic and industrial applications (Chennai, 2000). Int. Game Theory Rev. 3 (2001), no. 2-3, 237--252. MR1855134 (2002g:91004)
Gale, D. and L. Shapley, College admissions and the stability of marriage, Amer. Math. Monthly, 69 (1962) 9-15.
Gale, David; Sotomayor, Marilda . Ms. Machiavelli and the stable matching problem. Amer. Math. Monthly 92 (1985), no. 4, 261--268. MR0786525 (87g:90133)
Gale, David; Sotomayor, Marilda . Some remarks on the stable matching problem. Discrete Appl. Math. 11 (1985), no. 3, 223--232. MR0792890 (87g:90069)
Gusfield, Dan; Irving, Robert W. The stable marriage problem: structure and algorithms. Foundations of Computing Series. MIT Press, Cambridge, MA, 1989. xviii+240 pp. ISBN: 0-262-07118-5 MR1021242 (91e:68062)
Gusfield, Dan; Irving, Robert ; Leather, Paul ; Saks, Michael . Every finite distributive lattice is a set of stable matchings for a small stable marriage instance. J. Combin. Theory Ser. A 44 (1987), no. 2, 304--309. MR0879688 (88c:06022)
Roth, Alvin E.; Sotomayor, Marilda . Interior points in the core of two-sided matching markets. J. Econom. Theory 45 (1988), no. 1, 85--101. MR0949070 (90f:90034)
Knuth, D., Marirages Stables, Les Presses de l’Université de Montreal, Montréal, l976.
Knuth, Donald E. Stable marriage and its relation to other combinatorial problems. An introduction to the mathematical analysis of algorithms. Translated from the French by Martin Goldstein and revised by the author. CRM Proceedings & Lecture Notes, 10. American Mathematical Society, Providence, RI, 1997. xiv+74 pp. ISBN: 0-8218-0603-3 MR1415126 (97h:68048)
Maffray, Frédéric. Kernels in perfect line-graphs. J. Combin. Theory Ser. B 55 (1992), no. 1, 1--8. MR1159851 (93i:05061)
McVitie, D. G.; Wilson, L. B. The stable marriage problem. Comm. ACM 14 (1971), 486--490. MR0307688 (46 #6808)
Mongell, S. and A. Roth, Sorority rush as a two-sided matching mechanism, Amer. Economic Rev., 81 (1991) 441-464.
Roth, Alvin E. The economics of matching: stability and incentives. Math. Oper. Res. 7 (1982), no. 4, 617--628. MR0686535 (84f:90008)
Roth, A., The evolution of the labor market for medical interns and residents: A case study in game theory, J. of Political Economy, 92 (1984) 991-1016.
Roth, Alvin E. The college admissions problem is not equivalent to the marriage problem. J. Econom. Theory 36 (1985), no. 2, 277--288. MR0804897 (87h:90013)
Roth, Alvin E. On the allocation of residents to rural hospitals: a general property of two-sided matching markets. Econometrica 54 (1986), no. 2, 425--427. MR0832765 (87i:05038)
Roth, A. and U. Rothblum, Truncation strategies in Matching Markets: in search of practical advice for participants, Econometrica, 67 (1999) 21-43.
Roth, Alvin E.; Sotomayor, Marilda . The college admissions problem revisited. Econometrica 57 (1989), no. 3, 559--570. MR0999272 (91a:90196a)
Roth, Alvin E.; Sotomayor, Marilda A. Oliveira . Two-sided matching. A study in game-theoretic modeling and analysis. With a foreword by Robert Aumann. Econometric Society Monographs, 18. Cambridge University Press, Cambridge, 1990. xiv+265 pp. ISBN: 0-521-39015-X MR1119308 (93b:90001)
Roth, Alvin E.; Vande Vate, John H. Random paths to stability in two-sided matching. Econometrica 58 (1990), no. 6, 1475--1480. MR1080814
Roth, Alvin E.; Vande Vate, John H. Incentives in two-sided matching with random stable mechanisms. Econom. Theory 1 (1991), no. 1, 31--44. MR1095152 (92a:90026)
Rothblum, Uriel G. Characterization of stable matchings as extreme points of a polytope. Math. Programming 54 (1992), no. 1, Ser. A, 57--67. MR1158813 (93c:90065)
Teo, Chung-Piaw; Sethuraman, Jay . The geometry of fractional stable matchings and its applications. Math. Oper. Res. 23 (1998), no. 4, 874--891. MR1662426 (99k:90140)
Vande Vate, John H. Linear programming brings marital bliss. Oper. Res. Lett. 8 (1989), no. 3, 147--153. MR1007271 (90g:90132)
Williams, K., A reexamination of the NRMP Matching Algorithm, Academic Medicine, 70 (1995) 470-476.
NOTE: Those who can access JSTOR can find some of the papers mentioned above there. For those with access, the American Mathematical Society's MathSciNet can be used to get additional bibliographic information and reviews of some these materials. Some of the items above can be accessed via the ACM Portal, which also provides bibliographic services.