Feature Column from the AMS

Matroids: The Value of Abstraction

5. Applications of matroids

One application of the unifying concept of a matroid is to find the analogs of an interesting idea in vector spaces to graphs and conversely. However, are there applications of this idea to areas outside of mathematics? Here are two examples where the applicability of ideas in graph theory has used the more abstract setting of matroid theory to find a wider range of insights.

Consider a collection of jobs that has to be filled by some collection of workers. For each job there is a list of workers (whose names in this example are 1,2,...,7) who are qualified to perform that job. The problem is to determine if it is possible to assign a qualified worker to each job. Here is a specific example, where in fact each worker can be assigned a job for which he/she is qualified:

J₁ =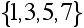

J₂ =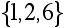

J₃ =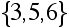

J₄ =

J₅ =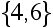

J₆ =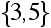

J₇ =

This particular problem can be answered by a theorem of the British mathematician Philip Hall (1904-1982), who is shown below:

Hall's Theorem states that given a collection of subsets of a finite set, it is possible to select one element from each of these sets so that the chosen elements are distinct if and only if the union of any k of the sets has at least k elements.

The chosen elements are sometimes referred to as a system of distinct representatives (SDR). Hall's Theorem has similar counterparts in other branches of combinatorics and shows up in matroid theory in the guise of transversal matroids. It was Richard Rado who helped show the special role that Hall's Theorem has for matroids. This has led to the subfield within matroids of the study of transversal matroids.

Unfortunately, there are many approaches to finding which workers to assign to which jobs, and Hall's Theorem does not provide a practical test for finding such an assignment. Furthermore, there are many variations of the problem: For example, one might want to have a rating for the quality of each worker's performance on a particular job. Now find the assignment of workers to jobs such that the minimum rating of any worker assigned to a job is maximized, or find the assignment of workers to jobs where the sum of the ratings for the workers assigned to jobs is maximized.

Another application of ideas related to matroids is provided by the following example.

Suppose the graph below with weights attached to the edges gives the cost of providing a special type of wireless communication between A, B, C, D, and E. The cost of being able to send a message between two sites located at the endpoints of the edge is given by the weight assigned to that edge.

Although each pair of vertices in this graph is linked, in general we do not need links between any pair of vertices, because vertices connected indirectly can have messages relayed between them. Thus, if there are links from B to C and C to E, then a message can be sent from B to E even though the edge BE is not part of the system. What edges should be placed into the network so that messages can be sent between any pair of the 5 locales and so that the cost of providing the service is a minimum? What is required is that one find aminimum weight spanning tree for the graph.

The American mathematician Joseph Kruskal (1956) is usually given credit for finding a very elegant solution to this problem, though in fact the solution was published (in Czech) somewhat earlier by the Czech mathematician Boruvka in 1926. The Kruskal-Boruvka algorithm is a greedy algorithm in that at each stage a local best decision is made. Here is the procedure. Sort the weights of the edges from smallest to largest. At each stage select that edge which is cheapest (ties can be broken arbitrarily), which taken together with previous chosen edges, does not create a circuit.

Clearly it makes no sense to create a circuit because given the fact that messages can be relayed, one can still send messages between any pair of vertices which make up the circuit by omitting the most expensive edge in the circuit. It requires proof, however, that the tree that results from this procedure has as cheap a cost as possible. If you have ever tried to minimize the distance that you drive to run a series of errands and done so by driving by the closest location you have not yet visited before returning home, you probably know that making a greedy choice is not always the best!

Where matroids come in is that using matroid theory, one can determine exactly the conditions under which a greedy procedure such as the one described here can be carried out successfully. This allows a quick identification of the possibility of solving a particular problem by a greedy algorithm via use of the matroid concept.

As more and more insights have been obtained into matroids in general, more insight has been obtained into all the classes of matroids. As new properties of specific types of matroids have been uncovered, attempts to find the analogs for other types of matroids have been made. By doing this mathematics and its applications continue to grow.