Mathematical Card Tricks
6. It's probably magic
Bearing in mind the unavoidable possibility that a trick which is known to be mathematically watertight can go wrong -- either the magician or a victim can make a mistake and cause the whole effect to blow up in your face -- it's as well to be prepared for emergencies and keep a short, snappy crowd pleaser in reserve that you know cannot fail. It's also worth considering tricks that merely have a high probability of working. Even if mathematics cannot guarantee 100% success every time, the payoffs when the tricks do work arguably outweigh the red faces on the rare occasions when they don't. If the dice seem to be against you on the day that you try one of these in public, simply act as you do when one of your old reliable tricks lets you down, and say nothing to make your audience think this trick is any different from the rest.
This brings us to one of the most startling prediction tricks imaginable.




















The Kruskal Count
Effect: The victim shuffles a deck thoroughly, then secretly picks a number between 1 and 10. The cards are dealt out slowly and steadily, face up, the victim's first key card being the one at the position they choose in advance. The value of this card determines how many to deal out to the next key card, e.g., if the key card is a 4 victim counts off four cards, the last being the new key card. Royal cards count 5. The process is repeated as often as is possible. Eventually they will get a key card (perhaps the last card in the deck) which is not followed by enough cards to get to another one; this last key card is the one they remember. No matter how steadily the victim deals, with no pauses to give any hints as to which cards are key cards, you successfully identify their last key card. For many people, this trick grows more mysterious with repetition.
Method: The method is simple: you yourself follow the same instructions as the victim deals off the cards, picking at random some card among the first ten, and so on, finally arriving at your own last key card. The amazing thing is that with very high probability you'll both have come to the same final key card. In fact, your apparantly independently determined streams will most often flow together somewhere along the way, sometimes before you are even half way through the deck!
We advise you to run through a full demonstration of the counting procedure for the victim, pausing at each key card for clarity, before you let them loose with the deck (don't forget to shuffle it first!).
Here is one possible ordering of the deck:












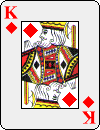





















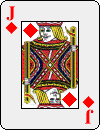

















Of the ten choices available for the first key card, the first nine lead to the 3 of Spades as the final key card: only the tenth, the 10 of Spades, leads to the 10 of Diamonds instead. Even more surprising is how soon most of the streams come together: seven of them converge at the 9 of Clubs in the third row.
Mathematics: The principle at work here can be explained in terms of Markov processes, and was discovered by Princeton physicist Martin Kruskal. We recommend an online discussion of the mathematics and a computer simulation, both related to the paper ``On Kruskal's Principle'' by Wayne Haga & Sinai Robins (from Organic Mathematics (Burnaby, BC, 1995), Canadian Math Society Conference Proceedings 20 (AMS, 1997).
Here is a heuristic argument suggested by Tony Phillips which sheds some light on the phenomenon: ``There is a 0.1 chance of the magician picking the same first card as the victim. That first card is number 5.5 on the average. Counting the royal cards as 5, the average length of subsequent steps is (1+2+...+10+5+5+5)/13=5.38, so the density of the victim's key cards can be expected to be 1/5.38=0.186. Similarly, the magician can be expected to choose 8 key cards after the first, since (52-5.5)/5.38=8.64. Each of these cards has 0.186 chance of being one of the victim's key cards, and 1-0.186=0.814 chance of missing. The probability of the magician not hitting one of the victim's key cards on the first or on any of the later choices is therefore 0.9x(0.814)8=0.174, so the probability of a win for the magician, by this rough estimate, is 0.826.''
Source: This one was first learned from Gardner's Penrose Tiles to Trapdoor Ciphers (W.H. Freeman & Co, 1989).
Bonus points: Another possibility which increases the chance of success, which was pointed out to us by Gordon Bean, is to spell out one card for the each letter in the name of key cards, so that, for instance, ``ten'' advances three cards (``T-E-N''). A word of caution, however: spelling values on this scale is risky, as it's so easy for one or both of you to get confused and revert to ordinary counting.
The implications of this trick are very interesting: are some apparently unrelated chains of unfolding events doomed to lock together in sync after a while? See ``An old card trick and new Biblical hoax'' -- excerpted from Once Upon a Number - The Hidden Mathematical Logic of Stories (Basic Books, 1998) by John Allen Paulos, for musings along these lines.
It takes patience and care on the part of two people for this phenomenon to be demonstrated correctly: that you and your victim can float merrily downstream, oblivious to each other's progress, only to discover (with high proability) that you are on tributaries of the same river. That being the case, may we recommend playing some appropriately aquatic music, such as Smetana's Ultava -- an orchestral tone poem which follows the course of a river from mountain streams to its inevitable destination -- as you await the harmonious confluence!
Revised 10/26/00






















































