Feature Column from the AMS

Oriented Matroids: The Power of Unification

2. Digraphs and oriented matroids

Intuitively, a graph can be thought of as a collection of points joined by a collection of lines. Two graphs are considered the same or isomorphic if the elements of the graph are joined in the same way. Thus, the two graphs below look different but are isomorphic.

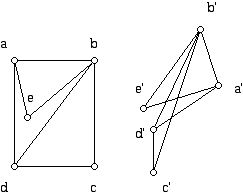
The function (association scheme) between the vertices necessary to see that the structures are the same matches a vertex named x with one named x'. Two vertices x and y are joined by an edge if and only if x' and y' are joined by an edge.

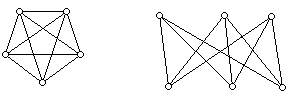
Though often the definition of a graph has a "set theory" (abstract) flavor, the graph concept quickly takes on a geometrical feel in diagrams such as the one above. Furthermore, geometric issues quickly come to the fore when one thinks of the points as being drawn on a surface, usually the plane, and asks that the line segments that join the vertices intersect only at vertices. Note that the graphs below can not be drawn in the plane or on the sphere so that the line segments meet only at vertices, but both graphs can be so drawn on the torus (donut).

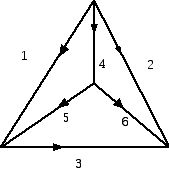
One can think of digraphs in a "set theory" framework or as related to graphs. Instead of taking twovertices and joining them by an "undirected" edge, one thinks of an arrow pointing along an edge from one vertex to another. (Structureswith dots and lines where some edges are undirected and some are directed areknown as mixed graphs.) In the digraph below each directed edge has been assigneda number. What is special about this digraph is that you can not move along edges,following the arrows in their indicated directions, and return to where you started.If we assign a direction for each of the "cycles" in the graph withoutthe arrows, we can state for each edge of such a cycle whether it is consistentwith the direction which the cycle has in the digraph. When the direction isconsistent, we call the edge positive. Otherwise it is called negative.

Thus, for the "cycle" of edges 4, 5, 3, 2, 4 we have that 4, 5 and 3 are positive but 2 is negative, while for the cycle 1, 5, 6, 2, 1 we have that 1 and 6 are positive while 5 and 2 are negative. Thus, for each of the "underlying" cycles in the graph one gets a signed circuit for the digraph. The oriented matroid associated with this digraph is defined in terms of an edge set and a collection of signed circuits, analogous to the edge set and circuits of a matroid. The goal of this article is not to pursue the details of the many axiomatizations for oriented matroids, but rather to call attention to some of the disparate geometric phenomena that are explored in thinking about oriented matroids and the various guises they come in.