Feature Column from the AMS

Oriented Matroids: The Power of Unification

5. Allowable sequences

Often in the discussion of new ideas, new inventions, and new technologies, the distinction between incremental improvements versus true "revolutions" is made. True revolutions are rare. Nearly always, something new is inspired by something old and extends some aspect of the old ideas in a new direction. Thus, allowing multiple edges and/or loops in a "graph" extends the idea of a (simple) graph. Two schools have developed with regard to defining graphs so as to allow multiple edges and loops or not. There are pros and cons to either approach. Digraphs can be thought of as an extension of the graph concept. It is subtle distinctions of this kind that intrigue mathematicians and drive math skeptics nuts! There are statements which are true of simple graphs but are not true of graphs with multiple edges. In the discussion below we see the complex way that previously explored concepts are put to work for the purpose of generating new ideas and making progress on problems that have eluded solution with previously explored ideas.

A tenacious problem in dealing with configurations of points and lines has been finding a good way of determining when two such configurations are the same or different. What is involved here is a collection of points (the points are labeled) at various locations in a plane. The set of 5 planar points below will serve as an example.

Here is another configuration of 5 labeled points:

Are these two configurations of points the same or different?

For a graph we saw above that two graphs can look rather different, yet be isomorphic or have the same structure. Take the two-point configurations and add some of the line segments between them. We obtain the two graphs below:

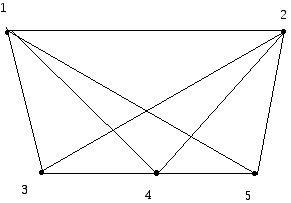
A graph constructed from the first point configuration

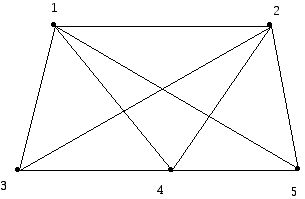
A graph constructed from the second point configuration

The diagrams above were obtained from the original two-point configurations by joining any two vertices that determine a line with a line segment. Since 5 points determine 10 lines, we might have 10 edges in the resulting graphs but we have chosen not to have an edge in diagrams for the line segments from the vertices labeled 3 and 5, because these segments would "lie on top of" segments joining other vertices. Notice that as graphs, these two graphs are isomorphic. (They would still be isomorphic if we had included edges between the vertices 3 and 5.) However, can you make a case for why the two original point configurations might be said to be different, even though the constructed graphs were the same?

To get at a concept of equivalence or inequivalence of point configurations that goes beyond the construction of associated graphs, let us consider the ingenious approach below, developed by Jacob Eli Goodman (City College, City University of New York) and Richard Pollack (Courant Institute of Mathematical Sciences, NYU).

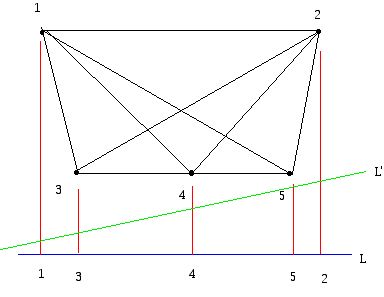
A diagram to illustrate the concept of allowable sequences

If we take the point configuration above and project (using the red lines) its labeled vertices onto the blue line L, we obtain points in the order 13452. As we rotate the line L into other positions in a counterclockwise direction, we reach a location where there is a pair of points in the original configuration which for the first time determine a line whose direction is perpendicular to the rotating line. If we rotate just a bit further (to the green line L') and project the points onto this line, the order of the points 1 and 3 will reverse and we obtain the permutation 31452. Rotating further for the above configuration and making switches as they are encountered, we get the new permutation 34152, and then 34512, 54321 (note for this position we get two switches of numbers simultaneously because there are two parallel lines in the configuration), 54231, 52431, and 25431. At this point we have rotated the original line through 180 degrees. The permutation is exactly the reverse of what it was originally. We can now continue our rotation until we get back to the original position for the rotating line, and arrive at the original permutation 31452. Notice that we can code the way one obtains the next permutation in the sequence by the "section(s)" of the previous permutation that must be flipped to obtain the next permutation. The sequence of permutations that is obtained from the point configuration in this way is called an allowable sequence by Goodman and Pollack. What has been accomplished is to capture information about the point configuration in terms of "algebra." A collection of permutations on the symbols 1,..., n, starting and ending with the same permutation, is called allowable if:

a. The way one gets from one permutation to the next is to switch (reverse) one or more sets of non-overlapping strings of consecutive symbols

b. After a move in which symbols i and j switch, they do not switch again until every other pair has switched

c. All the symbols do not switch simultaneously.

(Condition (c) means that in terms of point configurations we do not permit all the points to be on one line.)

Allowable sequences provide a tool for telling when the point configurations are "inequivalent" because the allowable sequences are inequivalent. Using these ideas and other ideas developed by Goodman and Pollack (the order type of a configuration), O. Aichholzer, F. Aurenhammer, and H. Krasser were able to show that there are 14,309,547 inequivalent (suitably defined) ten-point configurations! (As you might guess, they used a computer to help with the enumeration.)

Although point configurations give rise to allowable sequences, it does not follow that every allowable sequence comes from a geometric configuration of points. In fact, it turns out that there are allowable sequences that do not arise from configurations of points.

Goodman and Pollack realized that one could also develop allowable sequences in the framework of the points determined from a given configuration of lines, rather than the approach developed above, where we looked at the lines determined from a configuration of points. This approach followed the "duality" between points and lines that plays an important role in the geometry of a projective plane. They further extended their ideas connecting the notion of allowable sequences from lines to pseudolines and point configurations, to a more general notion of generalized configuration of points. The generalized configurations of points play a similar role for point configurations that pseudolines do for line configurations. Additionally, they looked into how to extend their work to point configurations in higher dimensional spaces.

It was a sign of the fact that Goodman and Pollack had important ideas that shortly after their work introducing the ideas of allowable sequences, another mathematician, Peter Ungar (who at the time was at the Courant Institute), showed how to use allowable sequences to solve a question that had been unresolved for many years. Ungar answered a question of P. Scott's that seems so easy, it's hard to imagine that it was not resolved much earlier.

Suppose one has n points in the plane not all on a straight line. It is not difficult to see that these points can determine many directions. (Those familiar with the concept of the slope of a line can think of the directions determined by pairs of points as being given in terms of the slopes of the associated lines.) For example, the 4 points below determine 6 different directions. Six is the maximum number of different directions that 4 points can determine. More generally, n points can determine a maximum of n(n-1)/2 different directions.

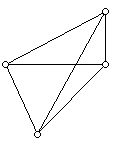
However, what happens at the other extreme? How few directions can be determined by planar configurations of points (not all on a line)? The rectangular configuration of points below determines only 4 different directions:

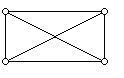
The two intersecting diagonals have different directions and there are pairs of points which determine vertical and horizontal lines, giving a total of 4 directions. No configuration of 4 points (not all on a line) can determine fewer directions. Scott conjectured that for n points not all on a line (n ≥ 4), the fewest number of directions is 2s when n has the form 2s (i.e. n is even) and 2s when n has the form 2s+1 (i.e. n is odd). Much work has been done by Robert Jamison (Clemson University) on determining those configurations for which the minimum number of directions can occur. Some infinite classes are known, as well as many sporadic configurations.

Using an extremely appealing argument based on allowable sequence ideas, Ungar proved Scott's conjecture. Allowable sequences and Ungar's proof have turned out, as is so often the case in mathematics, to open up new problems, proof techniques, and further new ideas.